序列搜索策略包括贪心搜索、穷举搜索和束搜索。
贪心搜索所选取序列的计算量最小,但精度相对较低。
穷举搜索所选取序列的精度最高,但计算量最大。
束搜索通过灵活选择束宽,在正确率和计算代价之间进行权衡。
在序列到序列学习(seq2seq,BLEU)_流萤数点的博客-CSDN博客中,我们逐个预测输出序列, 直到预测序列中出现特定的序列结束词元“<eos>”。 本节将首先介绍贪心搜索(greedy search)策略, 并探讨其存在的问题,然后对比其他替代策略: 穷举搜索(exhaustive search)和束搜索(beam search)。

1.贪心搜索
首先,让我们看看一个简单的策略:贪心搜索, 该策略已用于 9.7节的序列预测。 对于输出序列的每一时间步t′, 我们都将基于贪心搜索从Y中找到具有最高条件概率的词元,即:

一旦输出序列包含了“<eos>”或者达到其最大长度T′,则输出完成。
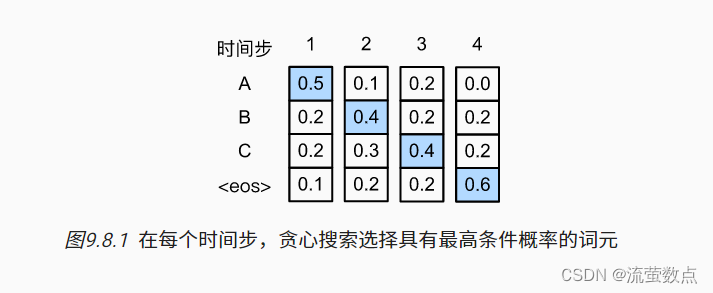
如 图9.8.1中, 假设输出中有四个词元“A”“B”“C”和“<eos>”。 每个时间步下的四个数字分别表示在该时间步 生成“A”“B”“C”和“<eos>”的条件概率。 在每个时间步,贪心搜索选择具有最高条件概率的词元。 因此,将在 图9.8.1中 预测输出序列“A”“B”“C”和“<eos>”。 这个输出序列的条件概率是 0.5×0.4×0.4×0.6=0.048。

然而,贪心搜索无法保证得到最优序列。
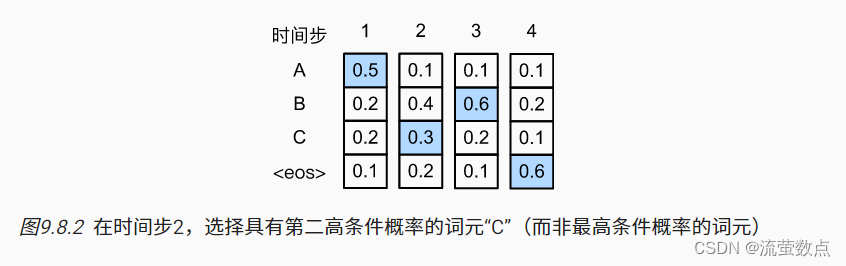
图9.8.2中的另一个例子阐述了这个问题。 与 图9.8.1不同,在时间步2中, 我们选择 图9.8.2中的词元“C”, 它具有第二高的条件概率。 由于时间步3所基于的时间步1和2处的输出子序列已从 图9.8.1中的“A”和“B”改变为 图9.8.2中的“A”和“C”, 因此时间步3处的每个词元的条件概率也在 图9.8.2中改变。 假设我们在时间步3选择词元“B”, 于是当前的时间步4基于前三个时间步的输出子序列“A”“C”和“B”为条件, 这与 图9.8.1中的“A”“B”和“C”不同。 因此,在 图9.8.2中的时间步4生成 每个词元的条件概率也不同于 图9.8.1中的条件概率。 结果, 图9.8.2中的输出序列 “A”“C”“B”和“<eos>”的条件概率为 0.5×0.3×0.6×0.6=0.054, 这大于 图9.8.1中的贪心搜索的条件概率。 这个例子说明:贪心搜索获得的输出序列 “A”“B”“C”和“<eos>” 不一定是最佳序列。
2.穷举搜索
如果目标是获得最优序列, 我们可以考虑使用穷举搜索(exhaustive search): 穷举地列举所有可能的输出序列及其条件概率, 然后计算输出条件概率最高的一个。
虽然我们可以使用穷举搜索来获得最优序列, 但其计算量O()可能高的惊人。 例如,当|Y|=10000和T′=10时, 我们需要评估
=
序列, 这是一个极大的数,现有的计算机几乎不可能计算它。 然而,贪心搜索的计算量 O(|Y|T′) 通它要显著地小于穷举搜索。 例如,当|Y|=10000和T′=10时, 我们只需要评估10000×10=
个序列。
3.束搜索
那么该选取哪种序列搜索策略呢? 如果精度最重要,则显然是穷举搜索。 如果计算成本最重要,则显然是贪心搜索。 而束搜索的实际应用则介于这两个极端之间。
束搜索(beam search)是贪心搜索的一个改进版本。 它有一个超参数,名为束宽(beam size)k。 在时间步1,我们选择具有最高条件概率的k个词元。 这k个词元将分别是k个候选输出序列的第一个词元。 在随后的每个时间步,基于上一时间步的k个候选输出序列, 我们将继续从k|Y|个可能的选择中 挑出具有最高条件概率的k个候选输出序列。
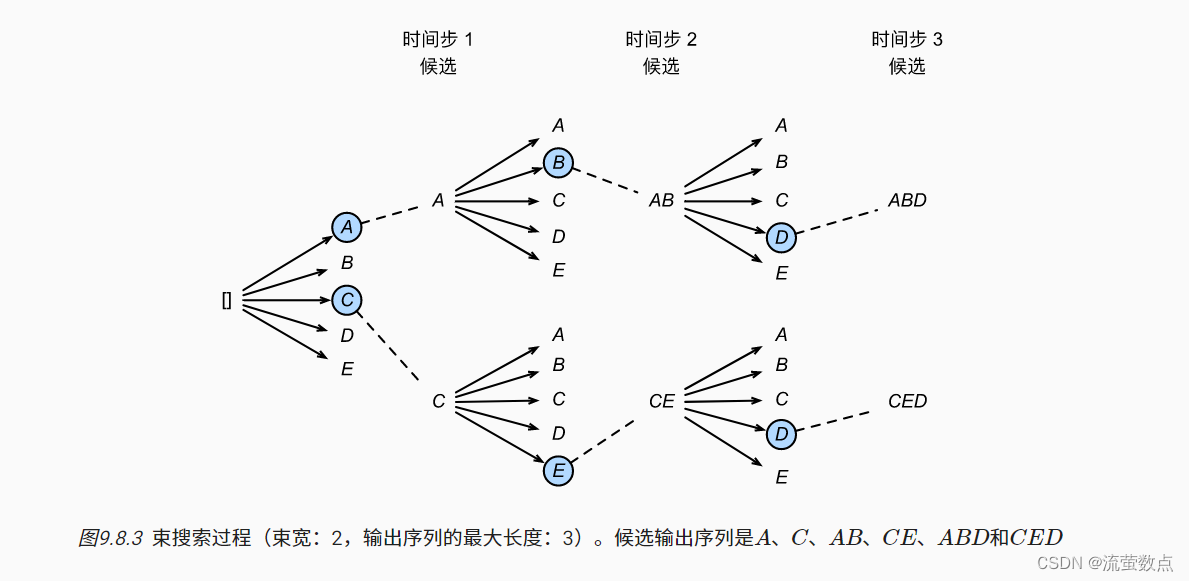
图9.8.3演示了束搜索的过程。 假设输出的词表只包含五个元素: Y={A,B,C,D,E}, 其中有一个是“<eos>”。 设置束宽为2,输出序列的最大长度为3。 在时间步1,假设具有最高条件概率 P(y1∣c)的词元是A和C。 在时间步2,我们计算所有y2∈Y为:

从这十个值中选择最大的两个, 比如P(A,B∣c)和P(C,E∣c)。 然后在时间步3,我们计算所有y3∈Y为:
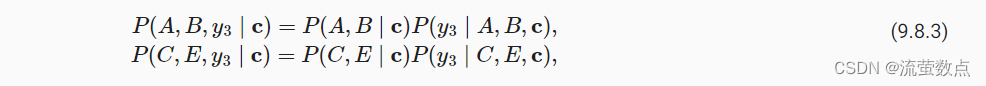
从这十个值中选择最大的两个, 即P(A,B,D∣c)和P(C,E,D∣c), 我们会得到六个候选输出序列: (1)A;(2)C;(3)A,B;(4)C,E;(5)A,B,D;(6)C,E,D。
最后,基于这六个序列(例如,丢弃包括“<eos>”和之后的部分), 我们获得最终候选输出序列集合。 然后我们选择其中条件概率乘积最高的序列作为输出序列:
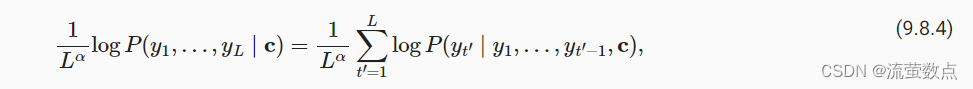
其中L是最终候选序列的长度, α通常设置为0.75。 因为一个较长的序列在 (9.8.4) 的求和中会有更多的对数项, 因此分母中的用于惩罚长序列。
束搜索的计算量为O(k|Y|T′), 这个结果介于贪心搜索和穷举搜索之间。 实际上,贪心搜索可以看作一种束宽为1的特殊类型的束搜索。 通过灵活地选择束宽,束搜索可以在正确率和计算代价之间进行权衡。