遍历

遍历

• 即:遍历每个元素。
  for遍历只会遍历每个元素一次。
  二叉树遍历每个元素则会依次遍历三次。
  分别叫
  第一次，前序，即通过父节点进入此节点
  第二次，中序，即通过左节点进入此节点
  第三次，后序，即通过右节点进入此节点
  而通过左右节点进入则代表左右子树都遍历完。

中序遍历/节点的中序

void traveres(TreeNode* root){

        if(!root)
            return;

        traveres(root->left);

        cout << root->val << endl;

        traveres(root->right);
    }

中序遍历亦叫节点的中序。即节点在中序的时候做cout。而遍历也就是每个节点都在中序的时候做cout。
所以traveres(root->left);指节点的左树都做中序，即左树的中序。所以，cout会在节点的左树中序后执行。
所以，中序遍历的时机就是遍历完左树后。
所以，节点的中序 = 左树的中序 + 节点。
节点的全部中序 = 节点左树中序 + 节点 + 节点右树中序。
但在节点中序前(cout前)也是有其内容的，那么这些内容是什么。
这些内容就是节点与根节点路径上的节点中序。但并非每个节点都有中序。而是要具体判断。
如13中序前(cout前)，
13左树中序(无13(因为指的是cout前))，6+6左树的中序，无3，1+1左树的中序。
判断方式:
是否遍历完节点左树。即节点中序。而左树的结果也就是左树中序。

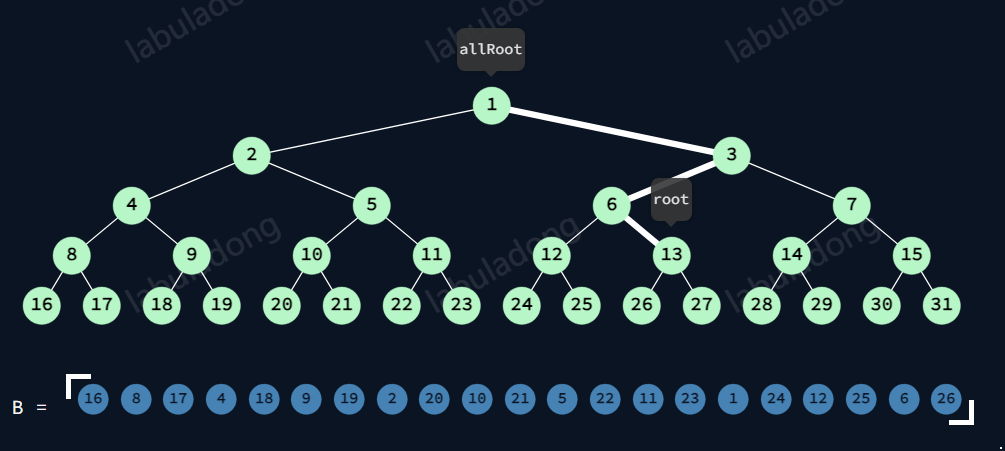
前序遍历-节点的前序

void traveres(TreeNode* root){

        if(!root)
            return;
        
        cout << root->val << endl;

        traveres(root->left);
        traveres(root->right);
    }

节点在前序比较简单，即指在第一次进节点时做cout。
同理，traveres(root->left);则指左树的前序。
当然，节点前序前也并非什么都没有，而是有其与根节点的路径上的节点。但此时路径上的节点则必有。
如14，有7的前序，有3的前序，有1的前序。

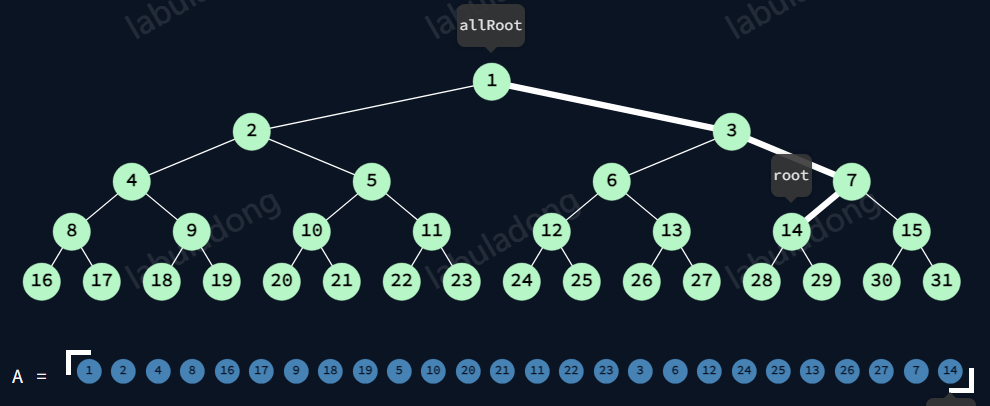
后序遍历-节点的后序

void traveres(TreeNode* root){

        if(!root)
            return;
        
        traveres(root->left);
        traveres(root->right);

        cout << root->val << endl;
    }

后序遍历指节点在后序时做cout。所以，每个节点都在后序时做cout。
即，traveres(root->left);指左树的后序。
所以，后序遍历的具体时间点就是在左树和右树的后序后。
即，节点的后序 = 左树的后序 + 右树的后序 + 根节点。
当然，节点的后序前也并非什么都没有。但此时路径上的节点则必没有。
如15，则有14的后序，有6的后序，有2的后序。

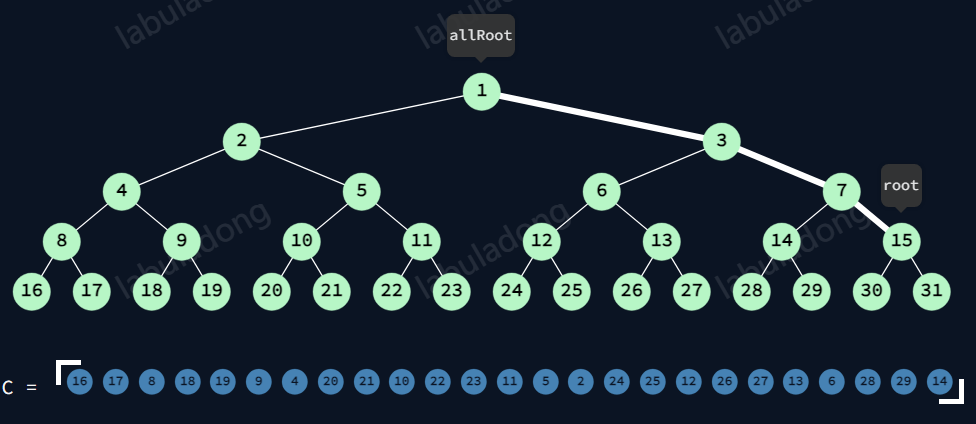
三序综合

    vector<int> A;
    vector<int> B;
    vector<int> C;

    void traveres(TreeNode* root){

        if(!root)
            return;
            
        A.push_back(root->val);
        
        traveres(root->left);
        
        B.push_back(root->val);
        
        traveres(root->right);

        C.push_back(root->val);
    }

任意一个节点
如13

13-Apush前/前序前

此时
前序结果:
6+6左树的前序，3，1+1左树的前序。路径节点必有。
中序结果:
6+6左树的中序，无3，1+1左树的中序。具体判断。
后序结果:
12的后序，2的后序。路径的节点必无。

13-Bpush前/中序前

此时
前序结果:
13+13左树的前序，6+6左树的前序，3，1+1左树的前序。路径节点必有。
中序结果:
13左树的中序，6+6左树的中序，无3，1+1左树的中序。具体判断。
后序结果:
13左树的后序，12的后序，2的后序。路径的节点必无。

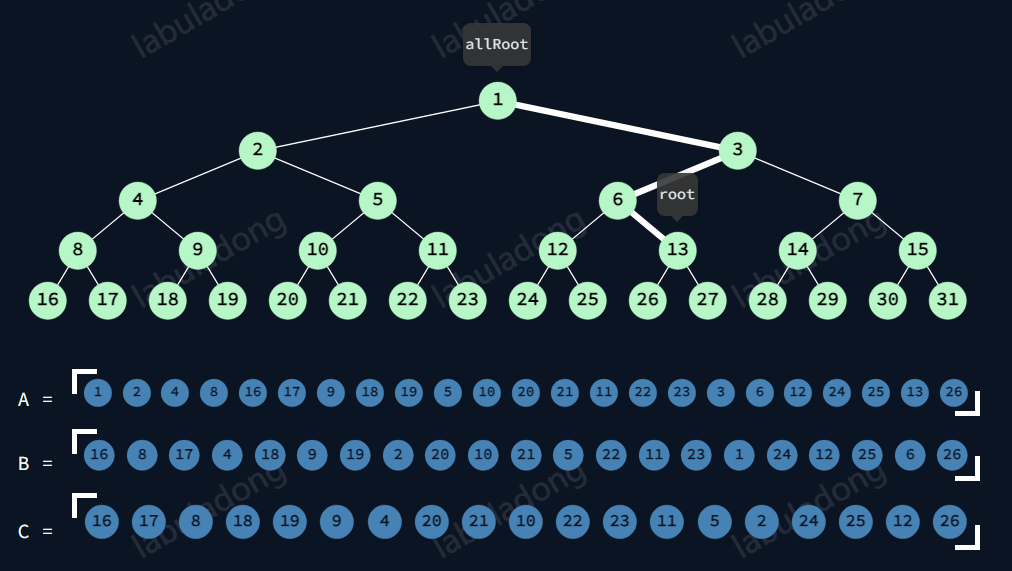
13-Cpush前/后序前

此时
前序结果:
整个13的前序，6+6左树的前序，3，1+1左树的前序。路径节点必有。
中序结果:
整个13的中序，6+6左树的中序，无3，1+1左树的中序。具体判断。
后序结果:
13左树的后序+13右树的后序，12的后序，2的后序。路径的节点必无。

两序重叠

示例一

void traveres(TreeNode* root){

        if(!root)
            return;
        
        A.push_back(root->val);
        
        traveres(root->left);
        
        A.pop_back(root->val);
        
        traveres(root->right);
    }

节点会在中序的时候清空A
那么traveres(root->left);也就是节点左树在中序的时候清空A

13前序前

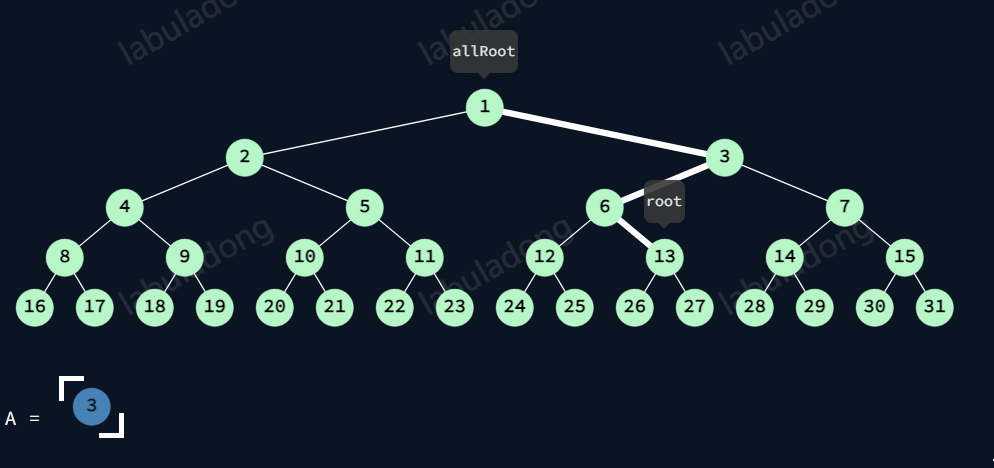
依旧看节点与跟节点的路径。
此时
6遍历完左树。
3没有遍历完左树。
1遍历完左树。
则6清空，有3，1清空。
故A仅剩3。

13中序前

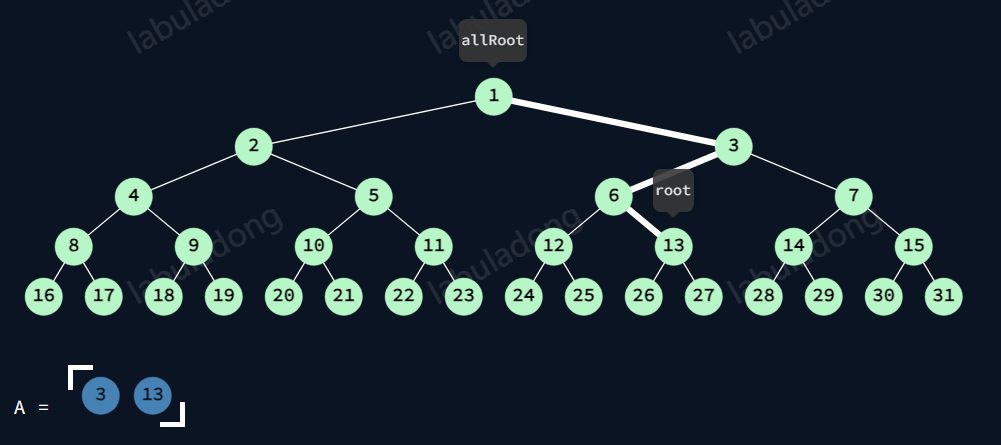
此时，遍历完节点左树，清空。
接着看节点与跟节点的路径。
此时，依旧
6清空，有3，1清空。
故A有3，13。

示例二

    vector<int> A;
    void traveres(TreeNode* root){

        if(!root)
            return;
        
        A.push_back(root->val);
        
        traveres(root->left);
        traveres(root->right);

        A.pop_back(root->val);
    }

节点在后序的时候清空A
那么traveres(root->left);也就是左树在后序的时候清空A。
同理，右树也在后序的时候清空A。

13前序前

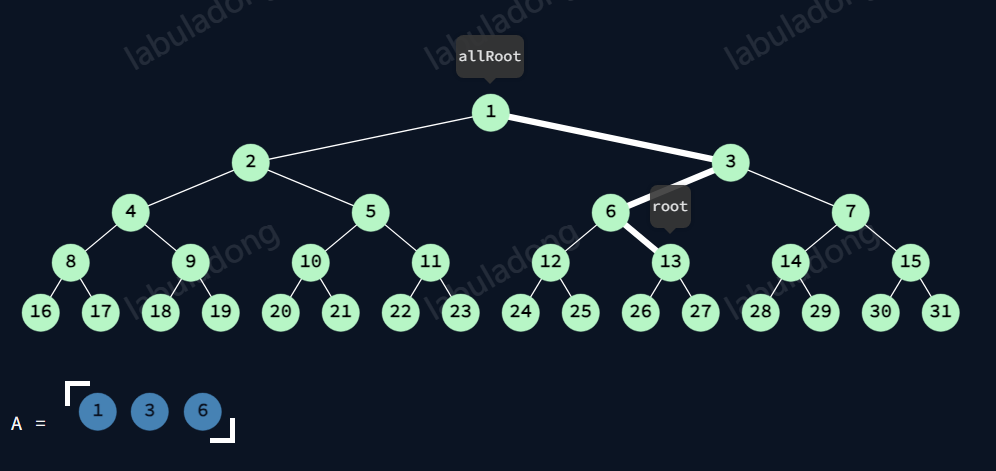
此时，节点与跟节点的路径
6：6的左树遍历完，故左树清空。但右树没有遍历完，故有6。
3：3的左树没有遍历完。故有3。
1：1的左树遍历完，右树没有遍历完，故有1。
故A有1，3，6。

13后序前

此时，节点与跟节点的路径
13：13的左树与右树遍历完。
6：6的左树遍历完。
3：3的左树没有遍历完。
1：1的左树遍历完。
故A有1，3，6，13。

示例三

    vector<int> A;
    
    void traveres(TreeNode* root){

        if(!root)
            return;
        
        traveres(root->left);

        A.push_back(root->val);
        
        traveres(root->right);

        A.pop_back(root->val);
    }

节点在中序的时候入A，在后序的时候清空A。
那么traveres(root->left);左树在中序的时候入A，后序的时候清空A。
同理，右树也在中序的时候入A，后序的时候清空A。

13中序前

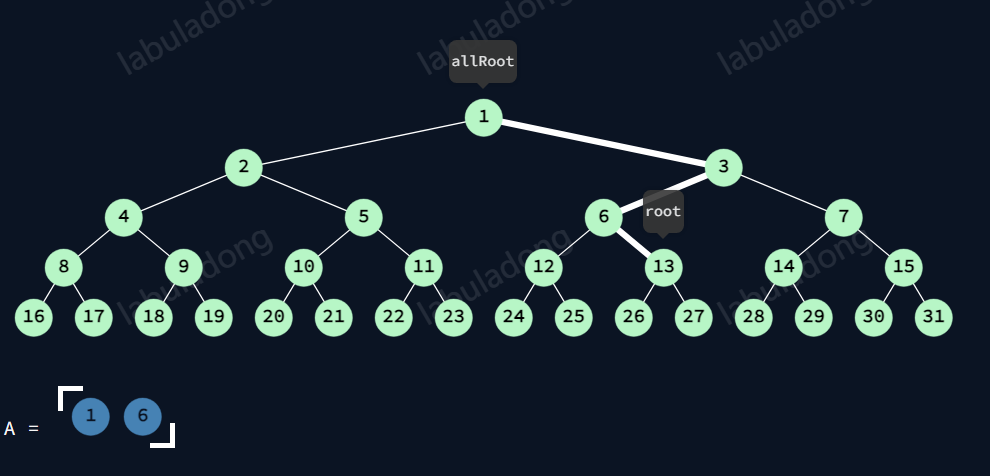
此时，节点与跟节点的路径
13：遍历完左树。还没push。
6：遍历完左树。故有6
3：正在遍历左树。故无3
1：遍历完左树。故有1
故A有1，6。

13后序前

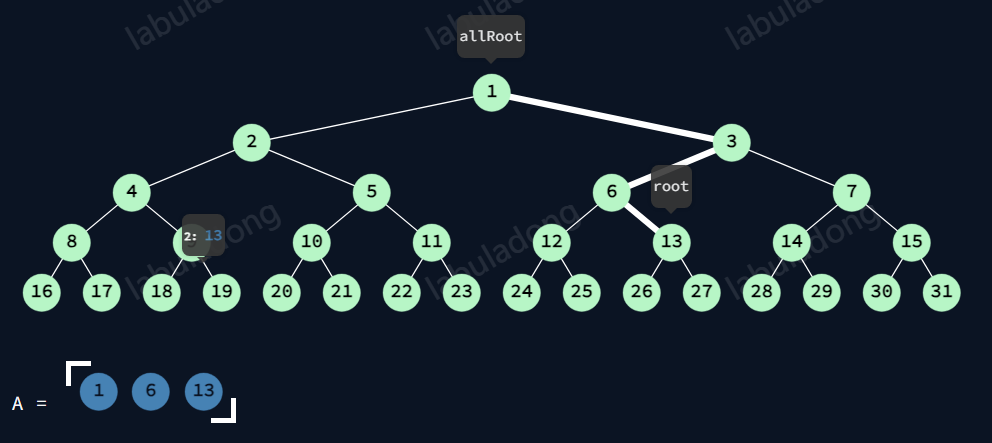
此时，节点与跟节点的路径
13：13的左树与右树遍历完。还没pop。
6：6的左树遍历完。右树没有。
3：3的左树没有遍历完。
1：1的左树遍历完。右树没有
故A有1，6，13。
let allRoot = TreeNode.create([1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,
21,22,23,24,25,26,27,28,29,30,31]);