巴什博弈(Bash Game)

String bashGame2(int n, int m) {
		return n % (m + 1) != 0 ? "先手" : "后手";
	}

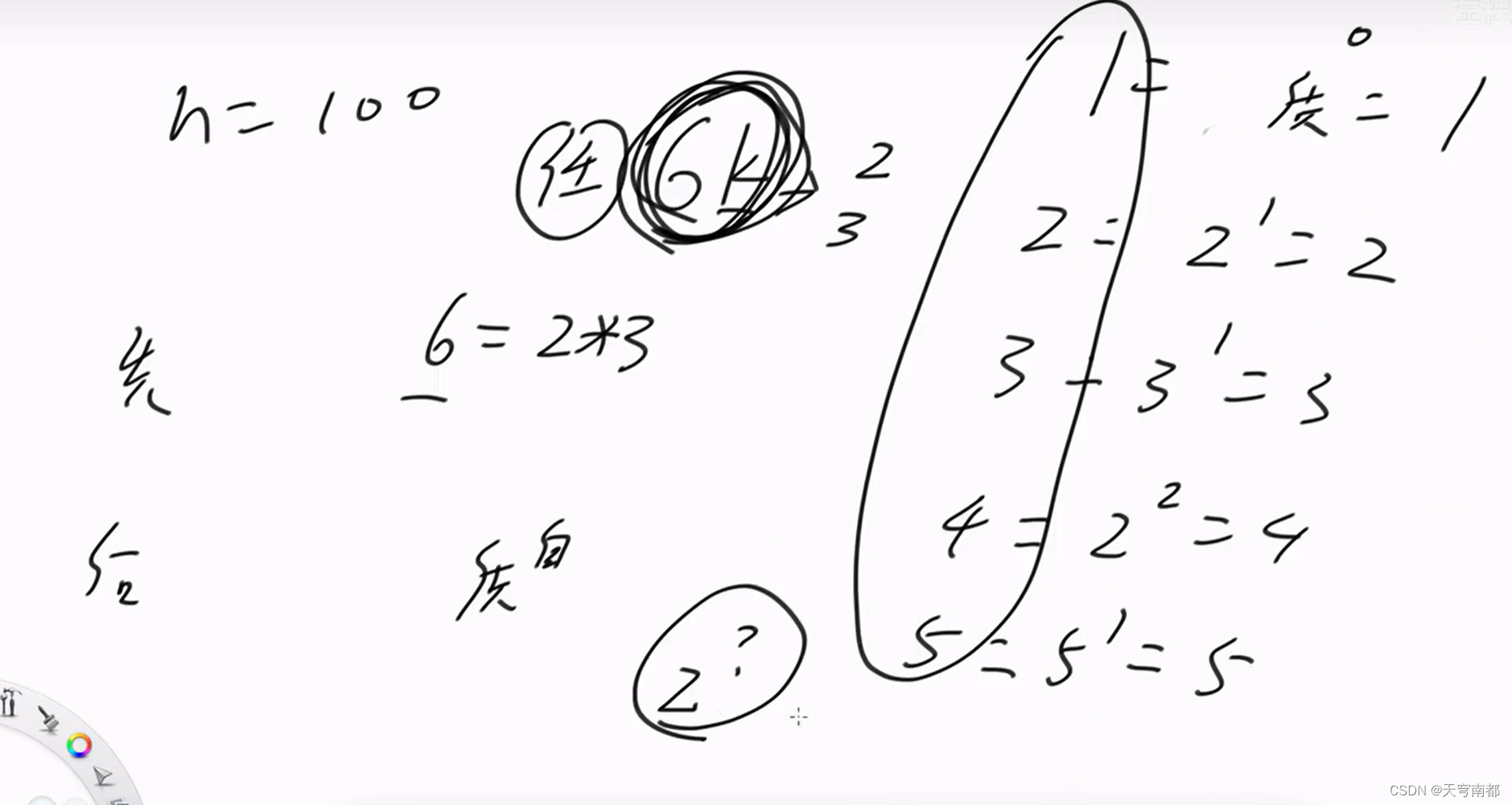
#include<iostream>
#include<string>
using namespace std;

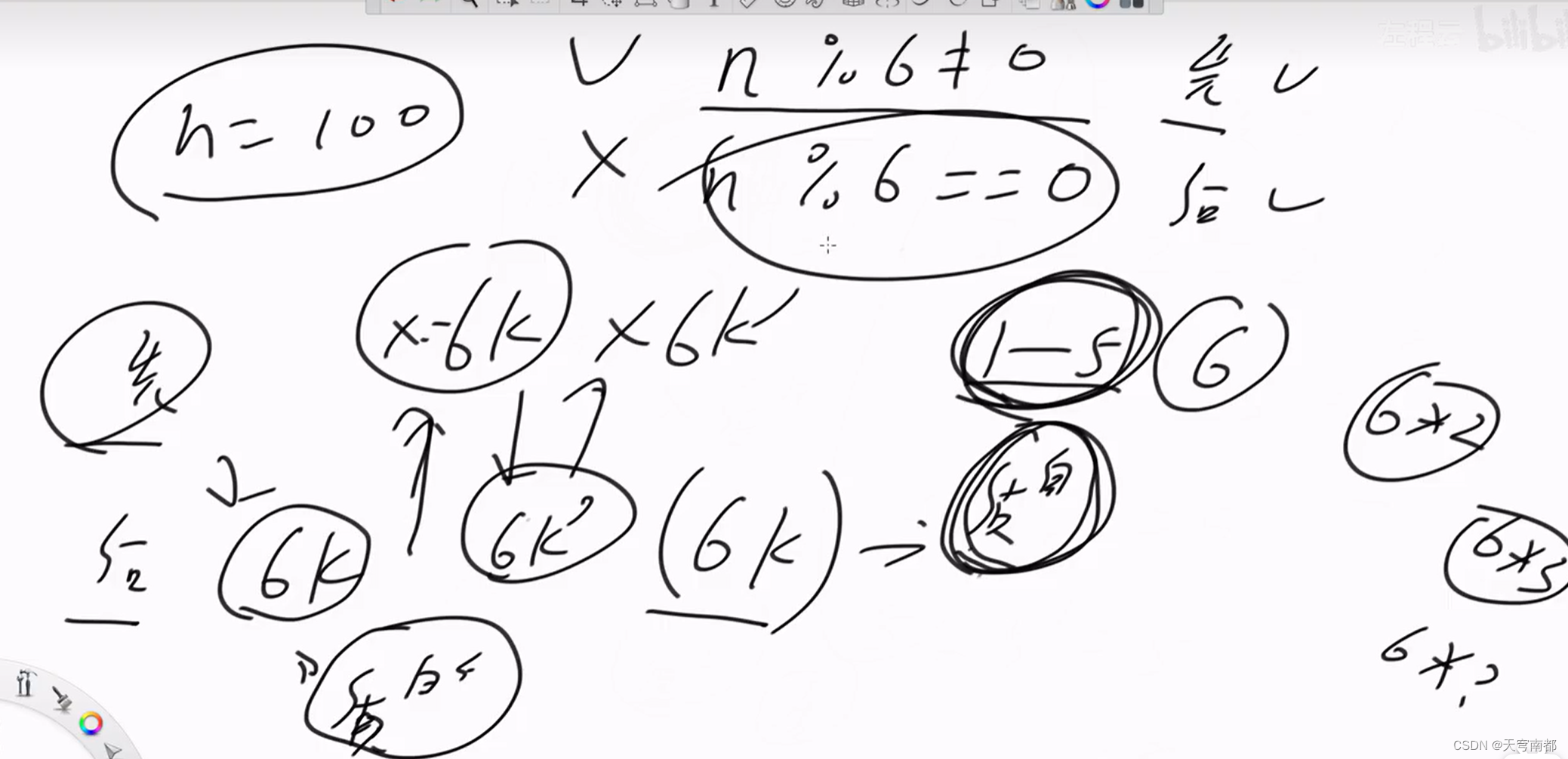
string compute(int n) {
	return n % 6 != 0 ? "October wins!" : "Roy wins!";
}

int main() {
	int t;
	cin >> t;
	for (int i = 0; i < t; i++) {
		int n;
		cin >> n;
		cout << compute(n) << '\n';
	}


	return 0;
}

Nim博弈

异或和等于0减去一个数一定可以变成不等于0

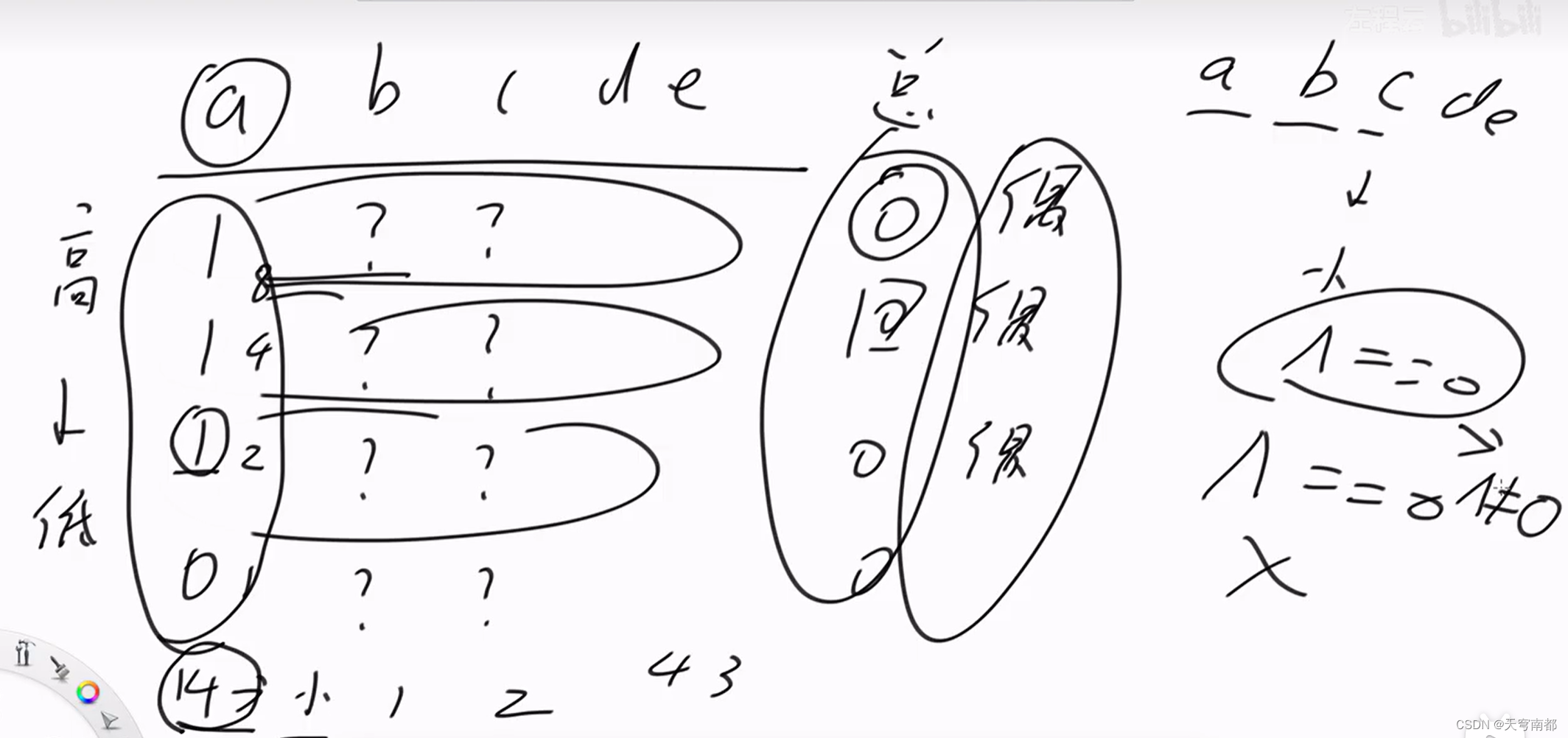
证明： 异或和不等于0减去一个数一定可以变成等于0

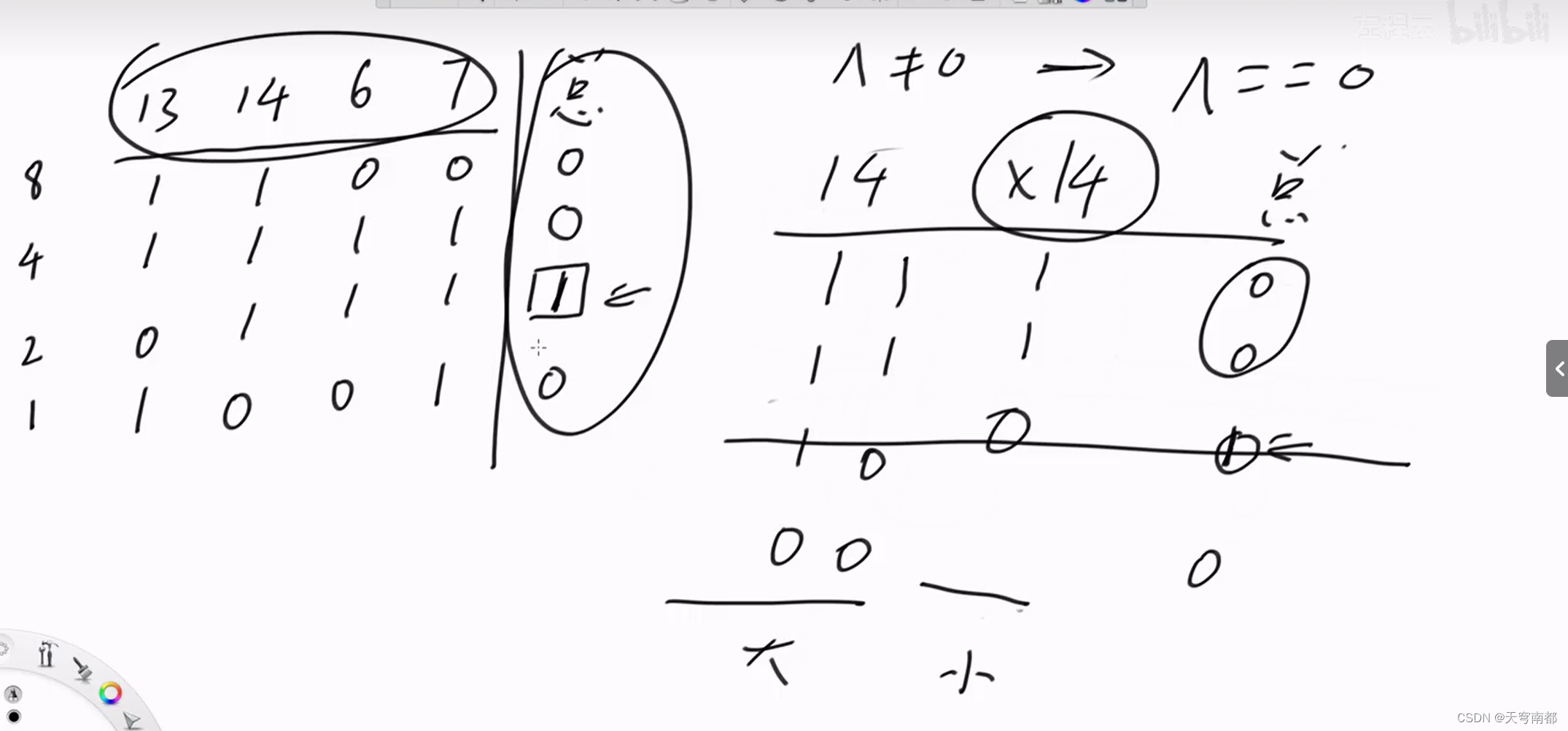
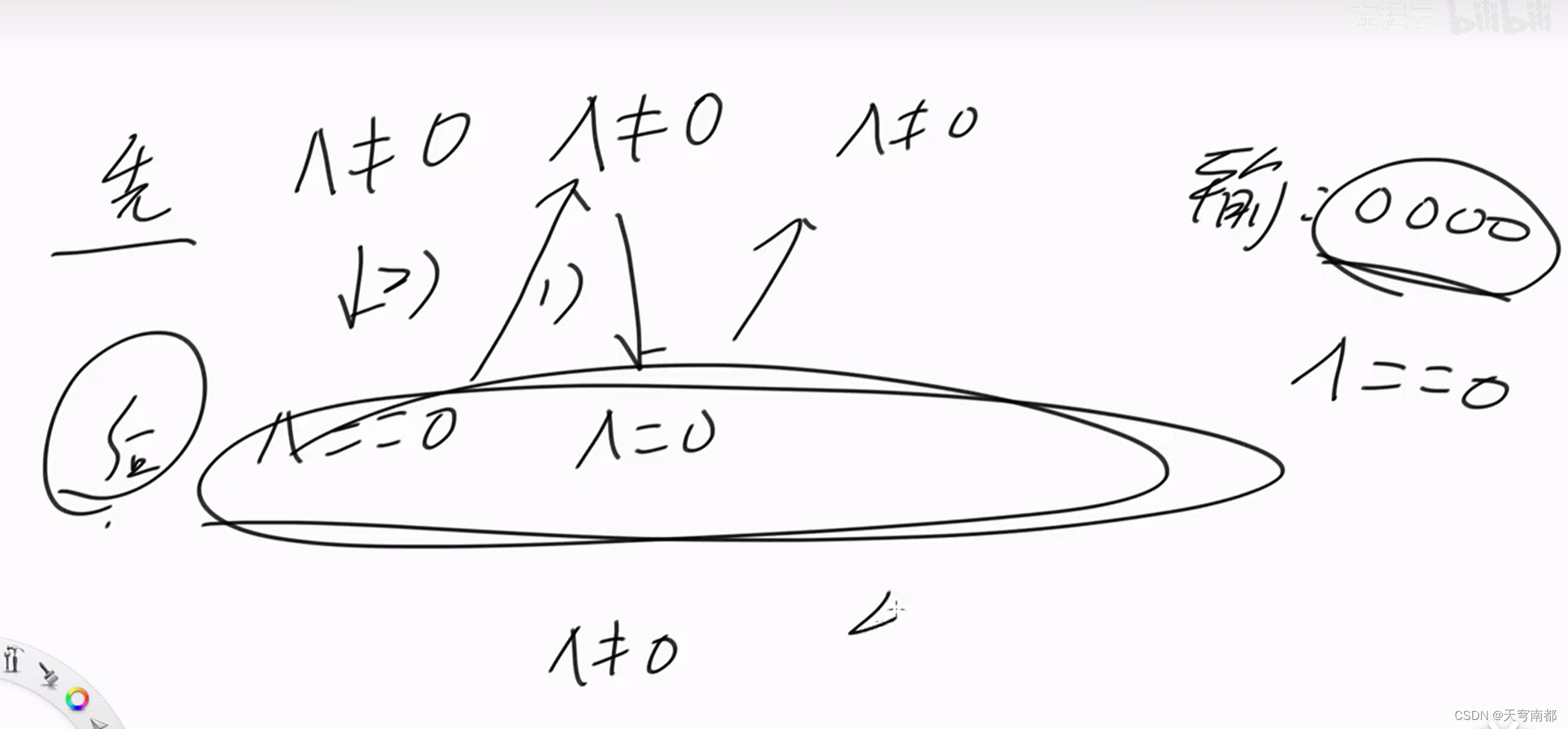
#include<iostream>
#include<string>
using namespace std;

int main() {
	int t;
	cin >> t;
	for (int i = 0; i < t; i++) {
		int n;
		cin >> n;
		int eor = 0;
		for (int j = 0; j < n; j++) {
			int num;
			cin >> num;
			eor ^= num;
		}
		if (eor != 0) {
			cout << "Yes" << '\n';
		}
		else {
			cout << "No" << '\n';
		}
	}
	return 0;
}

反常游戏

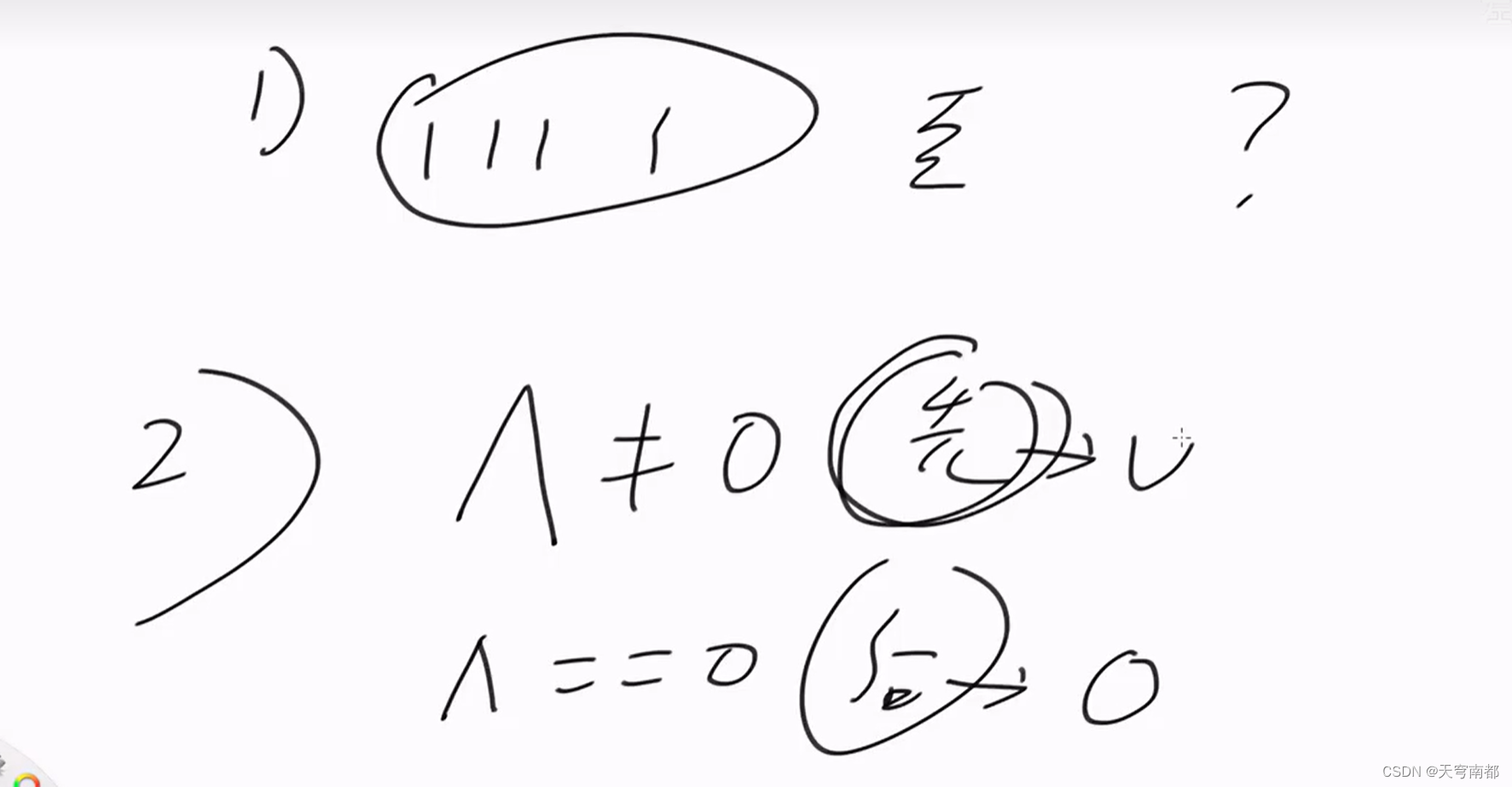
#include<iostream>
#include<string>
using namespace std;

int main() {
	int t;
	cin >> t;
	for (int i = 0; i < t; i++) {
		int n, sum = 0, eor = 0;
		cin >> n;
		for (int j = 0; j < n; j++) {
			int num;
			cin >> num;
			sum += (num == 1) ? 1 : 0;
			eor ^= num;
		}
		if (sum == n) {
			cout << ((n & 1) ? "Brother" : "John")<<'\n';
		}
		else {
			cout << ((eor != 0) ? "John" : "Brother") << '\n';
		}
	}
	return 0;
}

斐波那契博弈

如果石头堆成斐波那契数列

如果不成

齐肯多夫定理（Zeckendorf's theorem）是一个有关斐波那契数列的数学定理。

定理陈述：每一个正整数都可以唯一地表示为若干个不连续的斐波那契数之和。

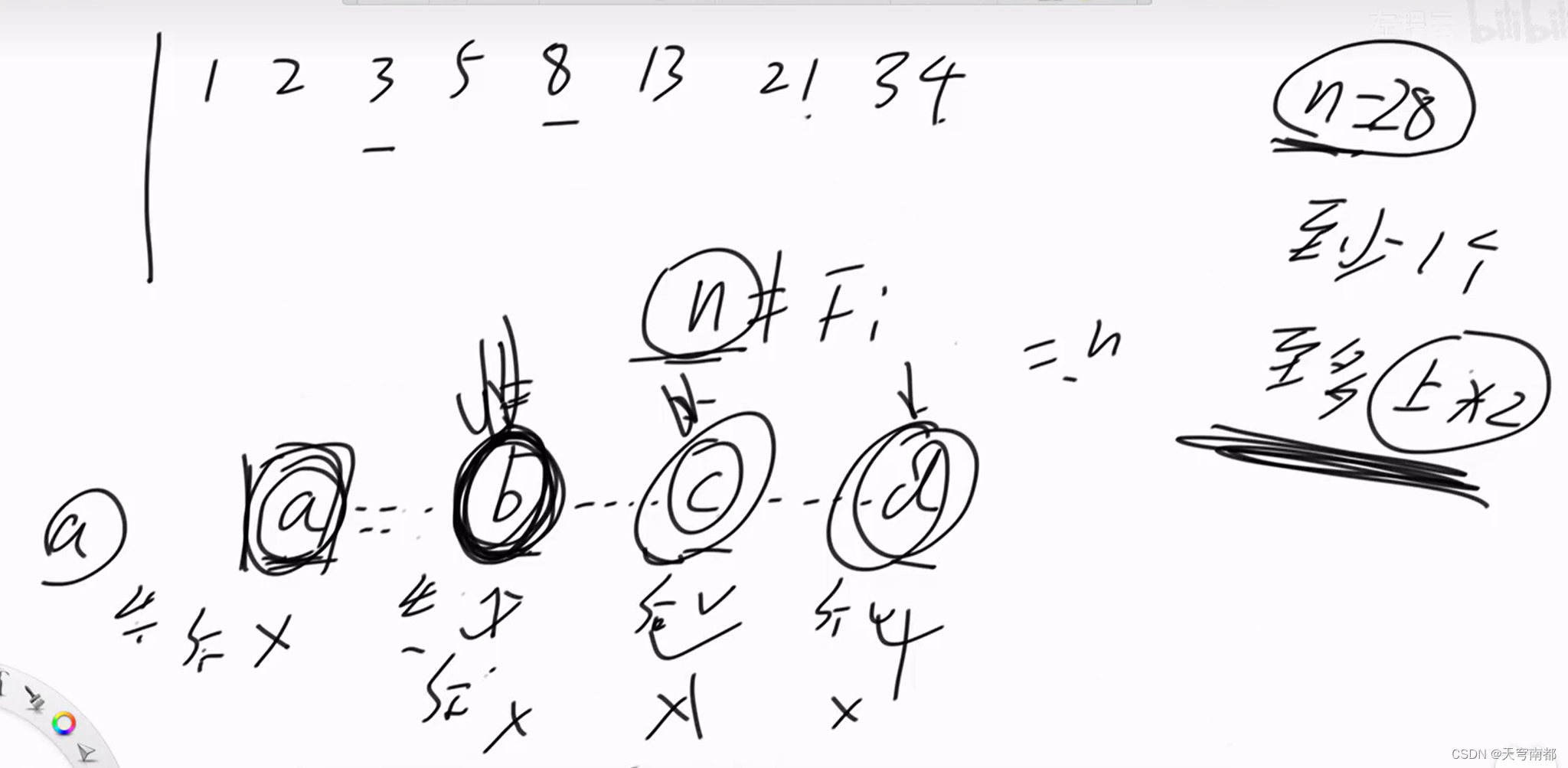
#include<iostream>

typedef long long LL;
const LL N = 1e15;
constexpr int M = 101;
LL f[M];
int size;
void build() {
	f[0] = 1;
	f[1] = 2;
	size = 1;
	while (f[size] <= N) {
		f[size + 1] = f[size] + f[size - 1];
		size++;
	}
}

LL bs(LL n) {
	int l = 0;
	int r = size;
	int m;
	LL ans = -1;
	while (l <= r) {
		m = (l + r) / 2;
		if (f[m] <= n) {
			ans = f[m];
			l = m + 1;
		}
		else {
			r = m - 1;
		}
	}
	return ans;
}

int main() {
	using namespace std;
	build();
	LL n;
	cin >> n;
	LL ans = -1, find;
	while (n != 1 && n != 2) {
		find = bs(n);
		if (n == find) {
			ans = find;
			break;
		}
		else {
			n -= find;
		}
	}
	if (ans != -1)
		cout << ans << '\n';
	else
		cout << n << '\n';

	return 0;
}

  威佐夫博弈