回溯算法理论
回溯是一种效率并不高的穷举算法,因为用暴力算法都解决不了一些问题,所以才会考虑这个方法,它可以解决一系列问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
所有的回溯问题都可以抽象为树形结构,集合的大小构成了树的宽度,递归的深度构成了树的深度。回溯法有以下模板
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
77 组合
给定两个整数 n 和 k,返回 1 ... n 中所有可能的 k 个数的组合。
示例: 输入: n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]
没学习回溯之前,可能会想到for循环的思路,但是如果for循环层数不可控怎么办呢?
回溯法就可以用于解决多层嵌套循环的问题了,组合问题可以抽象为以下树形结构: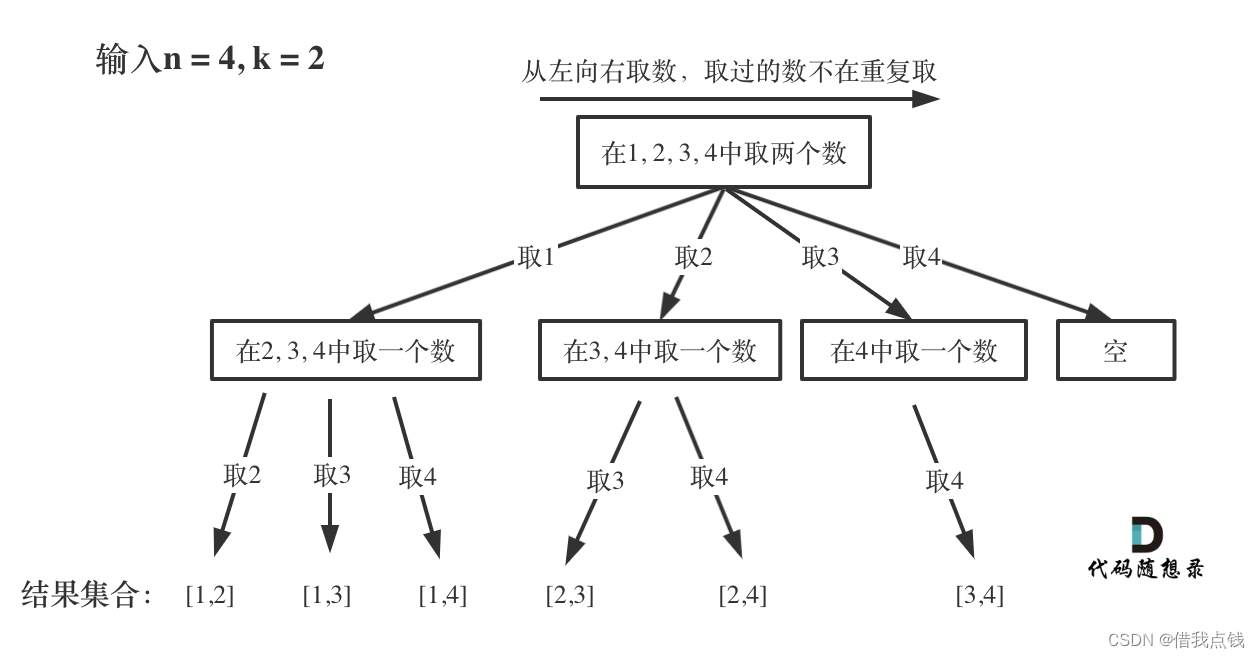
只需要把叶子节点收集起来,就可以求得组合集合了,代码如下:
class Solution {
private:
vector<vector<int>> result; //存放提交的结果
vector<int> path; //存放每一个组合(其实相当于树的路径)
void backtracking(int n, int k, int index) {
if (path.size() == k) {
result.push_back(path); //达到组合大小的时候就可以返回了
return;
}
//从index元素开始,一直遍历到n(后面会写如何剪枝)
for (int i = index; i <= n; i++) {
path.push_back(i); //加入元素
backtracking(n, k, i + 1); // 递归
path.pop_back(); //回溯
}
}
public:
vector<vector<int>> combine(int n, int k) {
result.clear();
path.clear(); //这两行可写可不写
backtracking(n, k, 1);
return result;
}
}; 此题还可以进行一下剪枝操作:原因就是如果从一个index开始,后面的数加起来都不会达到所要求组合的大小,这部分就可以被优化掉了。
可以剪枝的地方就在递归中每一层for循环所选择的起始位置,如果for循环选择的起始位置之后的元素个数已经不足我们需要的元素个数了,那么就没有必要搜索了。
已经选择的元素个数为path.size(),还需要组成组合的元素为k-path.size(),在集合n中之多要从起始位置n-(k-path.size())+ 1开始遍历,超过了这个数的话,后面就不够凑齐组合了,优化以后的for循环为:
for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置216 组合总和
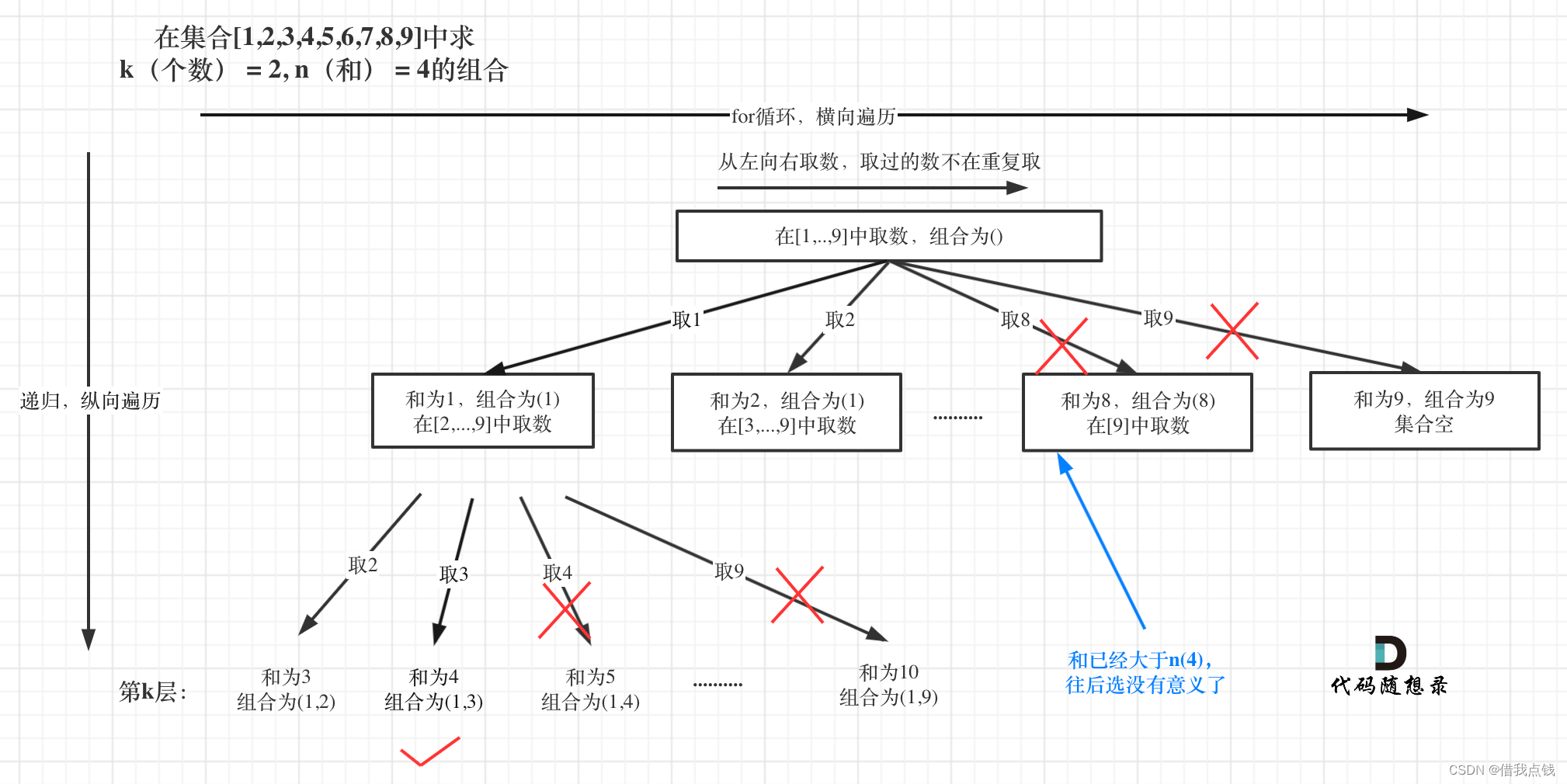
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
本题与上一题类似,只是多了一个求和条件,这里加了剪枝操作。
class Solution {
private:
vector<vector<int>> result; // 存放结果集
vector<int> path; // 符合条件的结果
void backtracking(int targetSum, int k, int sum, int startIndex) {
if (sum > targetSum) { // 剪枝操作
return;
}
if (path.size() == k) {
if (sum == targetSum) result.push_back(path);
return; // 如果path.size() == k 但sum != targetSum 直接返回
}
for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) { // 剪枝
sum += i; // 处理
path.push_back(i); // 处理
backtracking(targetSum, k, sum, i + 1); // 注意i+1调整startIndex
sum -= i; // 回溯
path.pop_back(); // 回溯
}
}
public:
vector<vector<int>> combinationSum3(int k, int n) {
result.clear(); // 可以不加
path.clear(); // 可以不加
backtracking(n, k, 0, 1);
return result;
}
};
记得二叉树里面有一题直接用了减法,也可以用减法来看就不需要sum了:
class Solution {
private:
vector<vector<int>> result; // 存放结果集
vector<int> path; // 符合条件的结果
void backtracking(int targetSum, int k,int startIndex) {
if (targetSum < 0) { // 剪枝操作
return;
}
if (path.size() == k) {
if (targetSum == 0) result.push_back(path);
return;
}
for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) { // 剪枝
targetSum -= i; // 处理
path.push_back(i); // 处理
backtracking(targetSum, k, i + 1); // 注意i+1调整startIndex
targetSum += i; // 回溯
path.pop_back(); // 回溯
}
}
public:
vector<vector<int>> combinationSum3(int k, int n) {
result.clear(); // 可以不加
path.clear(); // 可以不加
backtracking(n, k, 1);
return result;
}
};