1, 算法原理

设th 是一个弧度值，
令

Q = | cos(th)  sin(th) |
       | sin(th) -cos(th) |
    
S = span{ | cos(th/2.0) | }
                 | sin(th/2.0)  |
        
x = (x1, x2) 是一个平面上的二维向量

计算
y = Q'x = Qx

则，y 是 x 通过有 S 定义的直线作为镜面，反射而达到的像。

2. 代码

draw_householder.m

%input x, ta = theta

%x = [-sqrt(2)/2.0, sqrt(2)/2.0]
x = [-1.2, 1.2]
ta = 2.0

S = [cos(ta/2.0), sin(ta/2.0)]
Q = [cos(ta), sin(ta); sin(ta), -cos(ta);]

y = x*Q'


figure;
%1. draw axis
xmin = -2
xmax = 2
ymin = -2
ymax = 2

axisx = xmin:xmax;
axisy = zeros(size(axisx));
plot(axisx, axisy, 'k--', 'LineWidth', 0.7); % Plot x=0 axis
hold on;
plot(axisy, xmin:xmax, 'k--', 'LineWidth', 0.7); % Plot y=0 axis
hold on;

%2. draw surface of mirror
sx = -2*S(1):0.1:2*S(1)
sy = (S(2)/S(1))*sx
plot(sx, sy)
hold on;

%3. draw preimage
plot(x(1), x(2), 'ro')
hold on;

%4. draw image
plot(y(1), y(2), 'bo')

%5. axis label
xlabel("X")
ylabel('Y')
v=[xmin, xmax, ymin, ymax]
axis(v)
%axis on

3, 效果图

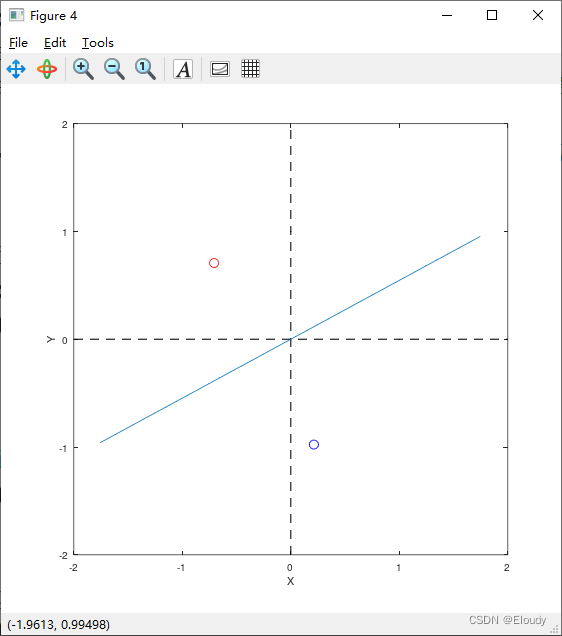
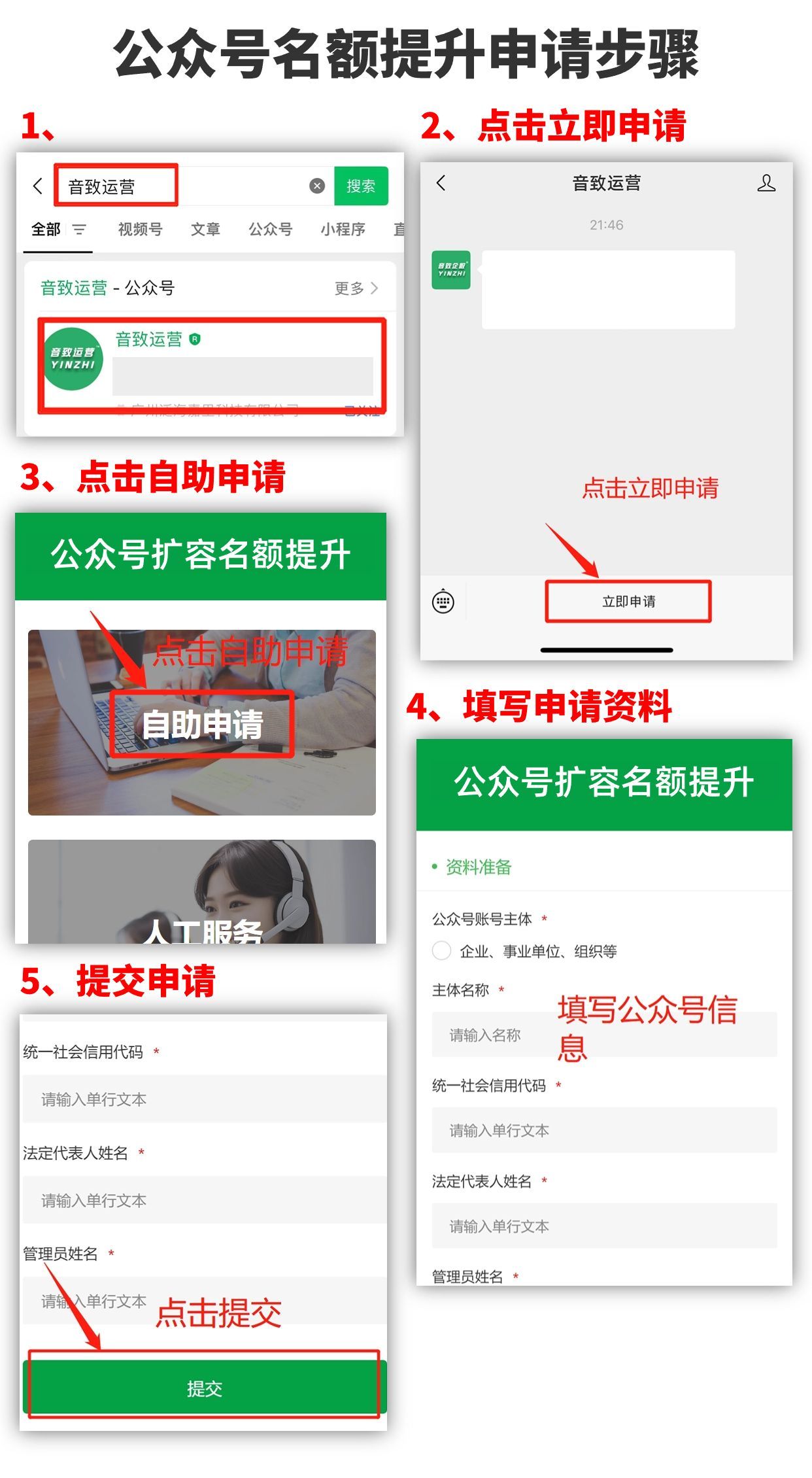
下面这张图为

x=(-1.2, 1.2), theta = 2.0 弧度

下图为

x=(0.7, 0.3), theta = 1.0 弧度

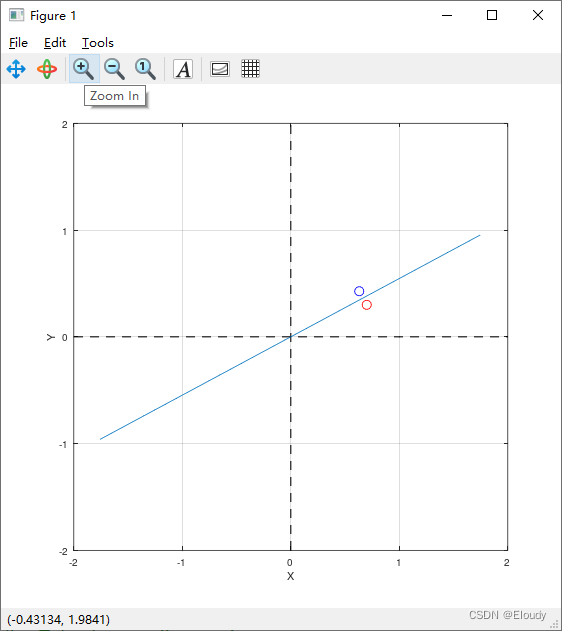
下图为

x = [-sqrt(2)/2.0, sqrt(2)/2.0]   ， theta = 1.0弧度