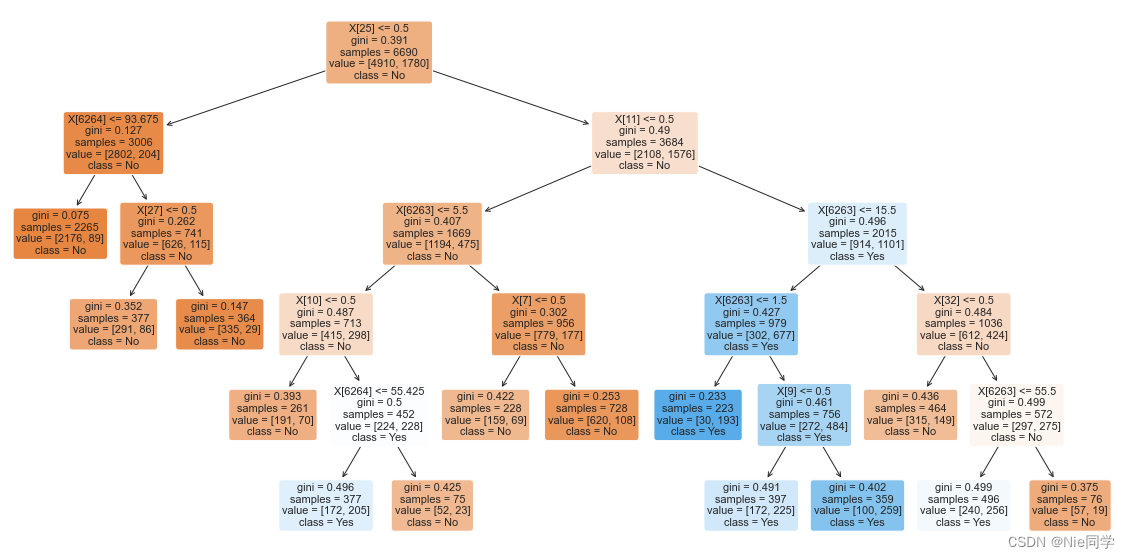
二叉树的重构

集合实现对图的dfs,bfs复写

插入排序

霍夫曼树，霍夫曼编码

查找成功，查找失败的期望值计算

9.给定散列表大小为11，散列函数为H(Key)=Key%11。按照线性探测冲突解决策略连续插入散列值相同的4个元素。问：此时该散列表的平均不成功查找次数是多少？
A.1
B.4/11
C.21/11
D.不确定

答案：C

分析：
区别概念平均成功查找次数和平均不成功查找次数。
平均成功查找次数=每个关键词比较次数之和÷关键词的个数
平均不成功查找次数=每个位置不成功时的比较次数之和÷表长（所谓每个位置不成功时的比较次数就是在除余位置内，每个位置到第一个为空的比较次数，比如此题表长为11，散列函数为Key%11，除余的是11，那么除余位置就是0—10；如果表长为15，但散列函数为Key%13，那么除余位置就是0—12）
明确概念后做题：
连续插入散列值相同的4个元素，我们就假设它的散列值都为0，那么插入后的位置：

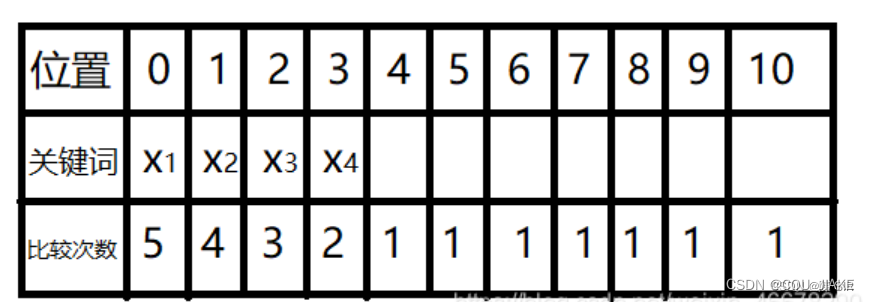
其中位置0到第一个为空的位置4的比较次数为5，其余的位置以此类推。
平均不成功查找次数=（5+4+3+2+1+1+1+1+1+1+1）÷ 11 = 21/11
故选C

线性探测法

#include <bits/stdc++.h>
#define LL long long
using namespace std;
 
const int N=10100;
int n, m , idx;
int p[N];
bool st[N],fg=true;
 
 
int main() {
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        cin >> idx;
        int x = idx % m;
        while (st[x] && p[x] != idx) { x++; if (x == m)x = 0; }
        st[x] = true;
        p[x] = idx;
        if (fg) {
            fg = false;
            cout << x;
        }
        else cout << " " << x;
    }
    return 0;
}

#include <bits/stdc++.h>
#define LL long long
using namespace std;
 
const int N=10100;
int n, m ;

 
 
int main() {
    cin >> n >> m;
    int p[N];
bool st[N],fg=true;
    for (int i = 1; i <= n; i++) {
        int num;
        cin >> num;
        int index = num % m;
        while (st[index] && p[index] != num) { index++; if (index == m)index = 0; }
        st[index] = true;
        p[index] = num;
        if (fg) {
            fg = false;
            cout << index;
        }
        else cout << " " << index;
    }
    return 0;
}

这是一个使用线性探测法解决冲突的哈希表实现的代码。代码中的主要逻辑如下：

1. 从输入中读取n和m，分别表示输入元素的数量和哈希表的大小。

2. 创建一个数组p和一个布尔数组st，分别用来存储哈希表的元素和表示每个位置是否被占用的状态。

3. 循环n次，读取每个元素的值，并计算其哈希值x。

4. 如果哈希表位置x已经被占用且不等于当前元素的值，使用线性探测法找到下一个可用位置，即向后遍历哈希表，直到找到一个未被占用的位置。

5. 标记位置x为已占用，将当前元素的值存储在位置x上。

6. 输出当前元素的哈希值x。

7. 循环结束后，输出每个元素对应的哈希值。

这段代码的功能是将n个输入的元素通过哈希函数映射到大小为m的哈希表中，并输出每个元素的哈希值。使用线性探测法可以处理哈希冲突，即当两个元素映射到同一个位置时，通过线性探测法找到下一个可用位置。

#include<iostream>
using namespace std;
int main(){
    int n,p;
    cin>>n>>p;
    int arr[p];
    bool st[p];
    for(int i=1;i<=n;i++){
        int num;
        cin>>num;
        int index=num%p;
        while(st[index]&&arr[index]!=num){
           index=(index+1)%p;
        }
        st[index]=true;
        arr[index]=num;
        cout<<num%p;
        if(i!=n)cout<<" ";
    }
    return 0;
}