✨✨ 欢迎大家来到贝蒂大讲堂✨✨
🎈🎈养成好习惯,先赞后看哦~🎈🎈
所属专栏:C语言学习
贝蒂的主页:Betty‘s blog
引言
我们早就学完基本的数据类型,那这些数据类型到底在内存中怎么存储的呢~,今天贝蒂就带大家一起深入学习一下吧
1. 数据类型
1.1 整型
有符号字符型:(signed) char// 1字节
无符号字符型:unsigned char// 1字节
有符号短整型:(signed) short// 2字节
无符号短整型:unsigned short// 2字节
有符号整型:(signed) int// 4字节
无符号整型:unsigned int// 4字节
有符号长整型:(signed) long// 4字节
无符号长整型:unsigned long// 4字节
有符号更长整型:(signed) long long// 8字节
无符号更长整型:unsigned long long// 8字节
贝蒂说:“因为字符在内存中是以ASCII的形式存储,所以也是整型哦~”
1.2 浮点型
单精度浮点型:float //4字节
双精度浮点型:double //8字节
1.3 构造类型
数组类型
结构体类型:struct
枚举类型:enum
联合类型:union
贝蒂说:“结构体,枚举等类型大小将在后续章节为大家详细讲解哦~”
1.4 指针类型
//32位环境下指针变量大小 4
//64位环境下指针变量大小 8
字符指针:char*
短整型指针:short*
整型指针:int*
长整型指针:long*
更长类型指针:long long*
单精度浮点数指针:float*
双精度浮点数指针:double*
空类型指针:void*
1.5 空类型
void
//void代表无类型,常用在程序编写中对定义函数的参数类型、返回值、函数中指针类型进行声明。
2. 整型的存储
我们知道计算机存储数据是以二进制的方式,那具体是以怎样的方式存储呢~
整数的二进制表⽰⽅法有三种,即原码、反码和补码。
对于有符号整数,三种表⽰⽅法均有符号位和数值位两部分,符号位都是⽤0表⽰“正”,⽤1表⽰“负”,⽽数值位最⾼位的⼀位是被当做符号位,剩余的都是数值位;对于**无符号整数,**全是数值位。
一个整型(int)4个字节,一个字节八个比特位,所以整型有32位二进制序列。
其中正数的原码,反码,补码相同。
负数如下:
(1)原码
//直接将负数翻译成二进制就可以。
//以-1为例
//原码:100000000000000000000000000000000001
(2)反码
//对原码除符号位之外的每一位按位取反
//以-1为例
//反码:11111111111111111111111111111110c
(3)补码
//反码加1
//以-1为例
//补码:11111111111111111111111111111111
而整型在内存中是以补码的形式存储的,这是为什么呢?我们以一个例子说明一下
int main()
{
int a = 1;
int b = -1;
//a是正数,原码,反码,补码相同
//00000000000000000000000000000001
//b是负数,原码,反码,补码需要相互转化
//10000000000000000000000000000001--原码
//11111111111111111111111111111110--反码
//11111111111111111111111111111111--补码
//假设正数负数都使用原码
//00000000000000000000000000000001 --a的原码
//10000000000000000000000000000001 --b的原码
//10000000000000000000000000000010 --和为-2(错误)
//
//11111111111111111111111111111111 --b的补码
//00000000000000000000000000000001 --a的原码
//00000000000000000000000000000000 --和为0(正确)
return 0;
}
当然补码的好处不止这些,此外,补码与原码相互转换,其运算过程是相同的,不需要额外的硬件电路。
3. 大小端
3.1 什么是大小端
其实超过⼀个字节的数据在内存中存储的时候,就有存储顺序的问题,按照不同的存储顺序,我们分为⼤端字节序存储和⼩端字节序存储,下⾯是具体的概念:
⼤端(存储)模式:是指数据的低位字节内容保存在内存的⾼地址处,⽽数据的⾼位字节内容,保存在内存的低地址处。
⼩端(存储)模式:是指数据的低位字节内容保存在内存的低地址处,⽽数据的⾼位字节内容,保存在内存的⾼地址处。
具体是什么意思呢~
首先我们得知道内存中数据是以16进制表示的
int a=0x11223344//十六进制表示
那么它就可能有两种表示形式

3.2 如何判断大小端
方法一:
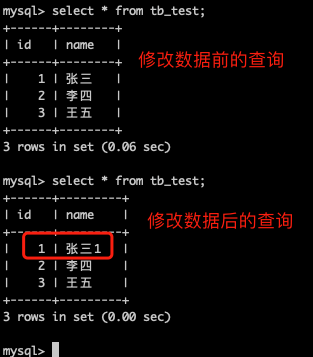
直接通过调用内存观察
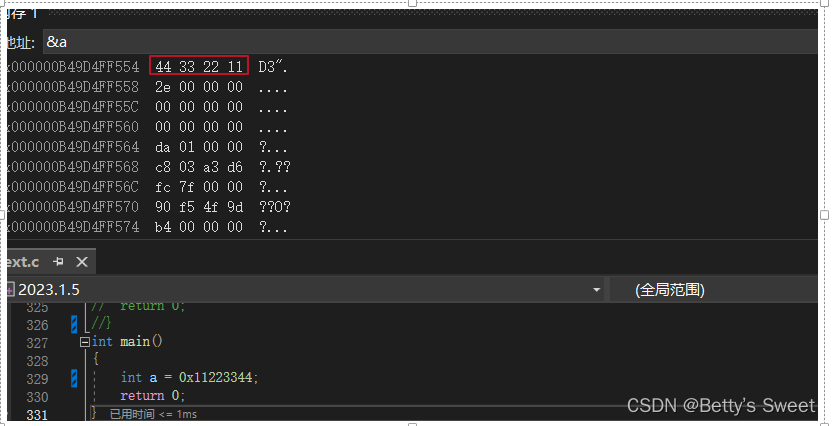
通过上述图像,我们知道在vs的环境下,数据是小端存储的~
方法二:
我们可以通过代码判断
那我们该如何通过代码判断呢~

那我们如何取出第一位呢~,这就需要我们对指针的灵活运用了
我们知道第一位相当于一个字节,而char类型就是一个字节,所以以(*char)取出就行了
代码如下:
#include <stdio.h>
int check_sys()
{
int i = 1;
return (*(char*)&i);//取出第一位
}
int main()
{
int ret = check_sys();
if (ret == 1)
{
printf("⼩端\n");
}
else
{
printf("⼤端\n");
}
return 0;
}
4. 整型截断
4.1 理解
整型截断是将所占字节大的元素赋给所占字节小的元素时会出现数值的舍去现象。
简单来说就是将长字节内容截取一部分赋给短字节内容
4.2 举例
char i = -1;//-1是整型4个字节,char类型1个字节,发生整型截断

5. 整型提升
5.1 理解
C的整型算术运算总是至少以缺省(默认)整型类型的精度来进行的。为了获得这个精度,表达式中的字符和短整型操作数在使用之前被转换为普通整型,这种转换称为整型提升。
有符号的整型提升高位补符号位,无符号的整型提升高位补0。
5.2 举例
(1) 正数的整型提升
char a=1;
//补码:00000001
//有符号,符号位是0,提升为00000000000000000000000000000001
(2) 负数的整形提升
char b=-1;
//补码:1111111
//有符号,符号位是1,提升为11111111111111111111111111111111
(3) 无符号数的整型提升
unsigned c=-1
//补码:1111111
//无符号,补0,提升为00000000000000000000000011111111
6. 算数转换
6.1 理解
如果某个操作符的各个操作数属于不同的类型,那么除⾮其中⼀个操作数的转换为另⼀个操作数的类型,否则操作就⽆法进⾏。下⾯的层次体系称为寻常算术转换。
long double
double
float
unsigned long int
long int
unsigned int
int
如果某个操作数的类型在上⾯这个列表中排名靠后,那么⾸先要转换为另外⼀个操作数的类型后执⾏运算。
6.2 举例
#include<stdio.h>
int main()
{
int a=3;
float b=1.5;
float c =a+b;
//算术转换,int-->float
return 0;
}
7. 练习题
7.1 练习一
#include <stdio.h>
//会输出什么
int main()
{
char a = -1;
//-1的原码:10000000000000000000000000000001
//-1的反码:11111111111111111111111111111110
//-1的补码:11111111111111111111111111111111
signed char b = -1;
unsigned char c = -1;
//a、b、c均存储为11111111
printf("a=%d,b=%d,c=%d", a, b, c);
//以%d输出发生整型提升
//有符号的a、b整型提升为11111111111111111111111111111111——>-1
//无符号的c整型提升为00000000000000000000000011111111——>255
return 0;
}
输出结果:
a=-1,b=-1,c=255
7.2 练习二
#include <stdio.h>
//输出什么
int main()
{
char a = -128;
//原码:10000000000000000000000010000000
//反码:11111111111111111111111101111111
//补码:11111111111111111111111110000000
//发生整型截断a为10000000
printf("%u\n", a);
//发生整型提升,a有符号,补符号位,11111111111111111111111110000000
//以无符号整型输出,4294967168
return 0;
}
输出:4294967168
7.3 练习三
#include <stdio.h>
//输出什么
int main()
{
int i = -20;
//原码:10000000000000000000000000010100
//反码:11111111111111111111111111101011
//补码:11111111111111111111111111101100
unsigned int j = 10;
//原,反,补相同:00000000000000000000000000001010
printf("%d\n", i + j);
// 11111111111111111111111111101100 + 00000000000000000000000000001010
// =11111111111111111111111111110110——>有符号输出-10
return 0;
}
-10
7.4 练习四
int main()
{
//输出什么?
unsigned int i;
for (i = 9; i >= 0; i--)
{
printf("%u ", i);
}
//先判断,再--,最后0-1=-1
//-1原码:10000000000000000000000000000001
//-1的反码:11111111111111111111111111111110
//-1的补码:11111111111111111111111111111111——>以无符号打印一个非常大的整数
//以此往复
//最后会发生死循环
return 0;
}
9 8 7 6 5 4 3 2 1 0…死循环
7.5 练习五
int main()
{
//输出什么
char a[1000];
int i;
for (i = 0; i < 1000; i++)
{
a[i] = -1 - i;
//有符号char 最小 11111111 最高位为符号位 ——>-127
//但是C语言又特别规定10000000为——>-128
//最大为 01111111 ——>127
//所以有符号char范围为-128~127
}
printf("%d", strlen(a));//以字符'\0'(ASCII值为0)为结束标志
//-129的原码:10000000000000000000000010000001
//-129的反码:11111111111111111111111101111110
//-129的补码:11111111111111111111111101111111
//发生整型截断:01111111——>127
//所以a[i]的数据为-1,-2,-3.....-128,127,126......1,0
//长度为128+127=255
return 0;
}
输出结果:
255
7.6 练习六
unsigned char i = 0;
int main()
{
for (i = 0; i <= 255; i++)
{
printf("hello world\n");
}
//无符号最小为0,最大为11111111,范围0~255
//而我的i<=255,所以代码会一直循环打印hello world
return 0;
}
8. 浮点数的存储
浮点数的存储规则和整型一样吗?答案自然是不同的,具体哪里不同,咋们接着往下看~
8.1 浮点数的存储规则
根据国际标准IEEE(电⽓和电⼦⼯程协会)?754,任意⼀个⼆进制浮点数V可以表⽰成下⾯的形式:
V = (−1) ^S*M *2 E
• (-1)^S 表⽰符号位,当S=0,V为正数;当S=1,V为负数
• M表⽰有效数字,M是⼤于等于1,⼩于2的
• 表⽰指数位
8.2 举例
⼗进制的5.0,写成⼆进制是 101.0 ,相当于 1.01×2^2 。
那么,按照上⾯V的格式,可以得出S=0,M=1.01,E=2。
⼗进制的-5.0,写成⼆进制是 -101.0 ,相当于 -1.01×2^2 。那么,S=1,M=1.01,E=2。
IEEE 754规定:
对于32位的浮点数,最⾼的1位存储符号位S,接着的8位存储指数E,剩下的23位存储有效数字M

对于64位的浮点数,最⾼的1位存储符号位S,接着的11位存储指数E,剩下的52位存储有效数字M
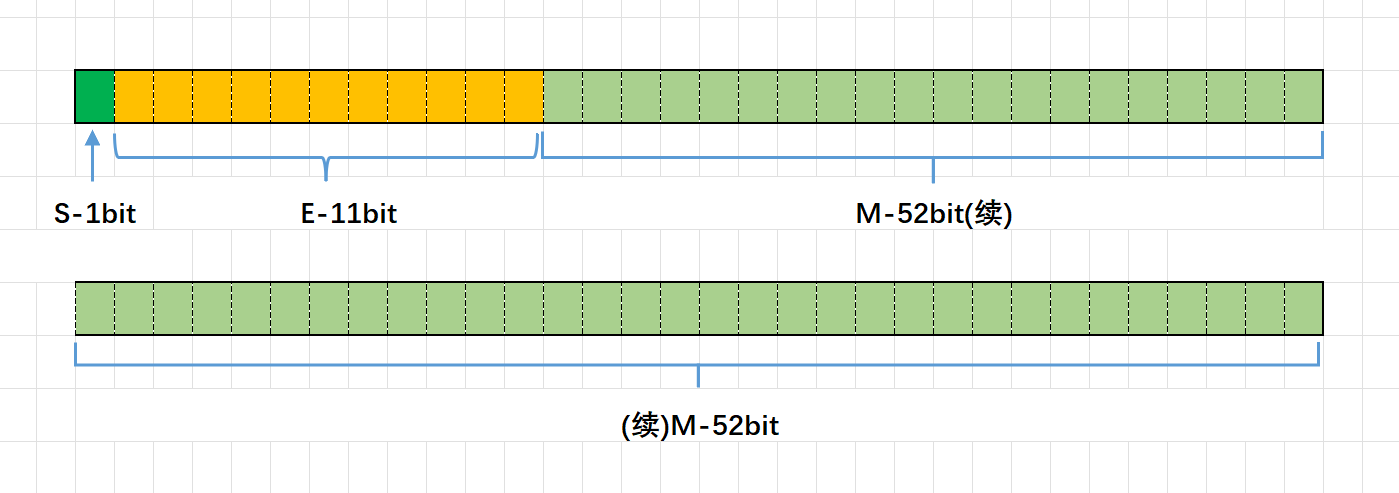
8.3 浮点数取得过程
(1) 对于M的规定
1 ≤ M < 2 ,即M可以写成1.xxxxxx的形式。IEEE 754规定,在计算机内部保存M时,默认这个数的第一位总是1,因此可以被舍去,只保存后面的xxxxxx部分。比如保存1.01的时候,只保存01,等到读取的时候,再把第一位的1加上去。这样做的目的,是节省1位有效数字。以32位浮点数为例,留给M只有23位,将第一位的1舍去以后,等于可以保存24位有效数字。
(2) 对于E的规定
E为一个无符号整数(unsigned int),如果E为8位,它的取值范围为0 ~ 255;如果E为11位,它的取值范围为0 ~ 2047。但是,科学计数法中的E是可以出现负数的,所以IEEE 754规定,存入内存时E的真实值必须再加上一个中间数,对于8位的E,这个中间数127;对于11位的E,这个中间数是1023。 例如,2^10的E是10,所以保存成32位浮点数时,必须保存成10+127=137,即10001001。
指数E从内存中取出还可以再分成三种情况:
1. E不全为0或不全为1
这时,浮点数就采⽤下⾯的规则表⽰,即指数E的计算值减去127(或1023),得到真实值,再将有效数字M前加上第⼀位的1。
如一个浮点数存储方式如下:
0 01111110 00000000000000000000000
-
首先将 01111110 转换为十进制为126
-
再将126-127=-1,所以指数位为-1
-
有效数字部分为0,所以表示1.0
-
符号位0,是个正数,所以表示的浮点数是1.0*2^-1=0.5
2. E全为0
这时候指数为0-127,最后肯定得到一个很小的数,所以特别规定
这时,浮点数的指数E等于1-127(或者1-1023)即为真实值,有效数字M不再加上第⼀位的1,⽽是还原为0.xxxxxx的⼩数。这样做是为了表⽰±0,以及接近于0的很⼩的数字。
3. E全为1
255 - 127 = 128 或 2047 - 1023 = 1024, 与第二点相反,这时这个数可能无强大,所以也特别规定
这时,如果有效数字M全为0,表⽰±⽆穷⼤(正负取决于符号位s)
8.4 列题
#include <stdio.h>
//打印出什么
int main()
{
int n = 9;
float* pFloat = (float*)&n;
printf("n的值为:%d\n", n);
printf("*pFloat的值为:%f\n", *pFloat);
*pFloat = 9.0;
printf("num的值为:%d\n", n);
printf("*pFloat的值为:%f\n", *pFloat);
return 0;
}
- 先将整数形式的9转化为浮点数形式,以pFloat表示
- 打印出整数n,遵循整型的存储规则,n肯定为9。
- 以浮点数的形式打印9,遵循浮点数的存储规则
-
9的补码为:00000000000000000000000000001001
-
浮点数存储:0 00000000 00000000000000000001001
-
表示:(-1)^0 × 0.00000000000000000001001×2(-126)=1.001×2(-146)=一个很小的数
-
我们知道float数是保留小数点后六位输出,所以输出0
4. n被改为浮点数9.0,以整数的方式打印,遵循整型的存储方式
-
浮点数:9.0表示成二进制为1001.0,即1.001*2^-3,表示为0 10000010 00100000000000000000000
-
整型打印:01000001000100000000000000000000——> 1091567616
-
浮点数以浮点数的形式打印,值为9.0
结言
愉快的数据的存储结束喽~嘻嘻