一、文章介绍
本文是针对吴飞教授在MOOC课程 :《人工智能:模型与算法》 2.1节 启发式搜索的课前发散

在课程2.1节 启发式搜索章节中,吴飞教授以如何计算城市地图两点之间最短路径为例,重点讲授了贪婪最佳优先搜索和A*搜索算法;但并未使用“笨办法”:遍历查询的方式来解决该需求,对于算法初学者来讲无法直观比较出搜索算法带来的效率提升。故本文目的在于通过遍历查询不借助任何算法,利用python内建数据结构与方法实现任意两点的所有可能路径及开销。
二、信息收集
根据课件,我们可以知晓以下信息:
- 城市地图
- 相邻城市的实际距离
地图如下:
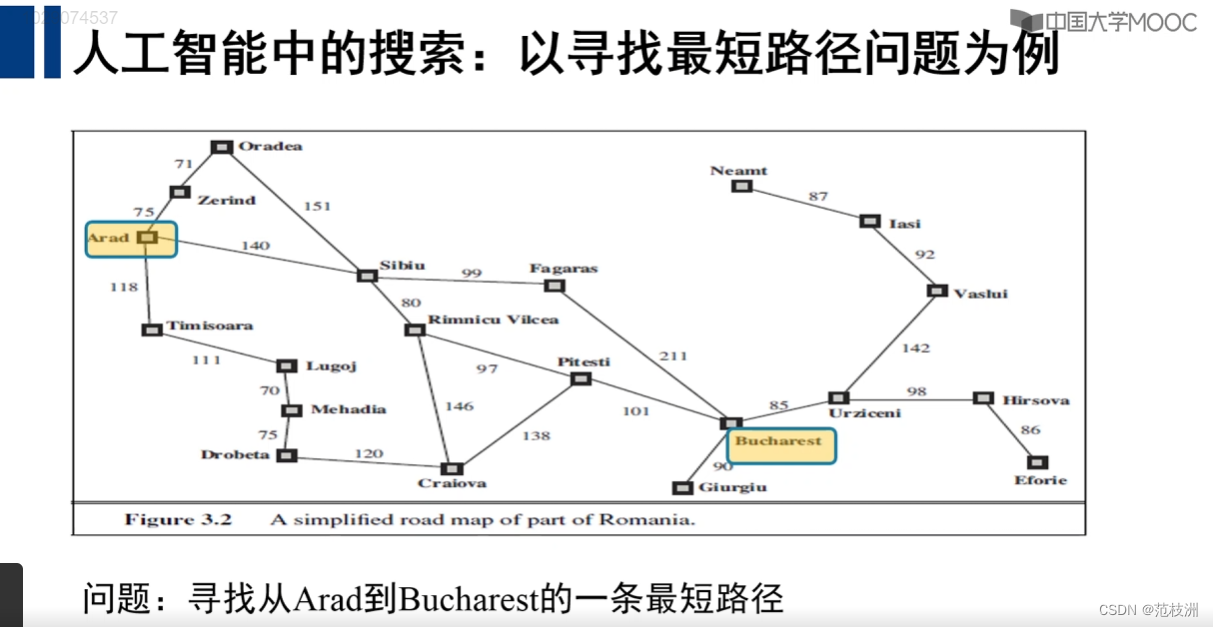
将以上信息录入python字典:
city_map = {'Arad':{'Zerind':75,'Sibiu':140,'Timisoara':118},
'Zerind':{'Oradea':71},
'Oradea':{'Sibiu':151},
'Timisoara':{'Lugoj':111},
'Lugoj':{'Mehadia':70},
'Mehadia':{'Drobeta':75},
'Drobeta':{'Craiova':120},
'Craiova':{'Pitesti':138},
'Sibiu':{'Fagaras':99,'Rimnicu Vilcea':80},
'Rimnicu Vilcea':{'Craiova':146,'Pitesti':97},
'Fagaras':{'Bucharest':211},
'Pitesti':{'Bucharest':101},
'Bucharest':{'Giurgiu':90,'Urziceni':85},
'Urziceni':{'Hirsova':98,'Vaslui':142},
'Hirsova':{'Eforie':86},
'Vaslui':{'Iasi':92},
'Iasi':{'Neamt':87},
}
问题1: 信息录入我们采取水平分割的录入方式,每个城市只录入下游相邻节点。 以Sibiu为例,其上游城市为Arad与Oradea; 但是并不录入,只录入Fagaras与Rimnicu Vilcea.
三、代码实现
3.1 数据处理
为了解决上述问题1,需要针对收集的城市数据进行处理,输出直观的全邻接信息。
# 统计city_map节点邻接关系
fullmesh_city_map={} # 用于记录全互联地图
# 遍历手工地图信息,正向解析下游城市
for k,v in city_map.items():
next_hop={}
for _k,_v in v.items():
next_hop[_k]=_v
if _k in city_map: # 逆向解析上游城市
if _k in fullmesh_city_map:
fullmesh_city_map[_k].update({k:_v})
else: #
fullmesh_city_map[_k] = {k:_v}
else: # 处理边界城市
fullmesh_city_map[_k] = {k:_v}
if k in fullmesh_city_map:
fullmesh_city_map[k].update(next_hop)
else:
fullmesh_city_map[k]=next_hop
# 打印
for k,v in fullmesh_city_map.items():
print(k,v)
输出结果如下:
Zerind {‘Arad’: 75, ‘Oradea’: 71}
Sibiu {‘Arad’: 140, ‘Oradea’: 151, ‘Fagaras’: 99, ‘Rimnicu Vilcea’: 80}
Timisoara {‘Arad’: 118, ‘Lugoj’: 111}
Arad {‘Zerind’: 75, ‘Sibiu’: 140, ‘Timisoara’: 118}
Oradea {‘Zerind’: 71, ‘Sibiu’: 151}
Lugoj {‘Timisoara’: 111, ‘Mehadia’: 70}
Mehadia {‘Lugoj’: 70, ‘Drobeta’: 75}
Drobeta {‘Mehadia’: 75, ‘Craiova’: 120}
Craiova {‘Drobeta’: 120, ‘Pitesti’: 138, ‘Rimnicu Vilcea’: 146}
Pitesti {‘Craiova’: 138, ‘Rimnicu Vilcea’: 97, ‘Bucharest’: 101}
Fagaras {‘Sibiu’: 99, ‘Bucharest’: 211}
Rimnicu Vilcea {‘Sibiu’: 80, ‘Craiova’: 146, ‘Pitesti’: 97}
Bucharest {‘Fagaras’: 211, ‘Pitesti’: 101, ‘Giurgiu’: 90, ‘Urziceni’: 85}
Giurgiu {‘Bucharest’: 90}
Urziceni {‘Bucharest’: 85, ‘Hirsova’: 98, ‘Vaslui’: 142}
Hirsova {‘Urziceni’: 98, ‘Eforie’: 86}
Vaslui {‘Urziceni’: 142, ‘Iasi’: 92}
Eforie {‘Hirsova’: 86}
Iasi {‘Vaslui’: 92, ‘Neamt’: 87}
Neamt {‘Iasi’: 87}
根据以上结果,可以发现任意城市都记录了上下游相邻城市。这便于后续代码的实现。
3.2 路径计算
本节代码用于计算任意两个给定城市间的可能路径和代价。因采用遍历的形式,且无任何标志用于判断程序是否已经得出两点之间的全部可能路径,故只能通过夸张的遍历次数来进行覆盖。
需求如下:
计算 城市’Oradea’与’Neamt’之间的可能路径与代价。
代码实现如下:
root = 'Oradea'
start = root
end = 'Neamt'
path = []
finnal_path=[]
times = 0
update_pop =[None]
while times<100000:
for k,v in fullmesh_city_map[start].items():
if update_pop[0] == None:
temp_path = [start,k,v]
path.append(temp_path)
else:
if k in update_pop:
path.append(update_pop)
else:
update_pop.insert(-1,k)
update_pop[-1] += v
path.append(update_pop)
update_pop=[]
for i in x_copy:
update_pop.append(i)
for x in path:
if x[-2] == end:
_a = []
for _x in x:
_a.append(_x)
if _a not in finnal_path:
finnal_path.append(_a)
else:pass
update_pop = path.pop(0)
x_copy = []
for i in update_pop:
x_copy.append(i)
start = update_pop[-2]
times+=1
# 打印结果
path_number = 1
for i in finnal_path:
print("线路{}: ".format(path_number),("--->".join(i[0:-1])),"距离 ",i[-1])
path_number += 1
经过计算,共有12条可选路径。
四、完整代码
以下代码运行后会出现12条可选路径。大家可自行验证。 自此,大家在学习玩搜索算法后方便感知算法的带来的效率改善情况。
city_map = {'Arad':{'Zerind':75,'Sibiu':140,'Timisoara':118},
'Zerind':{'Oradea':71},
'Oradea':{'Sibiu':151},
'Timisoara':{'Lugoj':111},
'Lugoj':{'Mehadia':70},
'Mehadia':{'Drobeta':75},
'Drobeta':{'Craiova':120},
'Craiova':{'Pitesti':138},
'Sibiu':{'Fagaras':99,'Rimnicu Vilcea':80},
'Rimnicu Vilcea':{'Craiova':146,'Pitesti':97},
'Fagaras':{'Bucharest':211},
'Pitesti':{'Bucharest':101},
'Bucharest':{'Giurgiu':90,'Urziceni':85},
'Urziceni':{'Hirsova':98,'Vaslui':142},
'Hirsova':{'Eforie':86},
'Vaslui':{'Iasi':92},
'Iasi':{'Neamt':87},
}
# 统计city_map节点邻接关系
fullmesh_city_map={} # 用于记录全互联地图
# 遍历手工地图信息,正向解析下游城市
for k,v in city_map.items():
next_hop={}
for _k,_v in v.items():
next_hop[_k]=_v
if _k in city_map: # 逆向解析上游城市
if _k in fullmesh_city_map:
fullmesh_city_map[_k].update({k:_v})
else: #
fullmesh_city_map[_k] = {k:_v}
else: # 处理边界城市
fullmesh_city_map[_k] = {k:_v}
if k in fullmesh_city_map:
fullmesh_city_map[k].update(next_hop)
else:
fullmesh_city_map[k]=next_hop
# 打印
for k,v in fullmesh_city_map.items():
print(k,v)
root = 'Oradea'
start = root
end = 'Neamt'
path = []
finnal_path=[]
times = 0
update_pop =[None]
while times<100000:
for k,v in fullmesh_city_map[start].items():
if update_pop[0] == None:
temp_path = [start,k,v]
path.append(temp_path)
else:
if k in update_pop:
path.append(update_pop)
else:
update_pop.insert(-1,k)
update_pop[-1] += v
path.append(update_pop)
update_pop=[]
for i in x_copy:
update_pop.append(i)
for x in path:
if x[-2] == end:
_a = []
for _x in x:
_a.append(_x)
if _a not in finnal_path:
finnal_path.append(_a)
else:pass
update_pop = path.pop(0)
x_copy = []
for i in update_pop:
x_copy.append(i)
start = update_pop[-2]
times+=1
# 打印结果
path_number = 1
for i in finnal_path:
print("线路{}: ".format(path_number),("--->".join(i[0:-1])),"距离 ",i[-1])
path_number += 1