VINS-MONO拓展2----更快地makeHessian矩阵(p

1. 目标

完成大作业T2
在这里插入图片描述

作业提示：
在这里插入图片描述

多线程方法主要包括以下几种(参考博客)：

MPI(多主机多线程开发),
OpenMP(为单主机多线程开发而设计)
SSE(主要增强CPU浮点运算的能力)
CUDA
Stream processing,

之前已经了解过std::thread和pthread，拓展1中makeHessian使用的是p_thread，这次正好用这几种方法与p_thread进行对比。

1. OpenMP

1.1 简单介绍

并行计算变量，共享则无需声明，如果需要该变量在每个线程中不同，则需要声明为private，如下，计算img中各个pixel的颜色，x共享，但y每个线程独立，即每个线程单独处理一行，都从第0列开始处理。
线程的分配方式是顺序分配给所有核(core)，如果多于核的个数，则再从第0个核开始分配。
语法，大概为两种，一种是普通代码的多线程，另一种是循环的多线程：

//普通多线程
#pragma omp parallel private(shared_var, tid)
{
	related code
}

//多线程循环
#pragma omp parallel for private(y, tid)
	//循环的代码
	for(){
		for()//二层循环等，不是必须		
	}

//多线程结束，其它代码

1.2 快速上手

根据tutorial的实验代码：

#include <cstdio>
//#include "stdafx.h"
#include <omp.h>//需要的头文件

int main(int argc, char* argv[])
{
    // This statement should only print once
    printf("Starting Program!\n");

    int nThreads, tid;
    int shared_var = 200000;
    int x,y;
    int width=3, height=3;
#pragma omp parallel for private(y, tid)
    for(x=0; x < height; x++)
    {
        for(y=0; y < width; y++)
        {
            tid = omp_get_thread_num();
            printf("thread: %d, x: %d, y: %d\n", tid, x, y);
        }
    }

    // We're out of the parallelized secion.
    // Therefor, this should execute only once
    printf("Finished!\n");

    return 0;
}

Cmakelists：

find_package(OpenMP REQUIRED)
add_executable(test_OpenMP OpenMP/test_OpenMP.cpp)
target_link_libraries(test_OpenMP PUBLIC OpenMP::OpenMP_CXX)

实验结果：
关于private的探究：
y为共享：
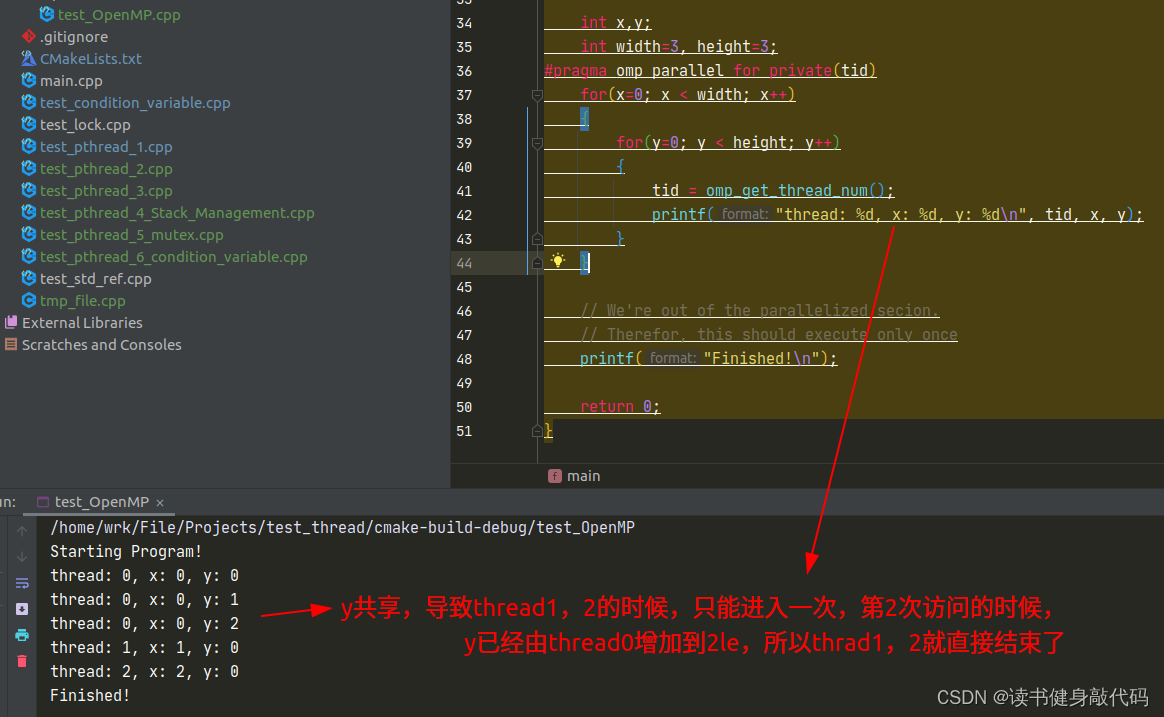
在这里插入图片描述

y为private
在这里插入图片描述

所以tutorial中的例程，意义是利用OpenMp多线程处理一张图片中的每一行，从每行的第0列开始处理：
在这里插入图片描述

for中线程的分配：
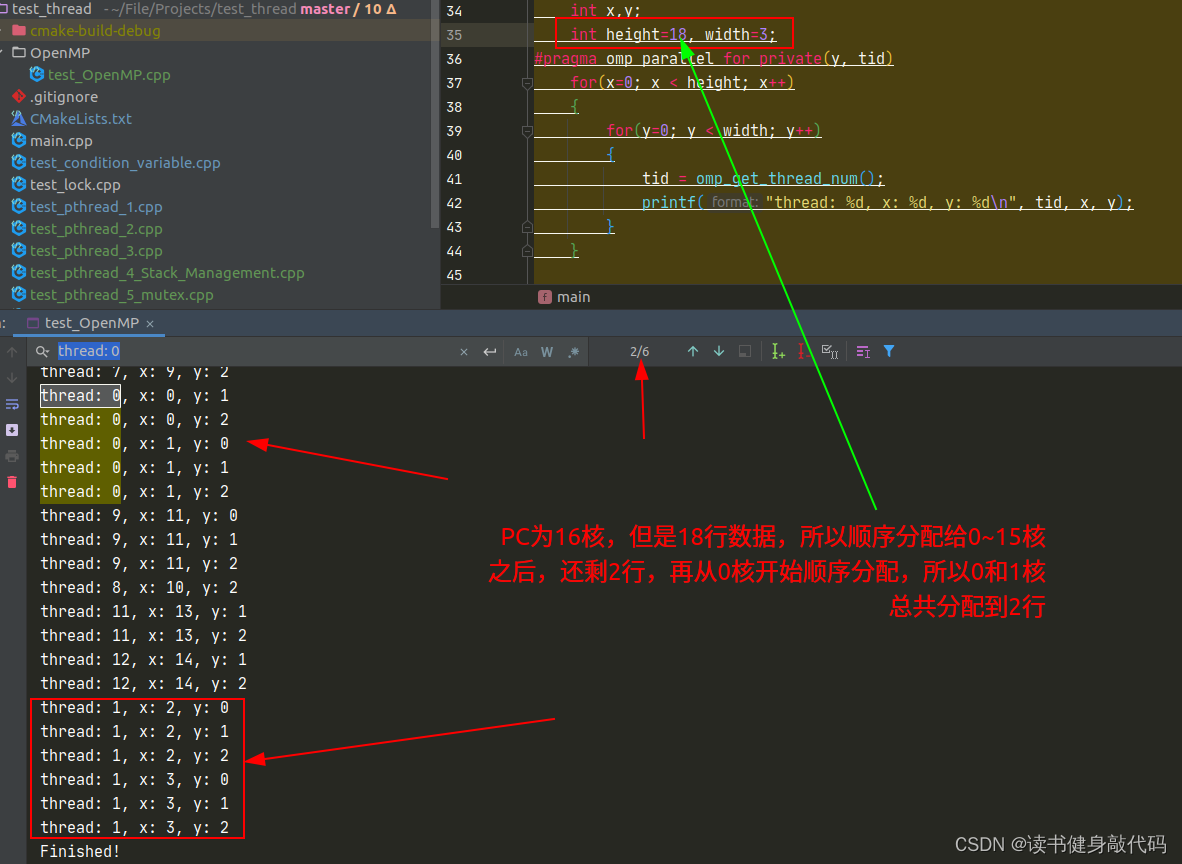
在这里插入图片描述

1.3 VINS-MONO移植

VINS-MONO中已经提供了pthread多线程和单线程makeHessian的方法，了解了OpenMP之后，我们需要使用单线程的方法，并告诉编译器使用OpenMP来进行，makeHessian代码如下：

void Solver::makeHessian()
{
    int pos = 0;//Hessian矩阵整体维度
    //it.first是要被marg掉的变量的地址,将其size累加起来就得到了所有被marg的变量的总localSize=m
    //marg的放一起，共m维，remain放一起，共n维
    for (auto &it : parameter_block_idx)
    {
        it.second = pos;//也算是排序1
        pos += localSize(parameter_block_size[it.first]);//PQ7为改为6维
    }

    m = pos;//要被marg的变量的总维度

    int tmp_n = 0;
    //与[0]相关总维度
    for (const auto &it : parameter_block_size)
    {
        if (parameter_block_idx.find(it.first) == parameter_block_idx.end())//将不在drop_set中的剩下的维度加起来，这一步实际上算的就是n
        {
            parameter_block_idx[it.first] = pos;//排序2
            tmp_n += localSize(it.second);
            pos += localSize(it.second);
        }
    }

    n = pos - m;//remain变量的总维度，这样写建立了n和m间的关系，表意更强
    ROS_DEBUG("\nn: %d, tmp_n: %d", n, tmp_n);

    ROS_DEBUG("\nSolver, pos: %d, m: %d, n: %d, size: %d", pos, m, n, (int)parameter_block_idx.size());

    TicToc t_summing;
    Eigen::MatrixXd A(pos, pos);//总系数矩阵
    Eigen::VectorXd b(pos);//总误差项
    A.setZero();
    b.setZero();
    Hessian_.resize(pos,pos);
    b_.resize(pos);
    delta_x_.resize(pos);

    //multi thread
    TicToc t_thread_summing;
    ROS_DEBUG("\nmulti thread: %s", MULTI_THREAD.c_str());
    if(MULTI_THREAD=="pthread") {
        pthread_t tids[NUM_THREADS];//4个线程构建
        //携带每个线程的输入输出信息
        ThreadsStruct threadsstruct[NUM_THREADS];
        //将先验约束因子平均分配到4个线程中
        int i = 0;
        for (auto it : factors)
        {
            threadsstruct[i].sub_factors.push_back(it);
            i++;
            i = i % NUM_THREADS;
        }
        //将每个线程构建的A和b加起来
        for (int i = 0; i < NUM_THREADS; i++)
        {
            TicToc zero_matrix;
            threadsstruct[i].A = Eigen::MatrixXd::Zero(pos,pos);
            threadsstruct[i].b = Eigen::VectorXd::Zero(pos);
            threadsstruct[i].parameter_block_size = parameter_block_size;//marg里的block_size，4个线程共享
            threadsstruct[i].parameter_block_idx = parameter_block_idx;
            int ret = pthread_create( &tids[i], NULL, ThreadsConstructA ,(void*)&(threadsstruct[i]));//参数4是arg，void*类型，取其地址并强制类型转换
            if (ret != 0)
            {
                ROS_WARN("pthread_create error");
                ROS_BREAK();
            }
        }
        //将每个线程构建的A和b加起来
        for( int i = NUM_THREADS - 1; i >= 0; i--)
        {
            pthread_join( tids[i], NULL );//阻塞等待线程完成，这里的A和b的+=操作在主线程中是阻塞的，+=的顺序是pthread_join的顺序
            A += threadsstruct[i].A;
            b += threadsstruct[i].b;
        }
    } else if(MULTI_THREAD=="openmp") {
        //OpenMP多线程
#pragma omp parallel for
        for(size_t k = 0; k < factors.size(); ++k) { // for (auto it : factors){
            ResidualBlockInfo* it = factors[k];
            //J^T*J
            for (int i = 0; i < static_cast<int>(it->parameter_blocks.size()); i++)
            {
                int idx_i = parameter_block_idx[reinterpret_cast<long>(it->parameter_blocks[i])];//要被marg的second=0
                int size_i = localSize(parameter_block_size[reinterpret_cast<long>(it->parameter_blocks[i])]);
                Eigen::MatrixXd jacobian_i = it->jacobians[i].leftCols(size_i);//remain变量的初始jacobian
                for (int j = i; j < static_cast<int>(it->parameter_blocks.size()); j++)
                {
                    int idx_j = parameter_block_idx[reinterpret_cast<long>(it->parameter_blocks[j])];
                    int size_j = localSize(parameter_block_size[reinterpret_cast<long>(it->parameter_blocks[j])]);
                    Eigen::MatrixXd jacobian_j = it->jacobians[j].leftCols(size_j);//marg变量的初始jacobian
                    //主对角线，注意这里是+=，可能之前别的变量在这个地方已经有过值了，所以要+=
                    if (i == j)
                        A.block(idx_i, idx_j, size_i, size_j) += jacobian_i.transpose() * jacobian_j;
                        //非主对角线
                    else
                    {
                        A.block(idx_i, idx_j, size_i, size_j) += jacobian_i.transpose() * jacobian_j;
                        A.block(idx_j, idx_i, size_j, size_i) = A.block(idx_i, idx_j, size_i, size_j).transpose();
                    }
                }
                b.segment(idx_i, size_i) += jacobian_i.transpose() * it->residuals;//J^T*e
            }
//            ROS_DEBUG("\nTotal number of threads: %d\n", omp_get_num_threads());
        }

    }
    //统计multi thread makeHessian时间
    double pure_finish_time = t_thread_summing.toc();
    *pure_makeHessian_time_sum_ += pure_finish_time;
    ++(*pure_makeHessian_times_);
    ROS_DEBUG("\nt_thread_summing cost: %f ms, avg_pure_makeHessian_time: %f ms, pure_makeHessian_time_sum_: %f, pure_makeHessian_times_: %f",
              t_thread_summing.toc(), (*pure_makeHessian_time_sum_)/(*pure_makeHessian_times_), *pure_makeHessian_time_sum_, *pure_makeHessian_times_);

    Hessian_ = A;
    b_ = -b;

    //DOGLEG需反解出J和e
    if(method_==solve::Solver::kDOGLEG) {
        TicToc t_solve_J;
        TicToc t_SelfAdjoint;
        Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes2(A);//这一句24.3ms
        ROS_DEBUG("\nt_SelfAdjoint cost: %f ms", t_SelfAdjoint.toc());
        Eigen::VectorXd S = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array(), 0));
        Eigen::VectorXd S_sqrt = S.cwiseSqrt();//开根号
        linearized_jacobians = S_sqrt.asDiagonal() * saes2.eigenvectors().transpose();
        Eigen::VectorXd S_inv = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array().inverse(), 0));
        Eigen::VectorXd S_inv_sqrt = S_inv.cwiseSqrt();
        linearized_residuals = S_inv_sqrt.asDiagonal() * saes2.eigenvectors().real().transpose() * b;
        ROS_DEBUG("\nt_solve_J cost: %f ms", t_solve_J.toc());//25ms
    }
}

其中注意for循环的写法，OpenMP似乎只支持for(int i=0; i<10; ++i)这种类型的循环，使用
for(auto i t :factors)这种写法则编译不过。

实验发现，openmp makeHessian的精度可能比pthread差，查看原因是 $\rho$ 经常 $< 0$ ，怀疑Hessian精度问题。makeHessian的时间跟Hessian的稠密程度也有关，发散时的makeHessian速度也很快，因为非常稀疏。所以对makeHessian速度的对比需要在收敛的情况下进行。

1.4 pthread与OpenMP对比

对比实验结果如下，倾向于使用pthread：
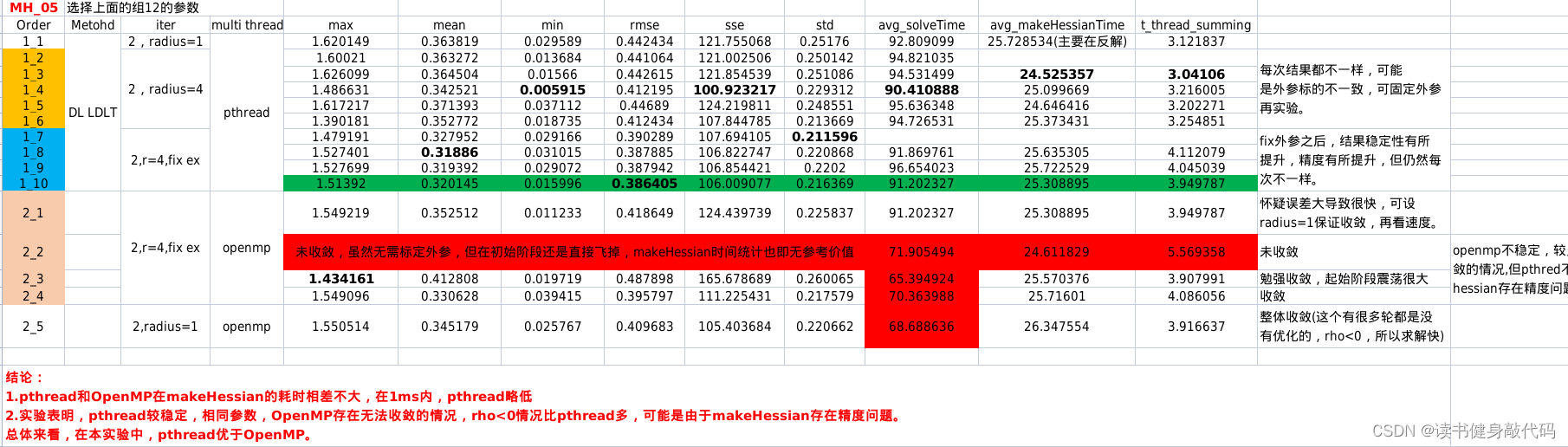
在这里插入图片描述

2024.1.9更新

关于每次优化结果不相同，在《Square Root Bundle Adjustment for Large-Scale Reconstruction》这篇文章中可能找到了一些原因：LM和DL频繁地rollback会导致 round-off errors，进而导致Schur complimnt based方法数值不稳定。而SBA这篇文章的 $\sqrt{BA}$ 方法一直很稳定（不确定是否每次优化结果相同。）
在这里插入图片描述

2. SSE

SSE 的指令集是 X86 架构 CPU 特有的，对于 ARM 架构、MIPS 架构等 CPU
是不支持的，所以使用了 SSE 指令集的程序，是不具备可移植标准的。而移动机器人平台
使用的 CPU 大多为了保证低功耗采用了 ARM 架构，所以这样的加速在移动机器人平台上
会失效。

大概看了下SSE的用法，如果需要用SSE，可能需要大改VINS-MONO中的数据结构，有些不划算，暂不考虑。

3. CUDA

参考文章

4. tbb

在复现21年CVPR square root BA过程中使用了tbb，特此记录。

以下大部分内容来自GPT3.5：

tbb::parallel_reduce 是 Intel 的 Threading Building Blocks（TBB）库中的一个算法，用于并行地执行可结合和可交换的二进制操作。它的主要目的是将一个可迭代的范围（比如一个数组或迭代器范围）的元素进行归约操作。

4.1 tbb::parallel_reduce用法简介

下面是 tbb::parallel_reduce 的基本用法：

#include <tbb/parallel_reduce.h>
#include <tbb/blocked_range.h>

// 定义一个结构体，用于存储并行归约的状态
template<typename T>
struct SumOperator {
    T sum;

    // 构造函数，初始化 sum
    SumOperator() : sum(0) {}

    // 归约操作
    void operator()(const tbb::blocked_range<T*>& range) {
        T local_sum = sum;
        for (T* i = range.begin(); i != range.end(); ++i) {
            local_sum += *i;
        }
        sum = local_sum;
    }

    // 合并操作，将两个状态合并
    void join(const SumOperator& other) {
        sum += other.sum;
    }
};

int main() {
    const int size = 1000;
    int data[size];

    // 初始化数据
    for (int i = 0; i < size; ++i) {
        data[i] = i;
    }

    // 定义并行归约的范围
    tbb::blocked_range<int*> range(data, data + size);

    // 创建归约对象
    SumOperator<int> sumOperator;

    // 使用 tbb::parallel_reduce 执行并行归约
    tbb::parallel_reduce(range, sumOperator);

    // 输出结果
    std::cout << "Sum: " << sumOperator.sum << std::endl;

    return 0;
}

在上述示例中，我们定义了一个 SumOperator 结构体，其中包含了归约的状态和相关的操作。在 main 函数中，我们首先初始化了一个数据数组，然后定义了一个 tbb::blocked_range 来表示归约的范围。接着，我们创建了一个 SumOperator 对象，并使用 tbb::parallel_reduce 来执行并行归约。最后，我们输出了结果。

SumOperator 结构体中的 operator() 函数定义了归约的操作，而 join 函数定义了两个状态如何合并。这两个函数是 tbb::parallel_reduce 算法所必需的。根据归约操作来定义相应的结构体和函数。

4.2 什么是规约?

在并行计算中，“规约”（Reduction）指的是将多个值合并成一个值的过程。典型的规约操作包括对一组数值进行求和、求平均值、找到最大或最小值等。规约在并行计算中非常重要，因为它可以将计算分散到多个处理单元，然后将结果合并成单个值。

在上下文中，规约的基本思想是将一个大问题分解成多个小问题，每个小问题在独立的处理单元上计算。然后，通过合并这些小问题的结果，得到整体问题的解。这种方法可以提高计算效率，特别是在大规模数据集或高性能计算环境中。

常见的规约操作有：

求和（Summation）：将一组数值相加得到总和。
求平均值（Average）：将一组数值相加后除以总数量得到平均值。
最大值（Maximum）和最小值（Minimum）：找到一组数值中的最大值或最小值。
位运算规约：对一组位进行操作，如按位与、按位或等。

在并行计算中，规约操作需要考虑同步和合并的问题，以确保正确性和性能。例如，归约操作中涉及的每个部分都需要在合并之前正确地完成计算，而合并的方式取决于具体的规约操作。

4.3 简单测试

计算 $\Sigma_{BEGIN}^{END}$ ，看多线程tbb和单线程谁更快：

#include <iostream>
#include <tbb/tbb.h>
#include "../Utility/tic_toc.h"

using Scalar = int64_t;

#define BEGIN 1
#define END 1e11


template<typename Scalar>
Scalar testTBB(void) {
    Scalar sum = tbb::parallel_reduce(
            tbb::blocked_range<size_t>(BEGIN,END),
            Scalar(0),
            [&](tbb::blocked_range<size_t> range, Scalar localSum) {
                for(Scalar i = range.begin(); i< range.end(); ++i) {
                    localSum += i;
                }
                return localSum;
                },
    std::plus<Scalar>()
        );
    return sum;
}

Scalar singleThread(void) {
    return [](Scalar begin, Scalar end){
        Scalar local_sum = 0;
        for(Scalar i=begin; i<end; ++i) {
            local_sum += i;
        }
        return local_sum;
    }(BEGIN, END);
}

int main(int argc, char** argv) {
    TicToc t_tbb;
    std::cout << "tbb sum result = " << testTBB<Scalar>() << ", cost " << t_tbb.toc() << " ms" << std::endl;

    TicToc t_single_thread;
    std::cout << "t_single_thread sum result = " << singleThread() << ", cost " << t_single_thread.toc() << " ms" << std::endl;
}

在这里插入图片描述

当数据很大时注意数据溢出问题，最好使用int64_t。

测试表明：中小规模问题其实单线程更快，tbb可能把时间都花在了Reduction上，而大规模问题，tbb更快，所以大规模求解问题可能更适合使用并行计算。

4.3 复现代码分析

/* 遍历每一个 landmark block，基于当前相机 pose 和特征点的 position 来预计算误差 r */
/* 同时，计算 vo problem 的整体误差 */
//this->sumCost = tbb::parallel_reduce(range, identity, real_body, reduction);,即 this->sumCost = 并行reduction( real_body(range, identity) )
template<typename Scalar>
bool ProblemVO<Scalar>::PrecomputeResidual(void) {
    this->sumCost = tbb::parallel_reduce(
            tbb::blocked_range<size_t>(0, landmarkBlocks.size()),// 参数1：迭代范围
            Scalar(0), // 参数2：初始值
            // 参数3：lambda 函数，定义局部操作
            [&] (tbb::blocked_range<size_t> range, Scalar localSum) {
                    for (size_t i = range.begin(); i < range.end(); ++i) {
                        this->landmarkBlocks[i]->PrecomputeResidual();
                        auto observes = this->landmarkBlocks[i]->GetObserves();
                        for (auto &ob : observes) {
                            // 这里计算的是每一个观测误差的带核函数的马氏距离，即 rho(r.T * S * r)
                            localSum += ob.second->kernel->y;
                        }
                    }
                    return localSum;
                },
            std::plus<Scalar>() // 参数4 Reduction：合并操作(同样还有std::minus<Scalar>, std::multiplies<Scalar>等reduction操作)
    );
    // std::cout << "this->sumCost is " << this->sumCost << std::endl;
    return true;
}

这段代码是一个用于预计算误差的函数，其中使用了 Threading Building Blocks (TBB) 库的 tbb::parallel_reduce 算法来并行地处理每个 landmark block 中的特征点观测误差。

主要步骤如下：

landmarkBlocks 是一组 landmark block 的集合，使用 tbb::parallel_reduce 并行处理每个 landmark block。这里，每个 landmark block 都调用了 PrecomputeResidual 函数，该函数用于预计算每个特征点的观测误差。
在每个 landmark block 中，通过 this->landmarkBlocks[i]->GetObserves() 获取该 landmark block 中的观测信息。
对于每个观测，计算观测误差的带核函数的马氏距离，即 $\rho(r^T*S*r)$ ，其中 $r$ 为观测误差，
$ρ$ 为核函数， $S$ 为权重矩阵。将每个观测误差的带核函数的马氏距离加到局部和 localSum 中。
tbb::parallel_reduce 最后将每个线程的局部和进行合并，最终得到整体的 sumCost。在此例中，sumCost 是所有观测误差的带核函数的马氏距离的总和。
函数返回 true 表示计算完成。

需要注意的是，由于使用了 TBB 的并行计算，每个线程可以独立地计算不同 landmark block 中的观测误差，提高了计算效率。最后通过 std::plus() 实现了对所有线程的局部和的合并，得到整体的误差和 sumCost。

tbb::parallel_reduce传参分析：

参数1：迭代范围 (tbb::blocked_range<size_t>(0, landmarkBlocks.size()))
这是一个描述迭代范围的对象，表示 landmarkBlocks 的索引范围。在这里，它表示了从0到 landmarkBlocks.size() 的范围。
参数2：初始值 (Scalar(0))
初始值用于初始化归约的结果。在这里，localSum 被初始化为 Scalar 类型的零值。
参数3：lambda 函数 ([&] (tbb::blocked_range<size_t> range, Scalar localSum) {...})
这是一个 lambda 函数，定义了并行操作的局部计算。它接收一个表示当前迭代范围的 tbb::blocked_range 对象和一个局部和 localSum，并在该范围上执行计算。lambda 函数的返回值是局部和，将被传递给合并操作。
参数4：合并操作 (std::plus<Scalar>())
这是一个函数对象，用于定义如何合并两个局部和。在这里，使用了 std::plus()，表示将两个 Scalar 类型的值相加。这个函数对象将被用于合并不同线程的局部和，得到整体的结果。

参数1和参数2分别传给lambda函数的两个参数，lambda函数的返回值是每个线程的返回值，参数4的Reduction操作将每个线程的返回值进行合并，所以整段代码可以这样理解：

this->sumCost = tbb::parallel_reduce(range, identity, real_body, reduction);
即
this->sumCost = 并行reduction( real_body(range, identity) );

4.4 tbb拓展

在debug时，tbb多线程打印出来的东西是乱序的，无法进行debug，所以前期可以设置为单线程先debug，保证代码单线程能正常运行后再开启多线程。

// 在 TBB 中，可以使用 tbb::global_control 类来设置线程数
tbb::global_control control(tbb::global_control::max_allowed_parallelism, 1);

// 获取机器上允许的最大并发线程数
int maxConcurrency = tbb::this_task_arena::max_concurrency();