保留几位小数的函数
方法一:
头文件
#include<iomanip>
格式
cout<<fixed<<setprecision(int n)<<a;
作用:把a保留三位小数
方法二:
还有一种方法,就是用C++从C语言保留的printf()方法。
保留二位小数:printf("%.2f", 数)
全排列函数
函数原型:
#include <algorithm>
bool next_permutation(iterator start,iterator end)
例子
#include <iostream> #include <algorithm> using namespace std; int main() { int num[3]={1,2,3}; do { cout<<num[0]<<" "<<num[1]<<" "<<num[2]<<endl; }while(next_permutation(num,num+3)); return 0; }
结果
当我们把while(next_permutation(num,num+3))中的3改为2时,输出就变为了:
next_permutation(num,num+n)函数是对数组num中的前n个元素进行全排列,同时并改变num数组的值。
next_permutation()在使用前需要对欲排列数组按升序排序,否则只能找出该序列之后的全排列数。比如,如果数组num初始化为2,3,1,那么输出就变为了:
反斜杠的作用
如何在输出语句中输出“”
反斜杠"\"后面的一个字符原样输出。
例如:
#include <stdio.h>
void main()
{
printf("\"hh\"");
return 0;
}输出结果是"hh"
如何在输出语句中输出 \
在 \ 后面再加一个 \
#include <stdio.h>
void main()
{
printf("\\");
return 0;
}结果是 \
结论1:若只输出反斜杠时,奇数个反斜杠输出编译不通过
若有如下代码
cout<<"\\n";输出结果为
\n结论2:转义字符 \\ 得到的 \ 不再参与组成新的转义字符
字符串中反斜杠\的特殊性
char a[10]="\0\0"; \0是转义字符,表示空格,又因为在字符串中,空格是字符串结束的标志,所以字符串a的长度是0。
char a[10]="\\0\0"; 第一个反斜杠后面还是反斜杠,\\ 是转义字符,表示一个反斜杠。 然后是字符0,再就是结束符 \0。 所以a表示的是字符串 \0
例子 s="abc"
比如说我们想定义一个带有双引号的字符串 s="abc";
- s="abc" 这样s输出是没有双引号的。
- s=" "abc" " 这样连编译都不通过
出现这个问题的原因是双引号原本就是表示字符串的边界的,所以处理起来格外棘手。
有了转义字符,直接在双引号前加上\, \" 就是一个表示双引号的转义字符,问题一下子就解决了。
s=" \" abc\" ";
二进制、八进制、十六进制的输入
1)二进制
二进制数字由 0 和 1 组成
以 0b / 0B 开头,不区分大小写(数字0,而非字母o,下同)
//正确的书写格式:
int a = 0b101; //表示十进制数字 5
int b = -0B110; //表示十进制数字 -62)八进制
八进制数字由 0~7 的数字组成
//正确的书写格式:
int a = 011; //表示十进制数字 9
int b = -0101; //表示十进制数字 -65
注意
//错误1 int c = 61; int d = 061; //c无前缀0,为十进制数字 61 //d为八进制数字 61,表示十进制下 49 //错误2 int x = 0A1; //A表示十六进制下的10 //并非八进制数字 //书写无效
3)十六进制
由数字 0~9 和字母 a~f (A~F)表示,不区分大小写
//正确的书写格式:
int a = 0xffff;//表示十进制数字 65535
int b = -0X1001;//表示十进制数字 -4097注意:
//错误1
int a = Aff1;
//没有引用 0x/0X 前缀
//此为无效书写
//错误2
int b = 0XafH;
//字母 H 不在 a~f 的范围内
//此为无效书写输出:
int main()
{
int n = 0;
printf("输入一个八进制数字:");
scanf("%o", &n);
printf("十进制为:%d\n", n);
printf("八进制为:%o\n", n);
printf("十六进制为:%x\n", n);
return 0;
}
// 输出
输入一个八进制数字:022
十进制为:18
八进制为:22
十六进制为:12求三角形面积的三种方法
鞋带公式
为什么叫做鞋带公式,这是因为在计算的过程很像鞋带一样缠绕着,
比如一个多边形(三角形),
三个顶点分别是 A:(x1, y1) , B:(x2, y2) , C:(x3, y3)
鞋带公式是这样子算的:
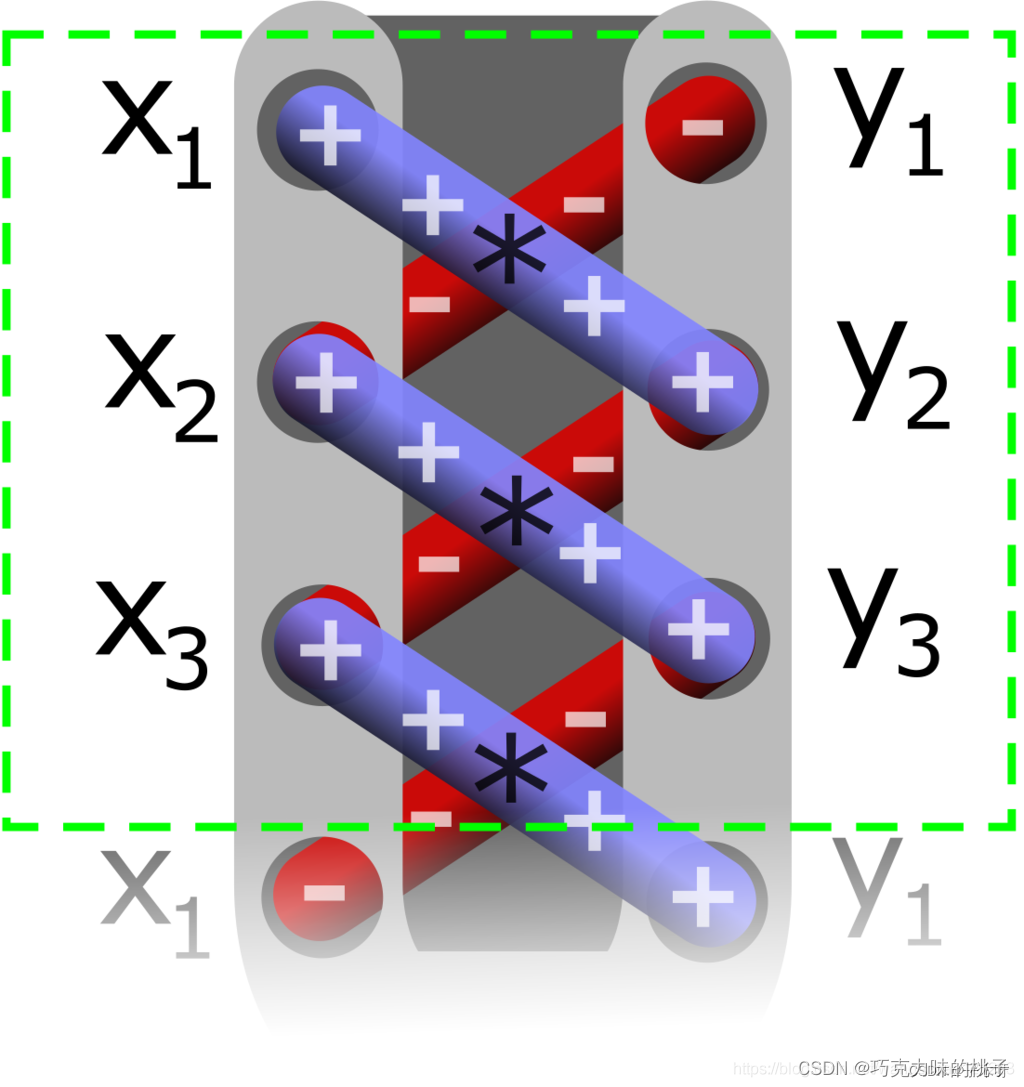
S三角形=0.5∗((x1∗y2+x2∗y3+x3∗y1)−(y1∗x2+y2∗x3+y3∗x1))
代个例子A:(0, 4) , B:(0, 0) , C:(3, 0) 到公式中:
S三角形=0.5∗((0∗0+0∗0+3∗4)−(4∗0+0∗3+0∗0))=6
在计算多边形面积的时候很方便。

首先参考一个例子,展示如何利用鞋带定理计算多边形面积。
我们只需选择一个顶点,然后按照逆时针顺序读取坐标,最后回到起点。
并按照类似系鞋带的顺序将坐标串联起来。
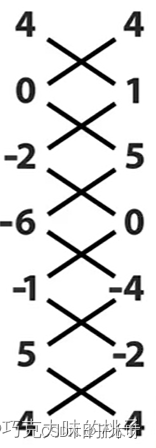
将绿线相连的数直接相乘,再相加;将红线相连的数直接相乘,再相加。最后将两者相减,则多边形的面积为110/2=55

海伦公式

而公式里的p为半周长(周长的一半):

三角形面积公式
S = 1/2 * a * b * sin(C)
首先得到两边的长度,通过叉积算出夹角的正弦值,并使用公式计算出面积。
求平方根
#include <bits/stdc++.h>
using namespace std;
int main(){
int n;
cin >> n;
// 求n的平方根
double r = sqrt(n);
cout << r << endl;
}
N次方如何表示
例如10的3次方
第一种方法:1e+3,10的-3次方则后面添上负号即1e-3,e前面必须要有数字。
第二种方法:利用函数pow(x,y);
即pow(10,3);注意要加上头文件cmath。