本篇博客将详细介绍数学建模的步骤。
文章目录
- 引例:年夜饭的准备
- 第一步:模型准备
- 第二步:模型假设
- 第三步:模型建立
- 第四步:模型求解
- 第五步:结果分析
- 第六步:模型检验
- 第七步:模型应用及推广
- 数学建模步骤总结
- 补充知识点——模型建立的方法
- 机理分析法
- 系统辨识建模法
- 仿真建模法
- 相似类比法
引例:年夜饭的准备
我们先来看一个例子。
假设小明家开始准备年夜饭,计划购买不同的食材和菜品。小明家希望尽量在有限的预算内,选择最佳的食材和菜品组合,以最大限度满足家庭成员的口味喜好,并提供充足的营养物质。
食材 价格(元**/**斤) 口味得分 营养得分 牛肉 40 40 30 鱼 30 30 15 鸡肉 25 25 12 鸡蛋 8 8 10 白菜 10 10 6 香菇 15 15 7 青菜 12 12 6 大米 5 5 3 家庭预算为800元,家庭成员口味得分最低要求为40,家庭成员营养得分最低要求为50。
这道题比较结合实际,毕竟还有一个月的时间就要过年了。那么大家如果能看懂这个例子的话,等过年自己家需要准备年夜饭的时候,可以跟父母说自己会用数学建模的知识解决咱家过年需要买什么菜的问题。
下面将从数学建模的角度进行求解。
第一步:模型准备
作为数学建模的第一步,我们首先要了解问题的实际背景,明确其实际意义,将实际问题翻译成数学问题。如果问题比较专业,必要时需要预先学习相关背景知识。然后将问题进行分解,分解成几个层次或者部分。最后判断解决该问题属于哪一类别,可能需要建立什么样的模型。
针对这个问题,解决步骤如下:
1、翻译成数学问题:求口味得分的最大值。
2、将问题分为几个部分:
购买食材的费用≤800
购买的食材口味得分≥40
购买的食材营养得分≥50
3、判断问题需要建立什么模型:因为是求最大值,所以这个题目属于优化类问题。同时只有一个目标函数,所以建立单目标优化模型。
由于这道题目比较简单,第二步其实也是可以认为是将实际问题翻译数学问题。而正常的数学建模竞赛的题目是比较复杂的,题目里可能既有优化,又有预测,还可能有评价,因此,此时应该要对题目进行分解。
看到这里,可能有人就会问,这道题可以设置成是两个目标函数吗,即求口味得分最大值和求营养得分最大值?
答案是可以的。这个题目本身也并没有明确说以什么为目标,也就是没有明确告诉要求什么变量达到最优。这种题目风格其实就是有一点点像美赛的题目风格。同学们可以不用完全把自己的思维限定在单目标优化上,也就是只有一个目标函数,是可以放飞自己的思路,只要合理即可。
第二步:模型假设
模型假设是指根据实际对象的特征和建模的目的,对问题进行必要的简化,并用精确的语言提出一些恰当的假设,从而保证模型的严密性。
注意:假设必须合理!
针对这个题目,我们给出以下假设:
假设一:假设食材的价格、口味得分和营养得分不发生变化。
假设二:假设购买食材的价格不会超过预算。
第三步:模型建立
模型建立是指在假设的基础上,利用适当的数学工具来刻画各变量常量之间的数学关系,建立相应的数学结构。
针对这个题目,我们建立如下模型:
(1)设定决策变量
设x1表示购买牛肉的数量(斤),x2表示购买鱼的数量(斤),x3表示购买鸡肉的数量(斤),x4表示购买鸡蛋的数量(斤),x5表示购买白菜的数量(斤),x6表示购买香菇的数量(斤),x7表示购买青菜的数量(斤),x8表示购买大米的数量(斤)。
(2)确定决策变量
最大化口味和营养的总和得分,即
其中, S i S_i Si代表第i个食材的口味得分。
(3)确定约束条件
综上,最终建立的模型如下:
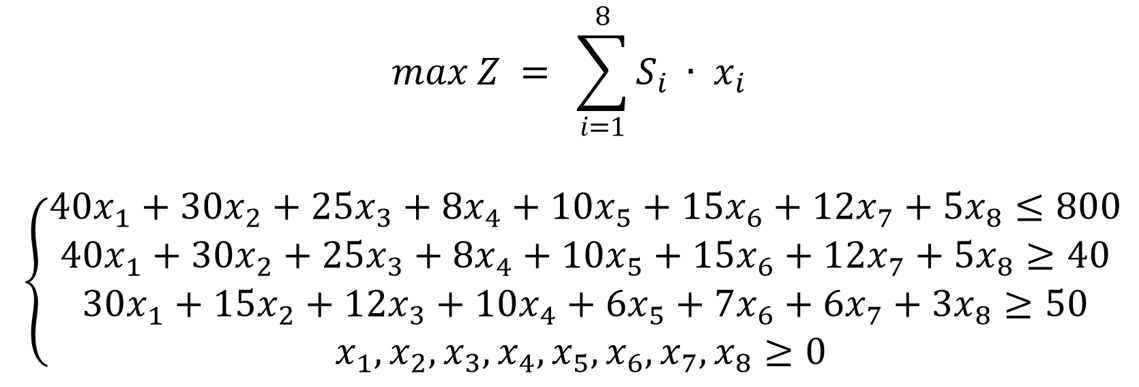
第四步:模型求解
模型求解方法有解方程,图解,定理证明,逻辑推理,编程计算,统计分析等。本模型运用MATLAB进行求解,代码如下:
clear all
clc
%% 定义目标函数的系数
c = [-40,-30,-25,-8,-10,-15,-12,-5];
%% 定义不等式约束矩阵
A = [
40,30,25,8,10,15,12,5; % 预算约束
-40,-30,-25,-8,-10,-15,-12,-5; % 口味得分约束
-30,-15,-12,-10,-6,-7,-6,-3 % 营养得分约束
];
%% 定义不等式约束右侧
b = [800;-40;-50];
%% 设置变量的边界
lb = zeros(8,1);
%% 使用linprog函数求解问题
options = optimoptions('linprog','Algorithm','interior-point'); % 选择算法
[x,fval,exitflag,output] = linprog(c,A,b,[],[],lb,[],options);
%% 输出结果
disp('最优解:');
disp(x);
disp('最优值(最大口味得分):');
disp(-fval);
第五步:结果分析
数学建模中常见的结果分析有:
(1)对结果进行误差分析,统计分析
(2)解释结果对实际问题的意义
(3)解释参数在实际问题中的作用
(4)对变量之间的依赖性、稳定性进行分析
(5)对模型进行评价、优化、甚至重新建模
针对本问题,运行MATLAB代码得到结果如下图所示:

因此,模型结果为买1.80斤的牛肉,5.50斤的鸡肉,3.52斤的鸡蛋,21.76斤的香菇,10.58斤的青菜,21.81斤的大米。
结果分析:荤素搭配,种类齐全,符合实际。
实际在写论文的时候,可以多写一点,这里仅仅是简要对结果进行分析。
第六步:模型检验
模型检验:模型检验在于评估建立的数学模型对实际问题的适用性和准确性,确保模型在应用中能够产生合理的结果。针对不同的模型,有不同的检验方法:残差分析、统计假设检验、灵敏度分析和模型比较等等。
本题所建立的模型使用灵敏度分析进行检验,以判断模型的稳定性。
灵敏度分析:控制其他参数不变的情况下,改变模型中某个重要参数的值。观察随着参数值的变化而导致的结果变化情况,判断输出受变化参数影响大小。
| 鱼肉口味得分变化 | 最优值变化 | 最优值变动幅度 |
|---|---|---|
| 33(+10%) | 880 | 10% |
| 30(0%) | 800 | 0% |
| 27(-10%) | 800 | 0% |
由于最优值变动幅度不超过决策变量的变动幅度,所以该模型较为稳定。
第七步:模型应用及推广
模型的应用因问题的性质和建模的目的而异,而模型的推广就是在现有模型的基础上对模型有一个更加全面的考虑,建立更符合现实情况的模型。
针对本题,我们可以将模型推广应用到生活中企业采购问题上。
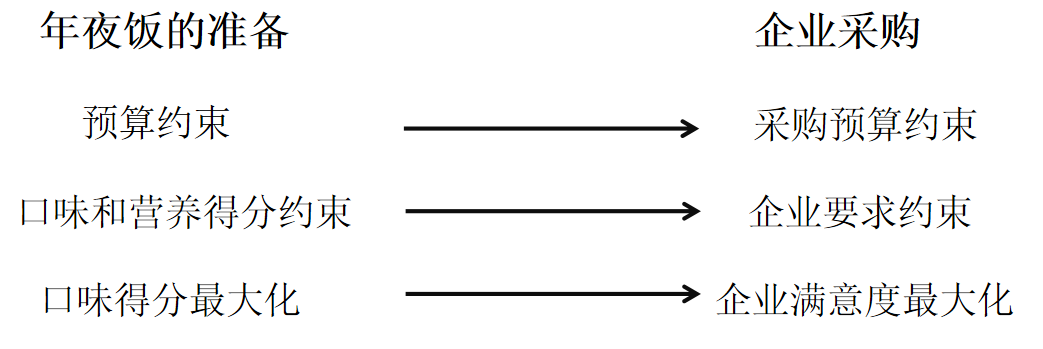
预算约束可以引申到采购预算约束,口味和营养得分约束可以引申到企业要求约束,口味得分最大化可以引申到企业满意度最大化。
数学建模步骤总结
几乎每一个数学建模题目,都离不开这七步:
(一)模型准备
(二)模型假设
(三)模型建立
(四)模型求解
(五)结果分析
(六)模型检验
(七)模型应用及推广
在今后的数学建模的过程中,同学们可以按照这七个步骤进行建模。
补充知识点——模型建立的方法
模型建立的常见方法有机理分析法、系统辨识建模法、仿真建模法和相似类比法。
机理分析法
机理分析法:机理分析是指对某个系统或现象的内部机制进行深入研究和分析的过程。它通常包括对系统或现象的结构、功能、过程、原理等方面的探究,以及对其背后的物理、化学、生物等基本规律的理解和解释。其核心思想是通过深入理解问题的物理或逻辑机制,建立数学模型来描述这种机制。例如,假设我们想要建立一个弹簧-阻尼系统的数学模型,我们可以通过分析弹簧的胡克定律和阻尼的牛顿定律,建立弹簧-阻尼系统的微分方程。这一步是通过机理分析理解弹簧和阻尼之间的物理关系,然后转化成数学形式。
系统辨识建模法
系统辨识建模法:系统辨识建模法是指从一系列实验数据中获取系统的数学模型,以了解和描述系统的行为。这个过程涉及对系统的结构和参数进行推断,以便用数学方程或模型来近似系统的行为。
假设有一个热水箱系统,我们希望建立一个数学模型,以描述水箱中水温随时间的变化。
(1)获取数据并对数据进行预处理。
(2)选择一个适当的数学模型结构,例如选择一个具有热容量、热传导和加热元件的动力学模型。
(3)进行参数估计。利用数学方法或原理,对所选模型结构中的参数进行估计,使得模型输出与实际观测数据最为一致。
(4)使用未参与参数估计的额外数据验证建立的模型在未知数据上的预测性能,对模型进行验证。
(5)根据验证结果,对模型进行优化。如果所选择的模型合适,则辨识结束;如果不合适,则改变第(2)步的数学模型结构,再次向下执行,直到获得一个比较满意的模型为止。
仿真建模法
仿真建模法:仿真建模法是数学建模中一种通过计算机模拟系统行为的方法。它通过建立数学模型,并使用计算机程序对模型进行求解,模拟系统在不同条件下的动态行为。
假设我们希望模拟城市交通流,以评估不同交通策略的效果。
(1)设计一个包含道路、车辆、信号灯等元素的交通模型,描述它们之间的相互作用。
(2)使用编程语言(例如Python、MATLAB)或专门的仿真工具将交通模型翻译为计算机可执行的代码。
(3)选择合适的仿真算法,以模拟交通流的动态变化。
(4)设定城市地图、车辆初始位置、交叉口信号灯控制策略等初始条件。运行仿真模型,模拟城市交通在不同时间段内的变化,包括车辆流量、拥堵情况等。
(5)分析仿真输出,评估不同交通策略对交通流的影响,从而为城市交通管理提供决策支持。
相似类比法
相似类比法:相似类比法是数学建模中的一种方法,它通过将一个复杂的系统映射到一个相对简单的系统,从而使得建模和分析变得更加可行。这种方法基于相似性原理,即两个系统在某些方面具有相似的特征,可以在某些方面进行类比。
假设某地区的生态系统因污染而受到影响,我们希望了解污染对该生态系统的影响。
(1)确定研究问题,即污染对该生态系统的影响。
(2)在其他领域中找到具有相似性质的已知模型,例如热力学中的热扩散模型。
(3)将热扩散模型适应于生态系统,将热传导的概念类比为污染物在生态系统中的传播,建立类比模型。
(4)通过实验或观测数据验证建立的类比模型是否能够合理地描述实际污染影响。
(5)若验证成功,则分析模型结果以及对模型进行拓展;若验证失败,则更换其他模型。
本篇博客到此结束!
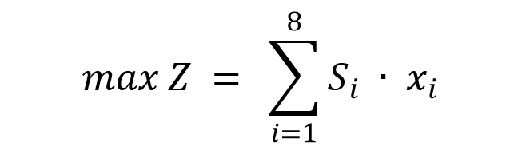
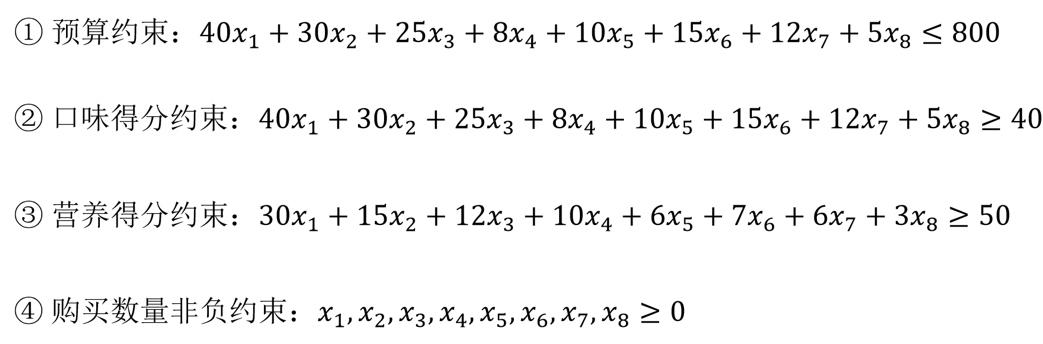








![buuctf[极客大挑战 2019]BabySQL--联合注入、双写过滤](https://img-blog.csdnimg.cn/img_convert/1e4e3e43bc63da5974db1263c270c6d2.png)

