隐马尔可夫模型(HMM)是一种统计模型,用于描述观测序列和隐藏状态序列之间的概率关系。它通常用于生成观测值的底层系统或过程未知或隐藏的情况,因此它被称为“隐马尔可夫模型”。
它用于根据生成数据的潜在隐藏过程来预测未来的观察结果或对序列进行分类。
HMM由两种类型的变量组成:隐藏状态和观测值。
- 隐藏状态是生成观测数据的基础变量,但它们不是直接可观测的。
- 观测值是被测量和观测的变量。
隐藏状态和观测值之间的关系使用概率分布建模。隐马尔可夫模型(HMM)是使用两组概率(转换概率和发射概率)来描述隐藏状态和观测值之间的关系。
- 转换概率描述了从一个隐藏状态转换到另一个隐藏状态的概率。
- 发射概率描述了在给定隐藏状态的情况下观察到输出的概率。
隐马尔可夫模型算法
隐马尔可夫模型(HMM)算法可以使用以下步骤来实现:
- 步骤1:定义状态空间和观测空间
状态空间是所有可能的隐藏状态的集合,观察空间是所有可能的观察的集合。 - 步骤2:定义初始状态分布
这是初始状态的概率分布。 - 步骤3:定义状态转移概率
这些是从一种状态转换到另一种状态的概率。这就形成了转移矩阵,它描述了从一种状态转移到另一种状态的概率。 - 步骤4:定义观测似然
这些是从每个状态生成每个观测的概率。这就形成了发射矩阵,它描述了从每个状态生成每个观测的概率。 - 步骤5:训练模型
使用Baum-Welch算法或前向-后向算法估计状态转移概率和观测似然的参数。这是通过迭代更新参数直到收敛来完成的。 - 步骤6:解码最可能的隐藏状态序列
给定观察到的数据,维特比算法用于计算最可能的隐藏状态序列。这可以用来预测未来的观察,分类序列,或检测序列数据中的模式。 - 步骤7:评估模型
HMM的性能可以使用各种度量来评估,例如准确度,精确度,召回率或F1分数。
总之,HMM算法涉及定义状态空间、观测空间以及状态转移概率和观测似然的参数,使用Baum-Welch算法或前向-后向算法训练模型,使用Viterbi算法解码最可能的隐藏状态序列,以及评估模型的性能。
Python中的实现及示例
使用hmmlearn库实现简单隐马尔可夫模型(HMM)的Python关键步骤。
示例1:预测天气
问题陈述:给定天气条件的历史数据,任务是根据当前天气预测第二天的天气。
1.导入所需的库
# import the necessary libraries
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from hmmlearn import hmm
2.定义模型参数
在这个例子中,状态空间被定义为一个状态,它是两个可能的天气条件的列表:“晴天”和“雨天”。观测空间被定义为观测,其是两个可能观测的列表:“干”和“湿”。隐藏状态的数量和观察的数量被定义为常数。
# Define the state space
states = ["Sunny", "Rainy"]
n_states = len(states)
print('Number of hidden states :',n_states)
# Define the observation space
observations = ["Dry", "Wet"]
n_observations = len(observations)
print('Number of observations :',n_observations)
输出
Number of hidden states : 2
Number of observations : 2
开始概率、转移概率和发射概率被定义为数组。开始概率表示在每个隐藏状态中开始的概率,转移概率表示从一个隐藏状态转移到另一个隐藏状态的概率,并且发射概率表示给定隐藏状态观察每个输出的概率。
初始状态分布被定义为state_probability,其是表示第一状态为“Sunny”或“Rainy”的概率的概率阵列。状态转换概率定义为transition_probability,它是一个2×2数组,表示从一个状态转换到另一个状态的概率。观测似然被定义为emission_probability,它是一个2×2数组,表示从每个状态生成每个观测的概率。
# Define the initial state distribution
state_probability = np.array([0.6, 0.4])
print("State probability: ", state_probability)
# Define the state transition probabilities
transition_probability = np.array([[0.7, 0.3],
[0.3, 0.7]])
print("\nTransition probability:\n", transition_probability)
# Define the observation likelihoods
emission_probability= np.array([[0.9, 0.1],
[0.2, 0.8]])
print("\nEmission probability:\n", emission_probability)
输出
State probability: [0.6 0.4]
Transition probability:
[[0.7 0.3]
[0.3 0.7]]
Emission probability:
[[0.9 0.1]
[0.2 0.8]]
3.创建HMM模型的实例并设置模型参数
HMM模型使用hmmlearn库中的hm.CategoricalHMM类定义。创建CategoricalHMM类的实例,将隐藏状态的数量设置为n_hidden_states,并使用startprob_、transmat_和emissionprob_属性将模型的参数分别设置为状态概率、转移概率和发射概率。
model = hmm.CategoricalHMM(n_components=n_states)
model.startprob_ = state_probability
model.transmat_ = transition_probability
model.emissionprob_ = emission_probability
4.定义观测序列
一个观测序列被定义为一个一维NumPy数组。
观察到的数据被定义为observations_sequence,它是一个整数序列,表示观察列表中的相应观察。
# Define the sequence of observations
observations_sequence = np.array([0, 1, 0, 1, 0, 0]).reshape(-1, 1)
observations_sequence
输出
array([[0],
[1],
[0],
[1],
[0],
[0]])
5.预测最可能的隐藏状态序列
隐状态的最可能的序列使用HMM模型的预测方法来计算。
# Predict the most likely sequence of hidden states
hidden_states = model.predict(observations_sequence)
print("Most likely hidden states:", hidden_states)
输出
Most likely hidden states: [0 1 1 1 0 0]
6.解码观察序列
Viterbi 算法用于计算最可能的隐藏状态序列,该隐藏状态序列使用模型的解码方法生成观察结果。该方法返回最可能的隐藏状态序列的对数概率和隐藏状态序列本身。
log_probability, hidden_states = model.decode(observations_sequence,
lengths = len(observations_sequence),
algorithm ='viterbi' )
print('Log Probability :',log_probability)
print("Most likely hidden states:", hidden_states)
输出
Log Probability : -6.360602626270058
Most likely hidden states: [0 1 1 1 0 0]
这是一个如何实现基本HMM并使用它来解码观察序列的简单算法。hmmlearn库提供了更先进、更灵活的Hondership实现,并提供了参数估计和训练等额外功能。
7.绘制结果
# Plot the results
sns.set_style("whitegrid")
plt.plot(hidden_states, '-o', label="Hidden State")
plt.xlabel('Time step')
plt.ylabel('Most Likely Hidden State')
plt.title("Sunny or Rainy")
plt.legend()
plt.show()
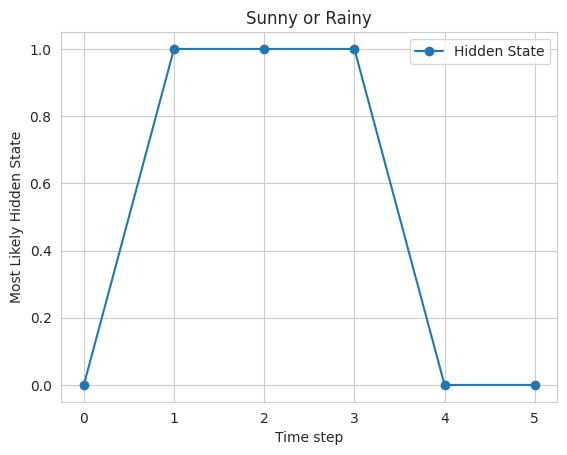
最后,使用matplotlib库绘制结果,其中x轴表示时间步长,y轴表示隐藏状态。该图显示,该模型预测的天气大部分是晴天,其中夹杂着一些雨天。
示例2:手写识别
问题陈述:给定一个手写字符的数据集,任务是根据字符的形状识别字符。
在这个例子中,状态空间被定义为状态,这是一个26个可能字符的列表。观察空间被定义为观察,其是8个可能的观察的列表,表示手写体中的笔划的方向。初始状态分布定义为start_probability,它是一个概率数组,表示第一个状态是26个字符中任何一个的概率。状态转换概率定义为transition_probability,它是一个26×26的数组,表示从一个字符转换到另一个字符的概率。观测似然度被定义为emission_probability,它是一个26×8的数组,表示从每个字符生成每个观测的概率。
HMM模型是使用hmmlearn库中的hmm.MultinomialHMM类定义的,模型的参数是使用模型对象的startprob_、transmat_和emissionprob_属性设置的。
观察序列定义为observations_sequence,是一个长度为11的数组,表示手写体中的11个笔画。模型对象的predict方法用于在给定观测值的情况下预测最可能的隐藏状态。结果存储在hidden_states变量中,该变量是一个长度为11的数组,表示每个笔划最可能的字符。
# import the necessary libraries
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from hmmlearn import hmm
# Define the state space
states = ["A", "B", "C", "D", "E", "F", "G", "H", "I", "J", "K", "L", "M",
"N", "O", "P", "Q", "R", "S", "T", "U", "V", "W", "X", "Y", "Z"]
n_states = len(states)
# Define the observation space
observations = ["up", "down", "left", "right", "up-right", "down-right",
"down-left", "up-left"]
n_observations = len(observations)
# Define the initial state distribution
start_probability = np.random.dirichlet(np.ones(26),size=(1))[0]
# Define the state transition probabilities
transition_probability = np.random.dirichlet(np.ones(26),size=(26))
# Define the observation likelihoods
emission_probability = np.random.dirichlet(np.ones(26),size=(26))
# Fit the model
model = hmm.CategoricalHMM(n_components=n_states)
model.startprob_ = start_probability
model.transmat_ = transition_probability
model.emissionprob_ = emission_probability
# Define the sequence of observations
observations_sequence = np.array([0, 1, 2, 1, 0, 1, 2, 3, 2, 1, 2]).reshape(-1, 1)
# Predict the most likely hidden states
hidden_states = model.predict(observations_sequence)
print("Most likely hidden states:", hidden_states)
# Plot the results
sns.set_style("whitegrid")
plt.plot(hidden_states, '-o', label="Hidden State")
plt.xlabel('Stroke')
plt.ylabel('Most Likely Hidden State')
plt.title("Predicted hidden state")
plt.legend()
plt.show()
输出
Most likely hidden states: [ 4 23 8 21 6 21 16 14 11 23 22]

最后,使用matplotlib中的plot函数绘制结果,该函数显示手写体中每个笔划的预测隐藏状态。
示例3:语音识别
问题陈述:给定音频记录的数据集,任务是识别录音中所说的单词。
在该示例中,状态空间被定义为状态,其是表示静音或3个不同单词之一的存在的4个可能状态的列表。观测空间被定义为观测,其是表示语音音量的2个可能观测的列表。初始状态分布被定义为start_probability,它是长度为4的概率数组,表示每个状态是初始状态的概率。
状态转移概率被定义为transition_probability,它是一个4×4矩阵,表示从一个状态转移到另一个状态的概率。观测似然被定义为emission_probability,它是一个4×2矩阵,表示每个状态发出观测的概率。
该模型使用hmmlearn库中的MultinomialHMM类定义,并使用startprob_、transmat_和emissionprob_属性拟合。观测序列定义为observations_sequence,是一个长度为8的数组,表示8个不同时间步长中的语音音量。
模型对象的predict方法用于在给定观测值的情况下预测最可能的隐藏状态。结果存储在hidden_states变量中,该变量是一个长度为8的数组,表示每个时间步最可能的状态。
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from hmmlearn import hmm
# Define the state space
states = ["Silence", "Word1", "Word2", "Word3"]
n_states = len(states)
# Define the observation space
observations = ["Loud", "Soft"]
n_observations = len(observations)
# Define the initial state distribution
start_probability = np.array([0.8, 0.1, 0.1, 0.0])
# Define the state transition probabilities
transition_probability = np.array([[0.7, 0.2, 0.1, 0.0],
[0.0, 0.6, 0.4, 0.0],
[0.0, 0.0, 0.6, 0.4],
[0.0, 0.0, 0.0, 1.0]])
# Define the observation likelihoods
emission_probability = np.array([[0.7, 0.3],
[0.4, 0.6],
[0.6, 0.4],
[0.3, 0.7]])
# Fit the model
model = hmm.CategoricalHMM(n_components=n_states)
model.startprob_ = start_probability
model.transmat_ = transition_probability
model.emissionprob_ = emission_probability
# Define the sequence of observations
observations_sequence = np.array([0, 1, 0, 0, 1, 1, 0, 1]).reshape(-1, 1)
# Predict the most likely hidden states
hidden_states = model.predict(observations_sequence)
print("Most likely hidden states:", hidden_states)
# Plot the results
sns.set_style("darkgrid")
plt.plot(hidden_states, '-o', label="Hidden State")
plt.legend()
plt.show()
输出
Most likely hidden states: [0 1 2 2 3 3 3 3]
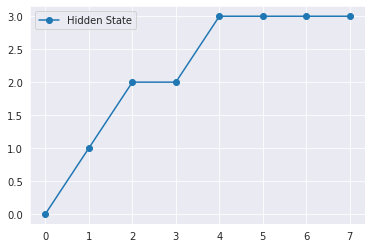
隐马尔可夫模型的其他应用
HMM被广泛用于各种应用,例如语音识别、自然语言处理、计算生物学和金融。例如,在语音识别中,HMM可以用于对生成语音信号的潜在声音或音素进行建模,并且观察可以是从语音信号中提取的特征。在计算生物学中,HMM可以用来模拟蛋白质或DNA序列的进化,观察结果可以是氨基酸或核苷酸的序列。
总结
总之,HMM是一个强大的工具,用于建模连续数据,其实现通过库,如hmmlearn,使他们的访问和有用的各种应用程序。