文章目录
- 十大排序算法
- 插入排序O(n^2^)
- 冒泡排序O(n^2^)
- 选择排序O(n^2^)
- 希尔排序——缩小增量排序O(nlogn)
- 快速排序O(nlogn)
- 堆排序O(nlogn)
- 归并排序(nlogn)
- 计数排序O(n+k)
- 基数排序O(n*k)
- 桶排序O(n+k)
十大排序算法
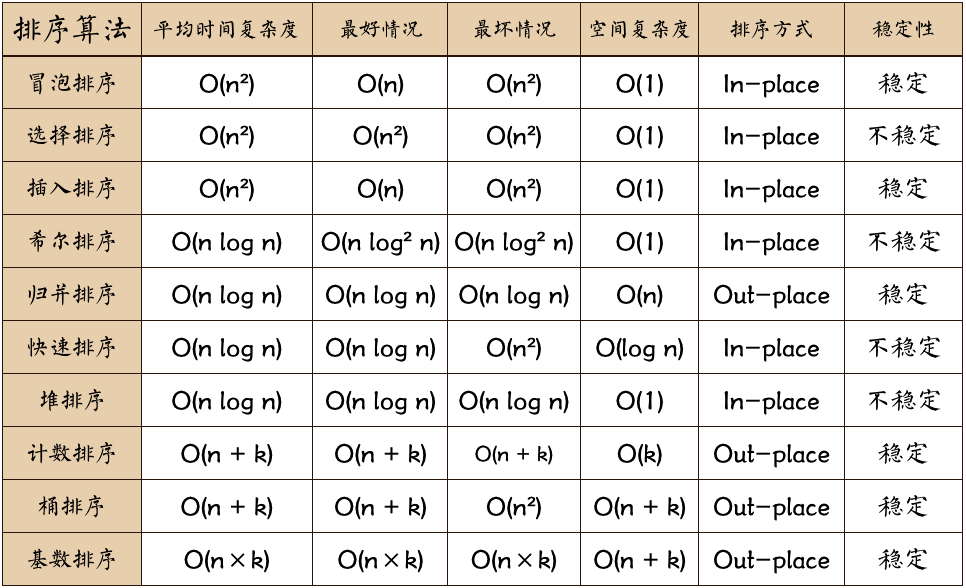
排序算法的稳定性:在具有多个相同关键字的记录中,若经过排序这些记录的次序保持不变,说排序算法是稳定的。
插入排序O(n2)
-
直接插入排序
动画演示如图:
代码如下:
void Straight_Insertion_Sort(int a[], int length)
{
for (int i = 1; i < length; i++)
{
if (a[i] < a[i - 1])
{
int temp = a[i];
for (int j = i - 1; j >= 0; j--)
{
a[j + 1] = a[j];
if (a[j] < temp)
{
a[j + 1] = temp;
break;
}
if (j == 0 && a[j] > temp)
{
a[j] = temp;
}
}
}
}
}
-
折半插入排序
主要分为查找和插入两个部分
图片演示:

代码如下:
void Binary_Insert_Sort(int a[], int length)
{
int low, high, mid;
int i, j, temp;
for (i = 1; i < length; i++)
{
low = 0;
high = i - 1;
temp = a[i];
while (low <= high)
{
mid = (low + high) / 2;
if (temp < a[mid])
{
high = mid - 1;
}
else
{
low = mid + 1;
}
} // while
for (j = i - 1; j > high; j--)
{
a[j + 1] = a[j];
}
a[j + 1] = temp;
} // for(i)
}
冒泡排序O(n2)
思路:两两比较元素,顺序不同就交换
图解:
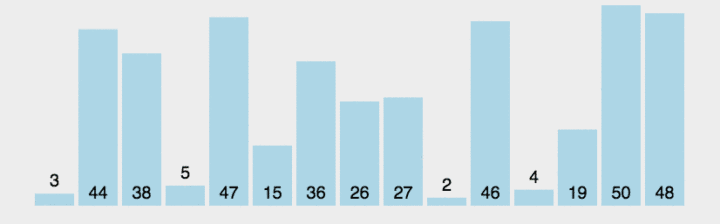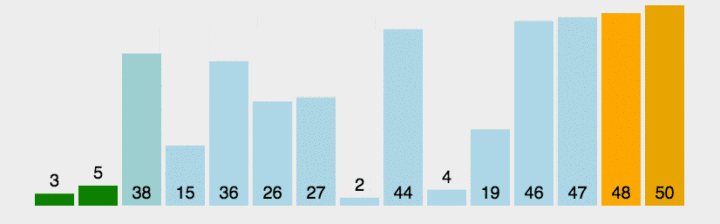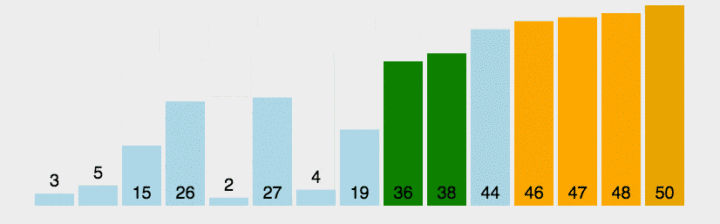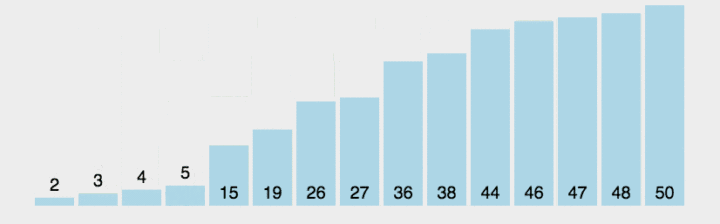
代码:
void Bubble_Sort(int a[], int length)
{
for (int i = 0; i < length - 1; i++)
{
for (int j = 0; j < length - i - 1; j++)
{
if (a[j] > a[j + 1])
{
int temp = a[j];
a[j] = a[j + 1];
a[j + 1] = temp;
}
}
}
}
选择排序O(n2)
思路:每一次从待排序的数据元素中选择最小(最大)的一个元素作为有序的元素。如果是升序排序,则每次选择最小值就行,这样已经排好序的部分都是生序排序选择排序是不稳定的,比如说(55231这种情况,两个5的相对顺序会变)
图解:
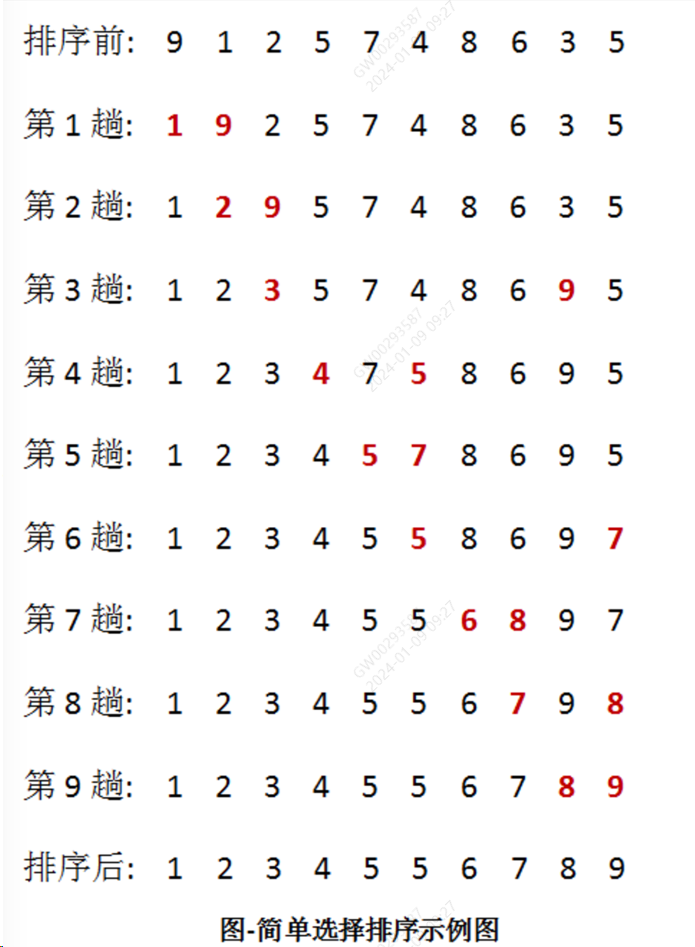
代码:
void Select_Sort(int a[], int length)
{
for (int i = 0; i < length - 1; i++)
{
int min_index = i;
for (int j = i + 1; j < length; j++)
{
if (a[min_index] > a[j])
{
min_index = j;
}
} // for j
if (i != min_index)
{
int temp = a[i];
a[i] = a[min_index];
a[min_index] = temp;
}
} // for i
}
希尔排序——缩小增量排序O(nlogn)
思路:
希尔排序又叫缩小增量排序,使得待排序列从局部有序随着增量的缩小编程全局有序。当增量为1的时候就是插入排序,增量的选择最好是531这样间隔着的。
其实这个跟选择排序一样的道理,都是不稳定的比如下图7变成9的话,就是不稳定的
图解:
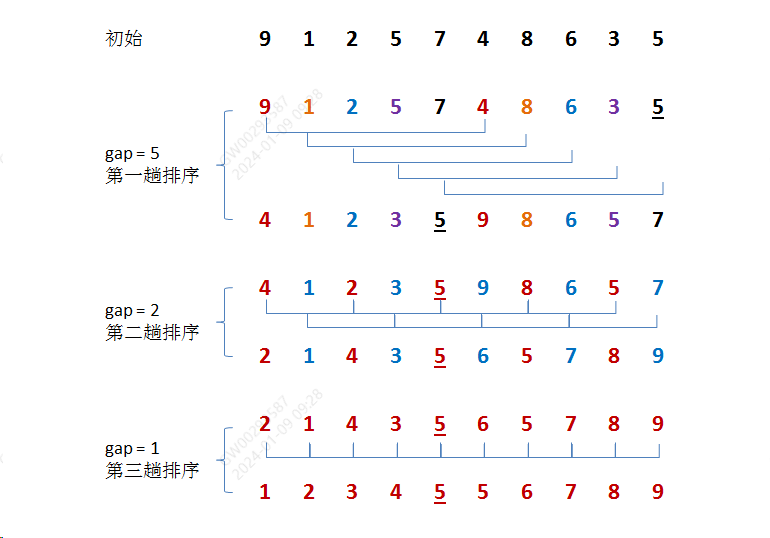
代码:
void Shell_Sort1(int a[], int length)
{
// 首先定义一个初始增量,一般就是数组长度除以2或者3
int gap = length / 2;
while (gap >= 1)
{
for (int i = gap; i < length; i++)
{
int temp = a[i];
int j = i;
while (j >= gap && temp < a[j - gap])
{
a[j] = a[j - gap];
j = j - gap;
} // while
a[j] = temp;
} // for
gap = gap / 2;
} // while
}
/*****************另一种写法, 好理解****************************/
void shellsort3(int a[], int n)
{
int i, j, gap;
for (gap = n / 2; gap > 0; gap /= 2)
for (i = gap; i < n; i++)
/*j>gap之后,j前面的可以重新比较依次保证j前面间隔gap的也是有序的*/
for (j = i - gap; j >= 0 && a[j] > a[j + gap]; j -= gap)
Swap(a[j], a[j + gap]);
}
快速排序O(nlogn)
思路:快排的核心叫做“基准值“,小于基准值的放在左边,大于基准值的放在右边。然后依次递归。基准值的选取随机的,一般选择数组的第一个或者数组的最后一个,然后又两个指针low和high
图解:“基准值就是第一个元素”
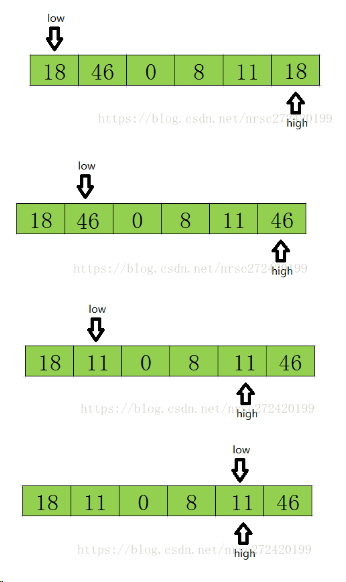
1)设置两个变量I、J,排序开始的时候:I=0,J=N-1;
2)以第一个数组元素作为关键数据,赋值给 key ,即 key =A[0];
3)从J开始向前搜索,即由后开始向前搜索(J=J-1即J–),找到第一个小于 key 的值A[j],A[j]与A[i]交换;
4)从I开始向后搜索,即由前开始向后搜索(I=I+1即I++),找到第一个大于 key 的A[i],A[i]与A[j]交换;
5)重复第3、4、5步,直到 I=J; (3,4步是在程序中没找到时候j=j-1,i=i+1,直至找到为止。找到并交换的时候i, j指针位置不变。另外当i=j这过程一定正好是i+或j-完成的最后另循环结束。)
代码:
// 快速排序 需要两个函数配合
int Quick_Sort_GetKey(int a[], int low, int high)
{
int temp = a[low];
while (low < high)
{
// 首先比较队尾的元素和关键之temp,如果队尾大指针就往前移动
while (low < high && a[high] >= temp)
{
high--;
}
// 当a[high]<temp的时候,跳出循环然后将值付给a[low],a[low]=temp
a[low] = a[high];
// 赋值过一次之后就立刻从队首开始比较
while (low < high && a[low] <= temp)
{
low++;
}
a[high] = a[low];
} // while (low<high)
a[low] = temp; // 或者a[high]=temp
return low;
}
void Quick_Sort(int a[], int low, int high)
{
if (low < high)
{
int key = Quick_Sort_GetKey(a, low, high);
Quick_Sort(a, low, key - 1);
Quick_Sort(a, key + 1, high);
}
}
堆排序O(nlogn)
思路:堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。堆排序分为两步:首先将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。随后第二步将其与末尾元素进行交换,此时末尾就为最大值。然后将这个堆结构映射到数组中后,就会变成升序状态了。(即升序—大根堆)
当数组元素映射成为堆时:
- 父结点索引:(i-1)/2
- +左孩子索引:2**i*+1
- 左孩子索引:2**i*+2
图解:

基本思想:
- 首先将待排序的数组构造成一个大根堆,此时,整个数组的最大值就是堆结构的顶端
- 将顶端的数与末尾的数交换,此时,末尾的数为最大值,剩余待排序数组个数为n-1
- 将剩余的n-1个数再构造成大根堆,再将顶端数与n-1位置的数交换,如此反复执行,便能得到有序数组
代码:
// index是第一个非叶子节点的下标(根节点)
// 递归的方式构建
void Build_Heap(int a[], int length, int index)
{
int left = 2 * index + 1; // index的左子节点
int right = 2 * index + 2; // index的右子节点
int maxNode = index; // 默认当前节点是最大值,当前节点index
if (left < length && a[left] > a[maxNode])
{
maxNode = left;
}
if (right < length && a[right] > a[maxNode])
{
maxNode = right;
}
if (maxNode != index)
{
int temp = a[maxNode];
a[maxNode] = a[index];
a[index] = temp;
Build_Heap(a, length, maxNode);
}
}
void Heap_Sort(int a[], int length)
{
// 构建大根堆(从最后一个非叶子节点向上)
// 注意,最后一个非叶子节点为(length / 2) - 1
for (int i = (length / 2) - 1; i >= 0; i--)
{
Build_Heap(a, length, i);
}
for (int i = length - 1; i >= 1; i--)
{
// 交换刚建好的大顶堆的堆顶和堆末尾节点的元素值,
int temp = a[i];
a[i] = a[0];
a[0] = temp;
// 交换过得值不变,剩下的重新排序成大顶堆
Build_Heap(a, i, 0);
}
}
归并排序(nlogn)
思路:分治思想,将若干个已经排好序的子序合成有序的序列。
图解:
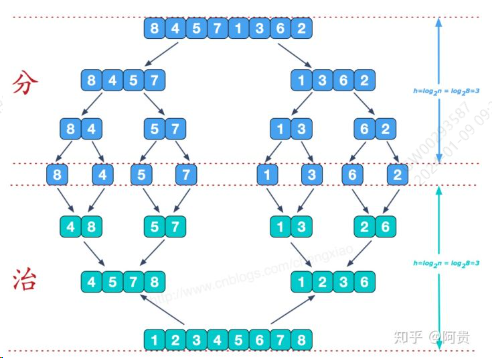
代码:
// 分治思想,先逐步分解成最小(递归)再合并
// 归并
void Merge(int a[], int low, int mid, int high)
{
int i = low;
int j = mid + 1;
int k = 0;
int* temp = new int[high - low + 1];
while (i <= mid && j <= high)
{
if (a[i] <= a[j])
{
temp[k++] = a[i++];
}
else
{
temp[k++] = a[j++];
}
} // while (i<mid&&j<=high)
while (i <= mid)
{
temp[k++] = a[i++];
}
while (j <= high)
{
temp[k++] = a[j++];
}
for (i = low, k = 0; i <= high; i++, k++)
{
a[i] = temp[k];
}
delete[] temp;
}
// 递归分开
void Merge_Sort(int a[], int low, int high)
{
if (low < high)
{
int mid = (low + high) / 2;
Merge_Sort(a, low, mid);
Merge_Sort(a, mid + 1, high);
cout << "mid=" << mid << " " << a[mid] << endl;
cout << "low=" << low << " " << a[low] << endl;
cout << "high=" << high << " " << a[high] << endl;
cout << endl;
// 递归之后再合并
Merge(a, low, mid, high);
}
}
代码看不懂没关系,参考链接
计数排序O(n+k)
思路:
将待排序的数据存放到额外开辟的空间中。首先找出元素的最大最小值,然后统计每个元素i出现的次数,然后放入数组i中,数组中存放的是值为i的元素出现的个数。额外数组中第i个元素是待排序数组中值为i的元素的个数。因为要求输入的数有确定范围,同时只能对整数进行排序,有场景限制。
图解:

代码:
void Count_Sort(int a[], int length)
{
// 得到待排序的最大值
int max = a[0];
int i = 0;
while (i < length - 1)
{
max = (a[i] > a[i + 1]) ? a[i] : a[i + 1];
i++;
}
int* countArray = new int[max + 1] { 0 };
int* temp = new int[length];
for (int i = 0; i < length; i++)
{
countArray[a[i]]++;
}
//!!!这一步的思想特别重要,在非比较排序中
for (int i = 1; i < max + 1; i++)
{
countArray[i] += countArray[i - 1];
}
// 反向遍历
for (int i = length - 1; i >= 0; i--)
{
temp[countArray[a[i]] - 1] = a[i];
countArray[a[i]]--;
}
for (int i = 0; i < length; i++)
{
a[i] = temp[i];
}
delete[] countArray;
delete[] temp;
}
基数排序O(n*k)
思路: 基数也就表明桶的个数是定死的,就是10个。基数排序的思想是,从个位依次开始排序,首先按照个位的大小排序,将改变的序列按照十位开始排序,然后一次往后……
图解:

代码:
int Get_Max_Digits(int a[], int length)
{
int max = a[0];
int i = 0;
while (i < length - 1)
{
max = (a[i] > a[i + 1]) ? a[i] : a[i + 1];
i++;
}
int b = 0; // 最大值的位数
while (max > 0)
{
max = max / 10;
b++;
}
return b;
}
// 切记!桶子只能是十个,是定死的
void Radix_Sort(int b[], int length)
{
int d = Get_Max_Digits(b, length); // 得到最大值的位数
int* temp = new int[length]; // 开辟一个和原数组相同的临时数组
// 根据最大值的位数进行排序次数循环
int radix = 1;
for (int i = 0; i < d; i++)
{
// 每次把数据装入桶子前先清空count
int count[10] = { 0 }; // 计数器 每次循环都清零
for (int j = 0; j < length; j++)
{
// 统计尾数为0-9的个数,一次是个十百千....位
int tail_number = (b[j] / radix) % 10;
count[tail_number]++; // 每个桶子里面的个数
}
// 桶中的每一个数的位置一次分配到temp数组中,先找到位置
for (int j = 1; j < 10; j++)
{
count[j] += count[j - 1];
}
// 分配到temp中排序后的位置
for (int j = length - 1; j >= 0; j--)
{
int tail_number = (b[j] / radix) % 10;
temp[count[tail_number] - 1] = b[j];
count[tail_number]--;
}
// 赋值
for (int j = 0; j < length; j++)
{
b[j] = temp[j];
}
radix *= 10;
} // for(int i)
delete[] temp;
}
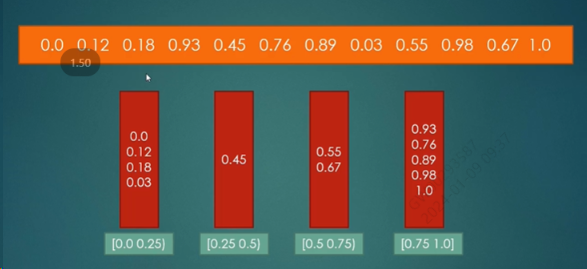
桶排序O(n+k)
**思路:**基数排序和计数排序都是桶思想的应用。桶排序是最基本的
首先要得到整个待排序数组的最大值和最小值,然后设置桶的个数k,这样可以得到每个桶可以放的数的区间。
然后遍历待排序的数组,将相关区间内的数放到对应的桶中,这样桶内在排序,就使得整个序列相对有序
图解:
代码:
void bucketSort(int arr[], int len)
{
// 确定最大值和最小值
int max = INT_MIN;
int min = INT_MAX;
for (int i = 0; i < len; i++)
{
if (arr[i] > max)
max = arr[i];
if (arr[i] < min)
min = arr[i];
}
// 生成桶数组
// 设置最小的值为索引0,每个桶间隔为1
int bucketLen = max - min + 1;
// 初始化桶
int bucket[bucketLen];
for (int i = 0; i < bucketLen; i++)
bucket[i] = 0;
// 放入桶中
int index = 0;
for (int i = 0; i < len; i++)
{
index = arr[i] - min;
bucket[index] += 1;
}
// 替换原序列
int start = 0;
for (int i = 0; i < bucketLen; i++)
{
for (int j = start; j < start + bucket[i]; j++)
{
arr[j] = min + i;
}
start += bucket[i];
}
}