前言
如果一个数组的左右区间都有序,我们可以使用一种方法(归并),使这个数组变得有序。
如下图:
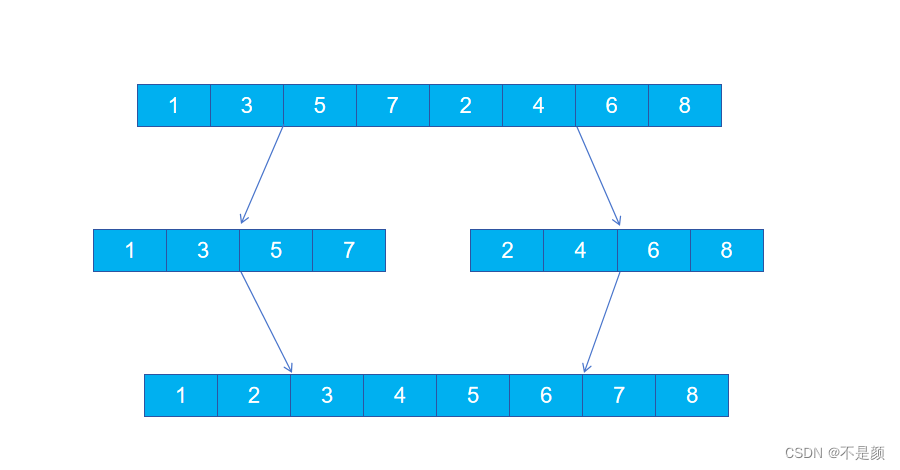
过程也很简单,分别取左右区间中的最小元素,再把其中较小的元素放到临时数组中,例如第一次1和2被取出,1 被放到临时数组;第二次3和2被取出,2 被放到临时数组。重复此操作就能得到有序的临时数组,最后把临时数组拷贝到原数组中就好了。
这就是归并的思想,目前先依照上面过程写出归并方法的代码。注意不是归并排序的代码
#include <iostream>
using namespace std;
void mergeAdd0(int arr[], int left, int right,int *temp) //函数参数传入临时数组
{
int mid = (left + right) / 2 ; //区间的中间位置,[left,mid]为左区间,[mid+1,right]为右区间
int i = left; //指向左区间最小元素的位置
int j = mid + 1 ; //指向右区间最小元素的位置
int k = 0; //临时数组的下标
while (i <= mid && j <= right) //这个循环是取出元素的过程
{
if (arr[i] < arr[j])
{
temp[k++] = arr[i++];
}
else
{
temp[k++] = arr[j++];
}
}
//因为有一个区间的元素必定会先被取完,下面两个循环是将另一个区间的元素拿到临时数组
while (i <= mid)
{
temp[k++] = arr[i++];
}
while (j <= right)
{
temp[k++] = arr[j++];
}
//将temp数组拷贝到原数组
memcpy(arr + left, temp, sizeof(int) * (right - left + 1 ));
}
int main(void)
{
int arr[] = { 1 , 3, 5 ,7 ,2 ,4 ,6 ,8 };
int len = sizeof(arr) / sizeof(arr[0]);
int* temp = new int[len]; //和原数组大小一样的临时数组
mergeAdd0(arr, 0, len - 1,temp);
for (int i = 0; i < len; i++)
{
cout << arr[i] << " ";
}
return 0;
}看完了归并方法,有些人会问,你这个归并方法并不能适用于一般情况,一般数组都是无序的,哪里是你那样的数组:左半边有序,右半边也有序。
也是,下面请先看看归并排序的过程吧(也就是处理一般情况)。
具体步骤
接下来讲的就是排序本身的具体步骤了,对于下面待排序的数组
——170 189 187 186 169 173 162 170 168——
先以中间为界,均分为A、B两组(如果是奇数个,允许两组的个数相差一个)
A——170 189 187 186 169——
B——173 162 170 168——
如果A、B两组数据有序的话,那么就可以通过上面的归并方法让数组有序,可是此时两个数组都无序,此时可以使用分治法继续对A、B两组进行均分,以B组为例,可以分为B1、B2组如下:
B1——173 162——
B2——170 168——
均分后依旧无序,继续利用分治法细分,以B1组为例,可分为如下两组
B11——173——
B12——162——
数组细分到一个元素后,这时候就可以使用之前的归并法借助一个临时数组将B1组有序化!B2数组同理。
B1——162 173——
B2——168 170——
依次类推,B1、B2组有序后,可归并成有序的B组,A组同理。
A——169 170 186 187 189——
B——162 168 170 173——
最后将A、B两组通过归并法合并得到了有序的数组。
——162 168 169 170 170 173 186 187 189——
思路
上面这个过程,按我的理解是:首先归并方法可以使一个左区间有序、右区间有序的数组有序,那左区间怎么有序呢?
恭喜你,学会抢答了。那就是左区间的左区间有序并且左区间的右区间有序(使用归并方法),右区间同理。那左区间的左区间如何有序呢?……直到细分到区间内只有一个元素时,可以保证这个区间有序,从而得到一个个有序区间,最终使数组有序。
这个过程正如排序的名称归并,先递归,使大问题变成小问题,再合并,依次解决问题。
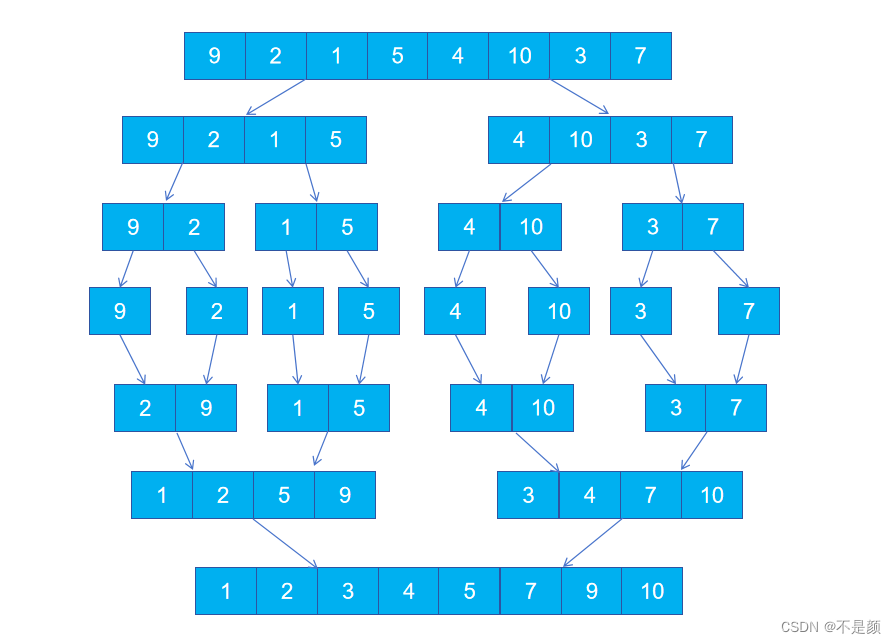
就如上过程结合归并方法可以得到以下代码:
//归并排序
void mergeSort(int arr[], int left, int right, int* temp)
{
if (left < right) //区间大于1个数,就要分而治之
{
int mid = (left + right) / 2;
mergeSort(arr, left, mid, temp);
mergeSort(arr, mid+1, right, temp);
mergeAdd(arr, left, right, temp);
}
}归并排序时间复杂度:n
全部代码以及测试图
#include <iostream>
#include <time.h>
using namespace std;
//归并方法
void mergeAdd(int arr[], int left, int right,int *temp)
{
int mid = (left + right) / 2 ; //区间的中间位置,[left,mid]为左区间,[mid+1,right]为右区间
int i = left; //指向左区间最小元素的位置
int j = mid + 1 ; //指向右区间最小元素的位置
int k = 0; //临时数组的下标
while (i <= mid && j <= right)
{
if (arr[i] < arr[j])
{
temp[k++] = arr[i++];
}
else
{
temp[k++] = arr[j++];
}
}
while (i <= mid)
{
temp[k++] = arr[i++];
}
while (j <= right)
{
temp[k++] = arr[j++];
}
//将temp数组拷贝到原数组
memcpy(arr + left, temp, sizeof(int) * (right - left + 1 ));
}
//归并排序
void mergeSort(int arr[], int left, int right, int* temp)
{
if (left < right) //区间大于1个数,就要分而治之
{
int mid = (left + right) / 2;
mergeSort(arr, left, mid, temp);
mergeSort(arr, mid+1, right, temp);
mergeAdd(arr, left, right, temp);
}
}
int main(void)
{
int arr[] = { 170 ,189,187 ,186 ,169 ,173 ,162 ,170 ,168 };
int len = sizeof(arr) / sizeof(arr[0]);
int* temp = new int[len]; //和原数组大小一样的临时数组
mergeSort(arr, 0, len - 1, temp);
for (int i = 0; i < len; i++)
{
cout << arr[i] << " ";
}
return 0;
}