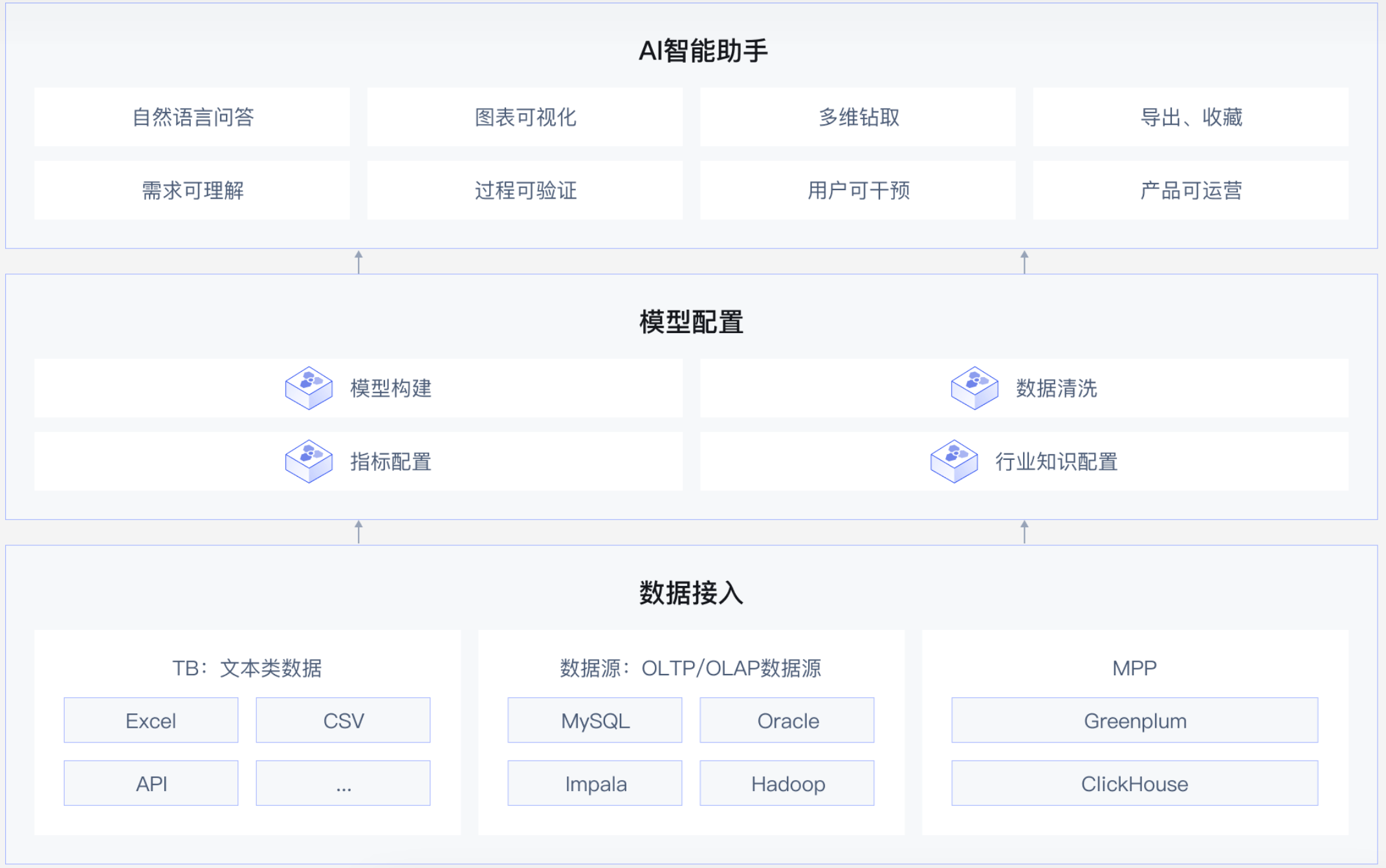
题目

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请

你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

示例 2：

输入：nums = [0,1,1]
输出：[]
解释：唯一可能的三元组和不为 0 。

示例 3：

输入：nums = [0,0,0]
输出：[[0,0,0]]
解释：唯一可能的三元组和为 0 。

提示：

• 3 <= nums.length <= 3000
• -10^5 <= nums[i] <= 10^5

思路 

本题与四数之和Ⅱ的区别在于，本题得到的结果需要去重，如果用哈希法，去重将会十分困难并且很难做到bug free，因此我们采用双指针法来进行简化的去重和结果的实现，详细的去重细节请看下面的代码所描述的，认真观察和思考去重，是本题的一大重点。

代码实现

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>>result;//用于存储结果
        int i,left,right;
        sort(nums.begin(),nums.end());
        //对数组进行排序，好处有两个
        //1.方便我们使用双指针不断移动，向中间靠拢 2.如果发现第一位是大于0的数那么就及时终止
        for(i=0;i<nums.size();i++){
            if(nums[i]>0)return result;//如果发现i也就是第一位大于0
                                       //后面加和也一定不可能等于0，故及时终止
            if(i>0&&nums[i]==nums[i-1])//对第一位进行去重，这里一定要是后一位和前一位相比
            //因为如果前一位和后一位相比的话会导致重复元素无法计数，后一位比前一位，这样可以
            //刚好越过重复元素，避免-1 -1 2情况
                continue;
            left=i+1;//设置初始第二个值，也就是双指针左端
            right=nums.size()-1;//设置初始第三个值，也就是双指针右端
            while(left<right){//因为如果双指针相等，那么就重复了同一个数字，不能让其相等
                if(nums[i]+nums[left]+nums[right]<0)left++;
                //如果和小于0，那么说明和过小，让左端向右移动，也就是变大
                else if(nums[i]+nums[left]+nums[right]>0)right--;
                //如果和大于0，那么说明和过大，让右端向左移动，也就是变小
                //这样做刚好可以遍历所有值
                else{
                    result.push_back(vector<int>{nums[i],nums[left],nums[right]});
                    //如果发现所需值，就让其插入结果集
                    while(left<right&&nums[left+1]==nums[left])left++;
                    //对第二个数进行去重，如果一直相等一直右移
                    while(left<right&&nums[right]==nums[right-1])right--;
                    //对第三个数进行去重，如果一直相等一直左移
               //如果该去重放在一开始，那么0 0 0 情况就会被省略，因此我们至少找到一组再去重
                    left++;
                    right--;
                    //找到一组就相对收缩一次，和前面的去重不矛盾，因为去重一直去的是相同值
                };
            }
        }
        return result;//返回结果集
    }
};

关键点：去重

①对第一个数去重

if(i>0&&nums[i]==nums[i-1])//对第一位进行去重，这里一定要是后一位和前一位相比
            //因为如果前一位和后一位相比的话会导致重复元素无法计数，后一位比前一位，这样可以
            //刚好越过重复元素，避免-1 -1 2情况
    continue;

②对第二个数去重

while(left<right&&nums[left+1]==nums[left])left++;
                    //对第二个数进行去重，如果一直相等一直右移

③对第三个数去重

 while(left<right&&nums[right]==nums[right-1])right--;
                    //对第三个数进行去重，如果一直相等一直左移

④去重位置和逻辑

1.对于第一个数的去重，我们要考虑是后一位和前一位相比进行去重，否则会导致，结果集缺失存在相同元素，类似于-1 -1 2的结果集。

2.对于第二第三个数的去重，我们要考虑的是去重的位置，如果过于提前，那么可能导致结果集缺失或者为空的结果集，类似于0 0 0的结果集。

总结

这道题简化了哈希算法，采用了双指针，虽然时间复杂度也不低，但是为我们提供了新的思路和思考，对bug free降低了要求，做好本题主要在于对关键点的把握和关注，如果把握好了去重的逻辑和位置，以及去重的细节和理解，那么相信做对这道题对你来说就是易如反掌。

尾声

本题通过复杂的去重和剪枝，告诉我们哈希算法的不利情况和相应的代替算法，希望大家通过本题对双指针和哈希表的认识和理解进一步加深，如果觉得笔者写的还不错的话，记得留下您的点赞，关注和收藏，和作者一起学习算法呀~