文章目录
- 📑前言
- 一、for循环基础
- 1.1 语法
- 1.2 示例
- 1.3 流程图
- 1.4 for与while的对比
- 二、for循环进阶
- 2.1 for中的break和continue
- 2.2 for语句的循环控制变量
- 2.3 for循环变种
- 2.4 笔试巩固题
- 🌤️全篇总结

📑前言
在C语言中,for循环是一种常用的循环结构,具有灵活的语法和强大的功能。本文将深入探讨for循环的基础语法、进阶用法以及注意事项,以帮助读者更好地理解和运用for循环。
一、for循环基础
1.1 语法
for(表达式1; 表达式2; 表达式3)
循环语句;
表达式1
表达式1为初始化部分,用于初始化循环变量的。
表达式2
表达式2为条件判断部分,用于判断循环时候终止。
表达式3
表达式3为调整部分,用于循环条件的调整。
1.2 示例
在了解了基础的语法后,我们来看一段示例的代码,让你对for循环有深的理解。
int main()
{
int i = 0;
//for(i=1/*初始化*/; i<=10/*判断部分*/; i++/*调整部分*/)
for(i=1; i<=10; i++)
{
printf("%d ", i);
}
return 0;
}
1.3 流程图
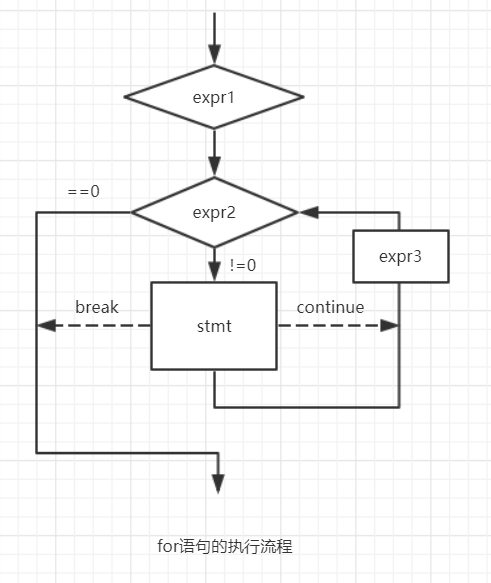
1.4 for与while的对比
int i = 0;
//实现相同的功能,使用while
i=1;//初始化部分
while(i<=10)//判断部分
{
printf("hehe\n");
i = i+1;//调整部分
}
//实现相同的功能,使用for
for(i=1; i<=10; i++)
{
printf("hehe\n");
}
可以发现在while循环中依然存在循环的三个必须条件,但是由于风格的问题使得三个部分很可能偏离较远,这样
查找修改就不够集中和方便。所以,for循环的风格更胜一筹;for循环使用的频率也最高。
二、for循环进阶
2.1 for中的break和continue
for循环中也可以出现break和continue,他们的意义和在while循环中是一样的。
但是还是有些差异:
//代码1
#include <stdio.h>
int main()
{
int i = 0;
for(i=1; i<=10; i++)
{
if(i == 5)
break;
printf("%d ",i);
}
return 0;
}
//代码2
#include <stdio.h>
int main()
{
int i = 0;
for(i=1; i<=10; i++)
{
if(i == 5)
continue;
printf("%d ",i);
}
return 0;
}
在代码1中,当i等于5时,使用break语句会使循环立即终止,不再执行剩下的循环体,输出结果为1 2 3 4。
而在代码2中,当i等于5时,使用continue语句会跳过当前循环,继续下一次循环,输出结果为1 2 3 4 6 7 8 9 10。
因此,break语句会完全终止循环,而continue语句只是跳过当前循环,继续下一次循环。
2.2 for语句的循环控制变量
建议:
- 不可在for 循环体内修改循环变量,防止 for 循环失去控制。
- 建议for语句的循环控制变量的取值采用“前闭后开区间”写法
int i = 0;
//前闭后开的写法
for(i=0; i<10; i++)
{}
//两边都是闭区间
for(i=0; i<=9; i++)
{}
2.3 for循环变种
for循环中的初始化部分,判断部分,调整部分是可以省略的。
- 初始化部分省略:循环中无法初始化循环变量,可能导致循环变量未被正确初始化而造成意外行为。
- 判断部分省略:循环条件无法被判断,导致无法退出循环,造成无限循环。
- 调整部分省略:循环中无法对循环变量进行调整,可能导致循环变量无法按预期进行调整而造成意外行为。
因此,虽然 for 循环中的初始化部分、判断部分、调整部分是可以省略的,但是不建议全部省略,否则可能会导致程序无法正常工作或者产生意外行为。
for(;;)
{
printf("hehe\n");
}
for循环的嵌套
for(int i=0; i<10; i++)
{
for(int j=0; j<10; j++)
{
printf("hehe\n");
}
}
多变量控制循环
int x, y;
for (x = 0, y = 0; x<2 && y<5; ++x, y++)
{
printf("hehe\n");
}
2.4 笔试巩固题
请问下面代码循环要循环多少次?
#include <stdio.h>
int main()
{
int i = 0;
int k = 0;
for(i =0,k=0; k=0; i++,k++)
k++;
return 0;
}
这段代码的问题在于for循环的条件部分。
在C语言中,= 是赋值操作符,而 == 才是比较操作符。
在这段代码中,for(i =0,k=0; k=0; i++,k++) 中的 k=0 是一个赋值操作,而不是比较操作。这意味着这个条件永远为真,导致无限循环。
所以,这段代码的问题是无限循环,因为 for 循环的条件永远为真。
🌤️全篇总结
看到这里相信聪明的你已经对for循环的基础语法有了深入的了解,并且掌握了for循环的进阶用法和注意事项。for循环作为一种强大的循环结构,可以帮助程序实现复杂的逻辑控制和重复执行任务。在实际编程中,合理灵活地运用for循环,可以提高代码的效率和可读性,为程序的开发和维护带来便利。