今年早些时候,我为 MAKE 杂志写了一篇教程,介绍如何制作视频游戏角色的毛绒动物。 该技术采用给定的角色 3D 模型及其纹理,并以编程方式生成缝纫图案。 虽然我已经编写了一般摘要并将源代码上传到 GitHub,但我在这里编写了对使这一切成为可能的数学的更深入的解释。
NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎
我的项目目标是创建一个可打印的缝纫图案,一旦缝合在一起,就会接近起始 3D 模型(在本例中为视频游戏角色)。 我的技术要点是使用 3D 模型的纹理图像文件作为缝纫图案。 纹理图像应该能够在其 UV 接缝处连接以重建原始 3D 形状。 3D 模型的初始纹理图像可能未针对缝合重建进行优化,但可以通过从原始模型创建一组新的 UV(接缝针对缝合进行了更优化)来进行补救。 给定原始 UV 和新 UV,可以为每个面计算变换矩阵,以将旧纹理图像变换为新的优化纹理图像。 缝合重建的分辨率取决于接缝的位置和 UV 展开算法的变形量。
如一般摘要中所述,3D 模型由几个不同的特征组成。 它具有定义其 3D 形状的顶点、边和面。 它还具有一组 UV 坐标,用于定义纹理如何投影到每个面上。 最后,它具有定义 3D 模型着色方式的纹理图像。

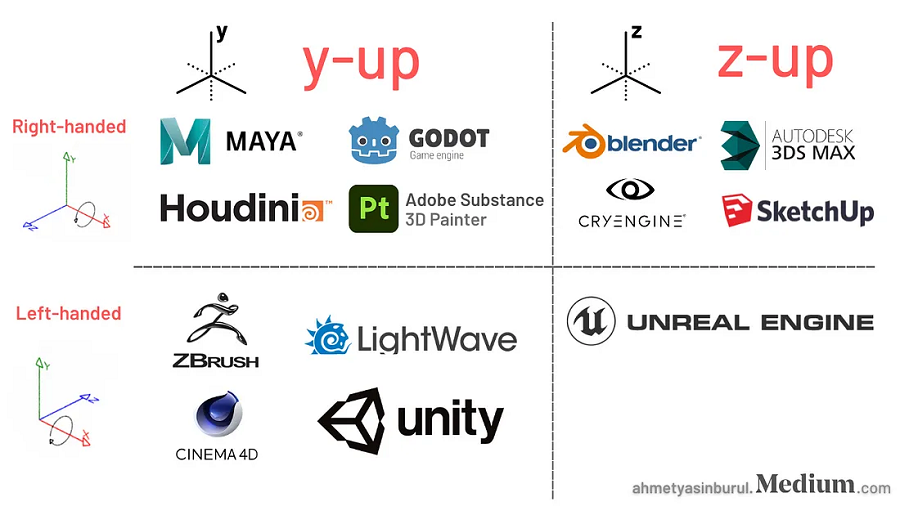
UV 映射是将 3D 面投影到 2D 纹理表面的过程,在计算机图形学领域得到了很好的研究。 3D 模型的每个面都映射到 UV 贴图上的一个面。 UV贴图上的每个面对应3D模型上的一个面,UV保留了3D模型的面之间的边缘关系。 筑波大学的 Yuki Igarashi 博士意识到了 UV 的这一特性,并在她的论文 Plushie: An Interactive Design System for Plush Toys (SIGGRAPH 2006) 和Pillow: Interactive Flattening of a 3D Model for Plush Toy Design(SIGGRAPH 2007) 中使用 UV 从动态创建的 3D 模型中创建缝纫图案。 她的UV贴图的具体算法是ABF++。
由于 UV 贴图可以用作缝纫图案,因此纹理图像也可以,因为 UV 将纹理图像映射到 3D 模型上。 纹理可以打印到织物上,并且根据图案缝制而成的毛绒动物将保留原始 3D 模型的颜色信息。
然而,并非每个 UV 贴图都针对缝纫图案创建进行了优化。 正如你在上面看到的,UV 相互折叠,因此 UV 和主体减半。 这是视频游戏图形中一种流行的节省空间的技术。 头部也比身体大得多,因此在视频游戏中头部会显得有更精细的细节。 这些优化不适合缝纫图案,因为我们希望身体在 3D 空间中的比例与 2D UV 空间中的比例大致相同。

最终分辨率的差异, 来自Igarashi
UV 簇的接缝将成为最终毛绒动物上的接缝。 从相同的 3D 模型开始,接缝位置将决定最终缝制作品的分辨率。
我的模型的初始 UV 不适合毛绒动物创作,因此我制作了自己的 UV,以优化它们以进行缝纫。 大多数现代 3D 图形软件都具有 UV 映射功能(Maya、Blender、3ds Max 等)。 在我的项目中,我使用了 UVLayout,这是一种专门的 UV 映射工具,但正如 MAKE 杂志文章中所见,Blender 也能正常工作。
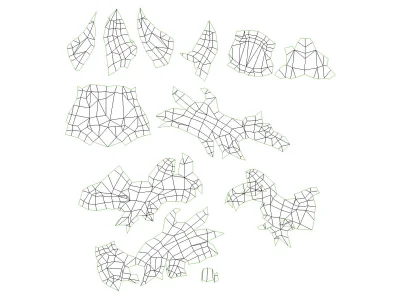
我最终的 UV 贴图的一部分
有了新创建的 UV 贴图,我想创建一个与其相对应的新纹理贴图,并将其打印为我的最终缝纫图案。 这就是线性代数派上用场的地方。
UV 贴图上的多边形面被分解为三角形。 旧的原始 UV 上的每个三角形面通过它们与 3D 模型上同一面的关系映射到新 UV 上的三角形。 由于两个三角形代表相同的形状,但在 UV 贴图上具有不同的坐标,因此可以计算两个三角形之间的变换矩阵。 使用三角形是因为我们想要使用方阵进行计算。 该变换矩阵可用于变换旧纹理上的相应三角形区域,以对新纹理上的新三角形区域进行着色。 Stackoverflow 对如何根据两个三角形的坐标计算变换矩阵以及我使用的有用代码片段进行了很好的解释。
如果计算每个 UV 三角形的变换矩阵并变换其相应的纹理三角形,最终结果将是一个新的纹理。 如果将新纹理和新 UV 应用到原始 3D 模型,其视觉外观应该不会有任何差异。
在我的实现中,首先将 UV 坐标映射到纹理图像上的像素坐标,然后计算变换矩阵。 映射(与浮点不精确相结合)导致了一些舍入问题(因为像素坐标必须是整数),这在求解变换矩阵期间导致了奇异矩阵。 我的黑客解决方案是将 UV 点之一的像素坐标之一偏移 1 个像素。 我认为最终打印图案上的 1 个像素不太明显。
例如:
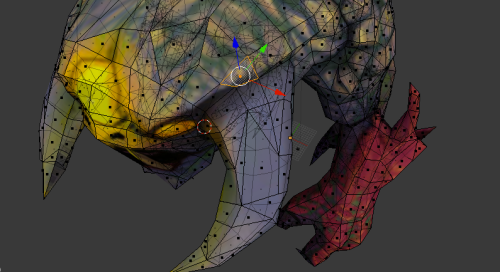
上面是 3D 模型,突出显示的脸部是感兴趣的脸部。

对应于原始 UV 贴图上的面,其 UV 坐标为 (0.7153, -0.2275)、(0.78, -0.1982)、(0.7519, -0.0935)、(0.7207, -0.0382)。

正如你所看到的,UV 将纹理图像映射到 3D 模型。

该特定的 UV 面控制纹理图像上的一小部分。

3D 模型上突出显示的面也对应于我创建的新 UV 贴图上的面。
其坐标为 (0.046143, 0.63782)、(0.133411, 0.683826)、(0.09056, 0.660572)、(0.108221, 0.6849)。
给定两组 UV 坐标,我将 UV 四边形分解为两个三角形并计算变换矩阵。
为了计算变换矩阵,建立方程如下:
![]()
其中 W 是包含新 UV 坐标的矩阵,A 是变换矩阵,Z 是包含旧 UV 坐标的矩阵。
由于使用齐次坐标,W和Z是3×3方阵,最后一行为[1 1 1],A也是3×3方阵,最后一行为[0 0 1]。有关更多详细信息,请参阅仿射变换。
用实际坐标填充我们的矩阵给出以下两个方程。 原始 UV 坐标映射到像素坐标 (384, 72)、(396, 80)、(401, 67)、(383, 61)。 新的 UV 坐标映射到 (29, 174)、(23, 185)、(33, 188)、(35, 172)。 我使用像素坐标进行转换。

如前所述,有两个方程,因为我将四边形分成两个三角形。
为了求解 A,我可以取 Z 的倒数并将其乘以 W。由于 Z 是方阵,因此 Z 是可逆的,因为它的行列式不为零。 Z 的行列式不为零,因为行列式表示它所包围的三角形的面积。
![]()
![]()
然而,在实际实现中,我以更直接的方式解决了这个问题,即进行A和Z之间的矩阵乘法并求解未知数系统。 在这里相关信息。
当应用于原始 UV 控制的纹理图像区域时,我得到以下转换后的纹理图像片段:

转换每个纹理图像区域后,你将获得以下可以打印的纹理图像。橙色箭头表示变换后的纹理块适合整个纹理图像的位置。

这就是如何从 3D 模型创建缝纫图案的更理论/数学解释。
原文链接:3D展2D数学原理 - BimAnt