- 自己在学习过程中总结了DS中几乎所有的应用题,可以用于速通期末考/考研/各种考试。
- 很多方法来源于B站大佬,底层原理本文不做过多介绍,建议自己研究。
- 例题大部分选自紫皮严书。
- pdf版在主页资源
一、递归时间/空间分析
1.时间复杂度的分析
设
F
a
c
t
(
n
)
Fact(n)
Fact(n)的执行时间是
T
(
n
)
T(n)
T(n)。
if(n==0) return 1; 的执行时间是
O
(
1
)
O(1)
O(1),
F
a
c
t
(
n
−
1
)
Fact(n-1)
Fact(n−1)的执行时间是
T
(
n
−
1
)
T(n-1)
T(n−1),
所以else return
n
∗
F
a
c
t
(
n
−
1
)
n*Fact(n-1)
n∗Fact(n−1); 的执行时间是
O
(
1
)
+
T
(
n
−
1
)
O(1)+T(n-1)
O(1)+T(n−1)。
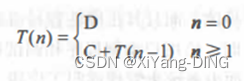
推出: T ( n ) = n C + T ( 0 ) = n C + D T(n)=nC+T(0)=nC+D T(n)=nC+T(0)=nC+D, T ( n ) = O ( n ) T(n)=O(n) T(n)=O(n)
【小结论】:Fibonacci数列和Hanoi塔问题递归算法的时间复杂度均为O(2^n)。
2.空间复杂度分析
空间复杂度 S ( n ) = O ( f ( n ) ) S(n)=O(f(n)) S(n)=O(f(n)),其中, f ( n ) f(n) f(n)为“递归工作栈”中工作记录的个数与问题规模 n n n 的函数关系。
【小结论】:阶乘间题、Fibonacci数列问题、Hanoi塔问题的递归算法的空间复杂度均为O(n)。
二、KMP算法求next数组和nextval
1.next[i]
前2位一般为:0,1
i位看前i-1位最大公共部分末尾坐标+1
2.nexval[i]
前1位一般为:0
t[next[i]]位置元素是不是和t[i]一样,一样的话将t[next[i]]的nextval写在当前nextval[i];不一样的话就将当前的next[i]里面数写在nextval[i]
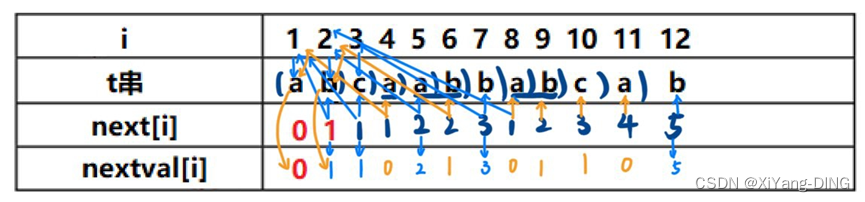
例题1已知模式串t=“abcaabbabcab”, 写出用KMP法求得的每个字符对应的next和nextval函数值。
例题2、3
三、数组存贮(选择&简答)
1.对称矩阵
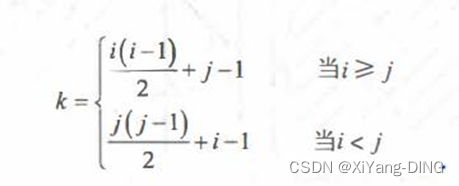
2.三角矩阵
(1)上三角
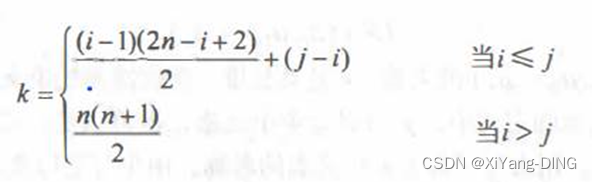
(2)下三角

例题1假设以行序为主序存储二维数组 A = array[ 1…100, 1…100] , 设每个数据元素占2个存储单元,基地址为10, 则 LOC[5,5] = ( )。
【解析】LOC[5,5]有(5-1)满行,最后一行有(5-1)个
Loc[5,5]=(4*100+4)*2+10=818
例题2数组A中,每个元素A[i,j]的长度均为32个二进制位,行下标从-1~9, 列下标从1 ~11,从首地址S开始连续存放在主存储器中,主存储器字长为16位。
求:
(1)存放该数组所需多少单元?
32/16=2字
11 * 11 * 2=242
(2)存放数组第4列所有元素至少需多少单元?
11*2=22
(3)数组按行存放时,元素A[7,4]的起始地址是多少?
【解析】A[7,4]有(7-1+2)满行,最后一行有(4)个
S+((6+2)*11+4-1)*2=S+182
(4)数组按列存放时,元素 A[4, 7]的起始地址是多少?
【解析】A[4, 7]有6满列,最后一列有(4+2)个
S+((7-1)*11+(4+2)-1)*2=S+142
例题3设有一个 10 阶的对称矩阵 A , 采用压缩存储方式以行序为主存储,a11为第一元素, 其存储地址为1,每个元素占一个地址空间,则a85的地址为( )。
(易错)若对n阶对称矩阵A以行序为主序方式将其下三角形的元素(包括主对角线上所有元素)依次存放于一维数组 B[1…(n (n+1))/2]中,则在B中确定aij (i<j)的位置k的关系为()
本来是i (i -1)/2 + j,但是(i<j) 所以j(j-1)/2+i
四、广义表—求表头/表尾/长度/深度(选择&简答)
1.取表头Head(A)
就取A的第一个元素
2.取表尾Tail(A)
就是扣掉第一个元素,留下的所有的(包含A最外面的大括号)
3.长度
就是元素的个数
//严书例子
(1) A = ()—A 是一个空表, 其长度为零。
(2) B=(e)—B 只有一个原子 e, 其长度为1。
(3) C= (a, (b, c, d))—C的长度为2, 两个元素分别为原子 a 和子表(b,c, d)。
(4) D = (A, B, C)—D 的长度为3,3个元素都是广义表。显然,将子表的值代入后,则有 D = ((), (e), (a, (b, c, d)))。
(5) E = (a, E)—这是一个递归的表,其长度为2。E 相当千一个无限的广义表 E=(a, (a, (a, ···)))。
4.深度
就是数左or右括号的个数
例题1设广义表 L = ((a,b,c)), 则 L 的长度和深度分别为( )
长度就是元素个数=1
深度就是数括号个数=2
例题2广义表((a,b,c,d))的表头是( ),表尾是( )
取表头Head(A)就取A的第一个元素=(a,b,c,d)
取表尾Tail(A)就是扣掉第一个元素,留下的所有的(包含A最外面的大括号)=( )
例题3广义表 A= (a,b,(c,d),(e,(f,g))), 则 Head(Tail(Head(Tail(Tail(A)))))的值为( )。
Tail(A)= (b,(c,d),(e,(f,g)))
Tail(Tail(A))= ( (c,d),(e,(f,g)))
Head(Tail(Tail(A)))= (c,d)
Tail(Head(Tail(Tail(A))))= (d)
Head(Tail(Head(Tail(Tail(A)))))=d
例题4请将香蕉 banana 用工具H( )—Head( ), T()—Tail( )从L中取出。
L = (apple, (orange, (strawberry, (banana)), peach), pear)
五、前/中/后/层序遍历二叉树+先后根遍历森林
1.前序/前缀表达式/波兰式
树:根左右
森林:根左到右
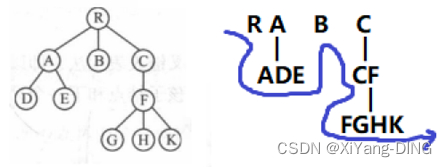
RADEBCFGHK
2.中序/中缀表示
树:左根右
把一个树拍扁了就是中序~
3.后序/后缀表达式/逆波兰式
树:左右根
森林:左到右根
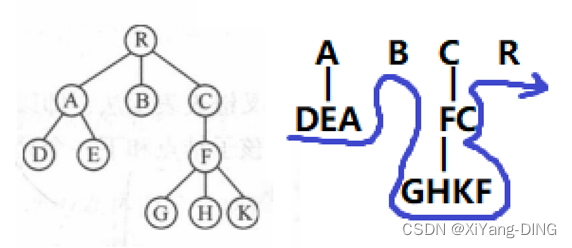
DEABGHKFCR
例题1试找出满足下列条件的二叉树
①先序序列与后序序列相同
【解析】根左右,左右根(不能删根!)
空树,只有根。
②中序序列与后序序列相同。
【解析】:左根右,左右根,根左右(不能删根!)
空树,只有左子树
③先序序列与中序序列相同。
【解析】:根左右,左根右(不能删根!)
空树,只有右子树
④中序序列与层次遍历序列相同。
【解析】:左根右,层序先输出根(不能删根!)
空树,只有右子树
六、前/后/层次+中序确定二叉树
1.前序+中序
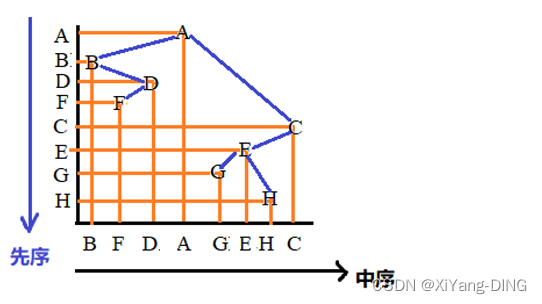
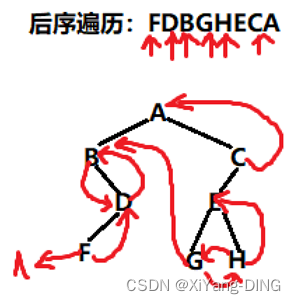
例题1设一棵二叉树的先序序列:ABDFCEGH,中序序列:BFDAGEHC。
①画出这棵二叉树。
②画出这棵二叉树的后序线索树。(后面)
③将这棵二叉树转换成对应的树(或森林)。(后面)
2.后序+中序
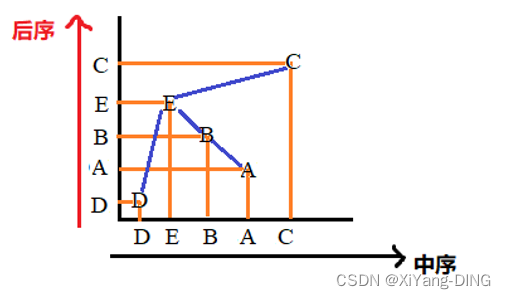
例题2已知后序序列:DABEC,中序序列:DEBAC,求二叉树
3.层次+中序
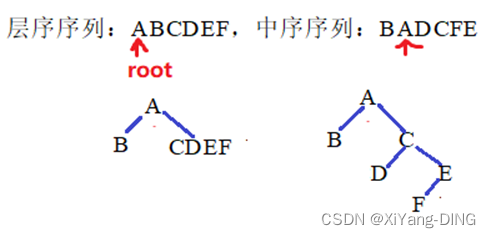
例题3已知层序序列:ABCDEF,中序序列:BADCFE,求二叉树
4.拓展
①已知前序有多少种二叉树?
入栈出栈个数:
1
/
(
n
+
1
)
C
2
n
n
1/(n+1) C_2n^n
1/(n+1)C2nn种(n为结点个数)
七、前中后序线索二叉树的构建
1.线索二叉树构建方法
Step1:写出对应的先/中/后序遍历
Step2:如果结点左孩子为空,结点左链连接序列左边的元素;如果结点右孩子为空,结点右链连接序列右边的元素;
例题1设一棵二叉树的先序序列:ABDFCEGH,中序序列:BFDAGEHC。
①画出这棵二叉树。
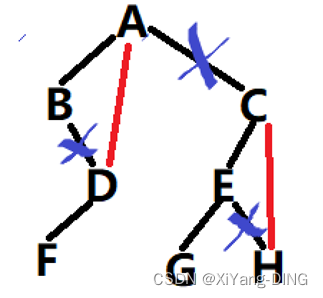
②画出这棵二叉树的后序线索树。
③将这棵二叉树转换成对应的树(或森林)。(后面)
八、树/森林与二叉树的转换
变森林/树:删右腿
变二叉树:连右兄弟
1.树→二叉树
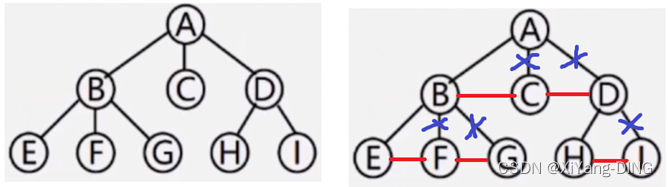
2. 二叉树→树
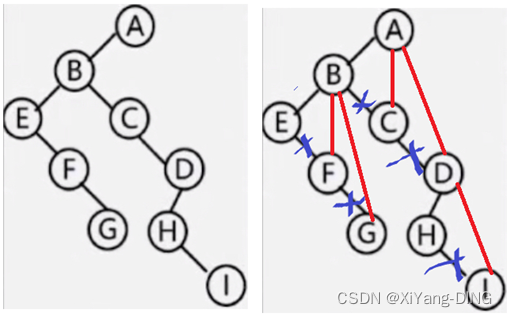
3.森林转→二叉树
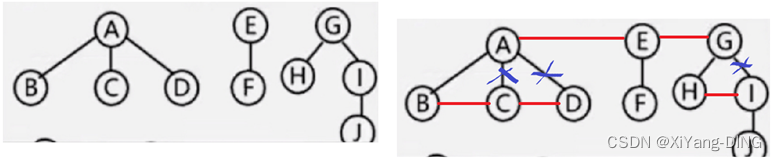
4.二叉树→森林
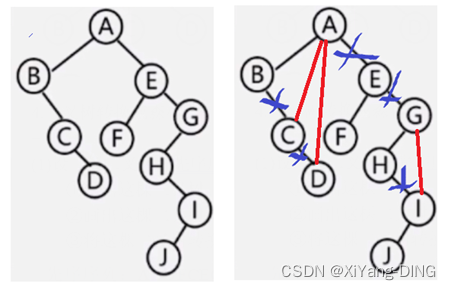
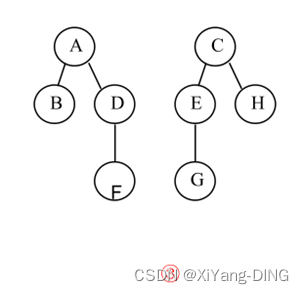
例题1设一棵二叉树的先序序列:ABDFCEGH,中序序列:BFDAGEHC。
①画出这棵二叉树。
②画出这棵二叉树的后序线索树。
③将这棵二叉树转换成对应的树(或森林)。
九、哈夫曼树——构造/WPL/HT初始和终结状态
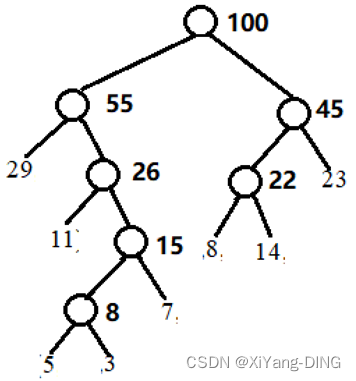
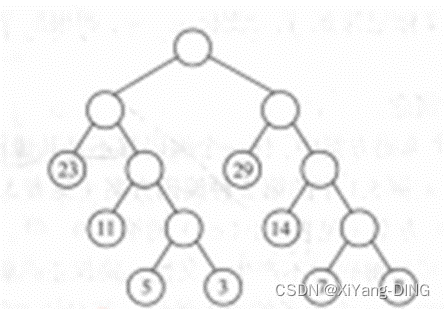
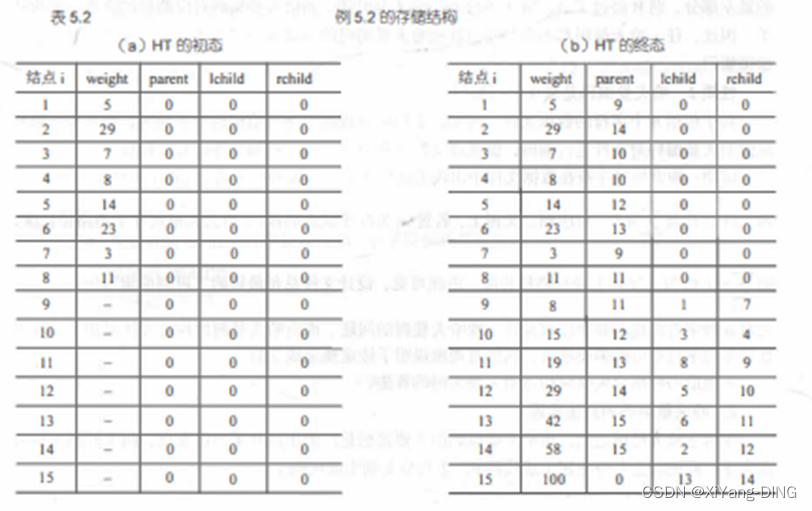
例题1已知w = (5,29,7,8,14,23,3,11), 构造一棵哈夫曼树,计算树的带权路径长度,并给出其构造过程中存储结构HT的初始状态和终结状态。
①哈夫曼树:
或
②WPL=292+113+74+55+35+83+143+232= 271
③
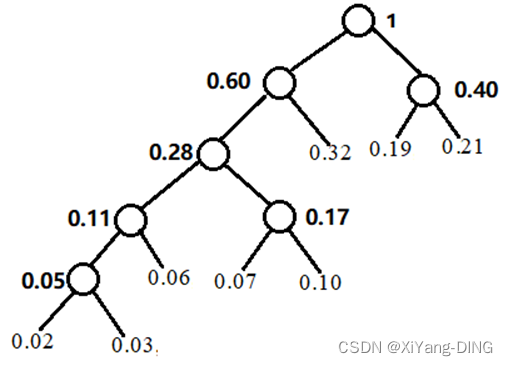
例题2假设用于通信的电文仅由8个字母组成,字母在电文中出现的频率分别为0.07, 0.19, 0.02, 0.06, 0.32, 0.03, 0.21 , 0.10。
①试为这8个字母设计哈夫曼编码。
②试设计另一种由二进制表示的等长编码方案。
等长编码需要3位2进制
③对于上述实例,比较两种方案的优缺点。
哈夫曼WPL=2*(0.19+0.21+0.32)+4*(0.07+0.10+0.06)+5*(0.02+0.03)=2.61(平均码长)
等长WPL=3*(0.19+0.32+0.21+0.07+0.06+0.10+0.02+0.03)=3(平均码长)
十、邻接矩阵/邻接表/逆邻接表/十字链表—构建、出入度
1.邻接矩阵
①无向图
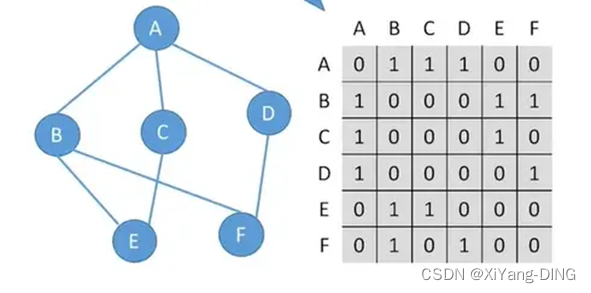
出入度:第i行or第j列非零元素的个数是顶点i的度
②有向图
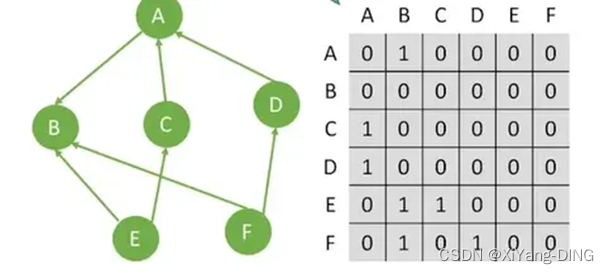
出入度:第i行非零元素的个数是顶点i的出度;第j列非零元素的个数正好是顶点i的入度
2.邻接表
①无向图

info是权重
出入度:遍历“一行”
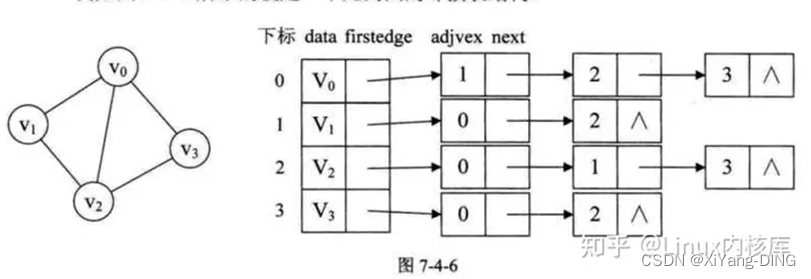
②有向图

出度:遍历“一行”
入度:遍历v的每行
3.逆邻接表
与邻接表箭头相反
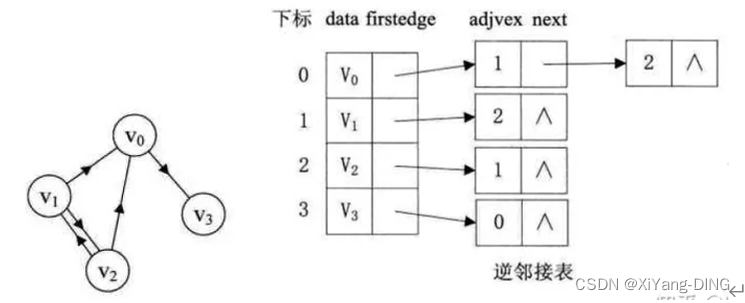
4.十字链表

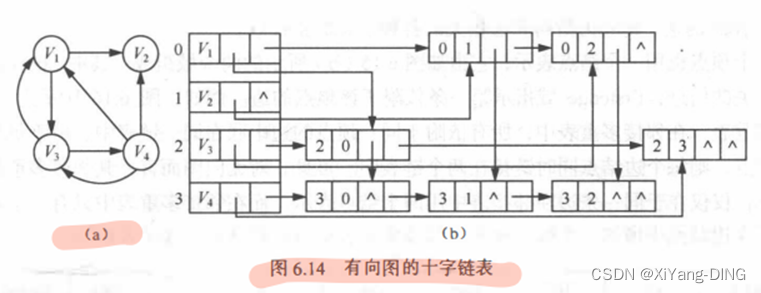
十字链表的画法
Step1.编号
Step2.组队:编号结点出去的箭头
Step3.连线:前同横线,后同竖线
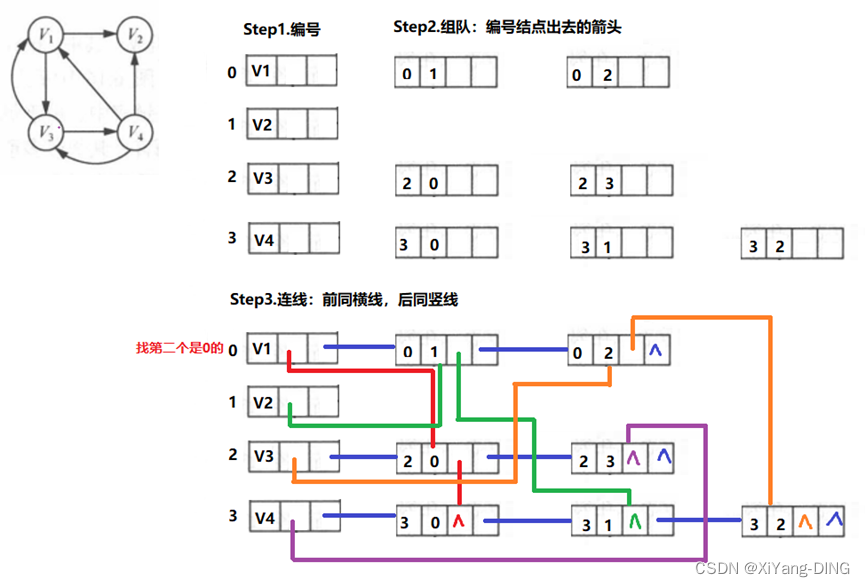
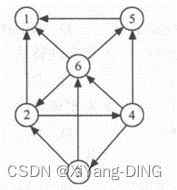
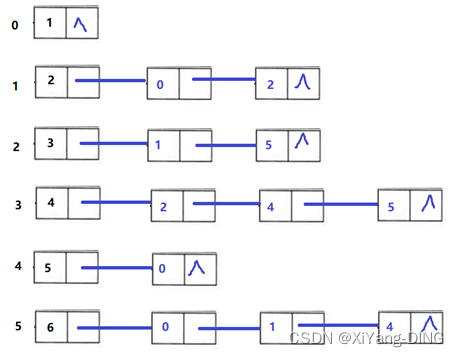
例题1已知有向图,请给出:
①每个顶点的入度和出度;
1的出:0;入:3
2的出:2;入:2
3的出:2;入:1
4的出:3;入:1
5的出:1;入:2
6的出:3;入:2
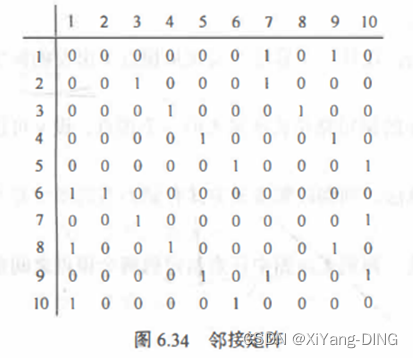
②邻接矩阵;
1 2 3 4 5 6
1 0 0 0 0 0 0
2 1 0 0 1 0 0
3 0 1 0 0 0 1
4 0 0 1 0 1 1
5 1 0 0 0 0 0
6 1 1 0 0 1 0
③邻接表;
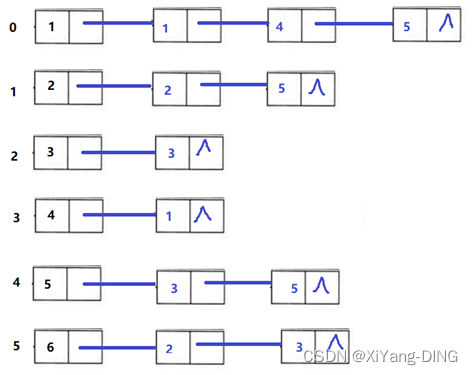
④逆邻接表。
例题2已知无向网,请给出:
①邻接矩阵;
②邻接表;
③最小生成树。(后面)
十一、生成树—深度优先/广度优先
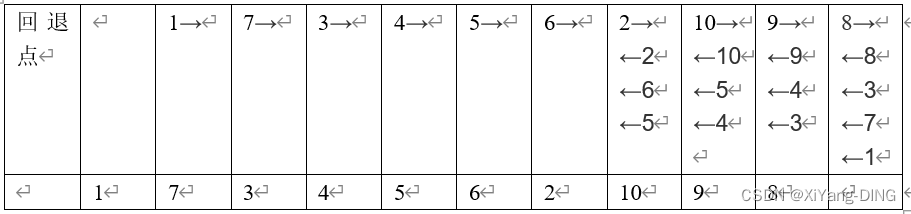
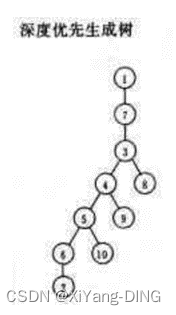
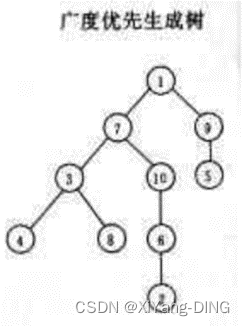
已知图的邻接矩阵。试分别画出自顶点1出发进行遍历所得的深度优先生成树和广度优先生成树。
深度优先
广度优先
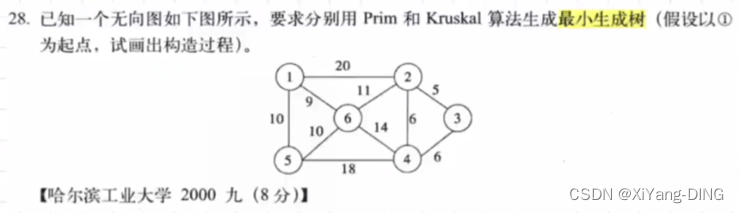
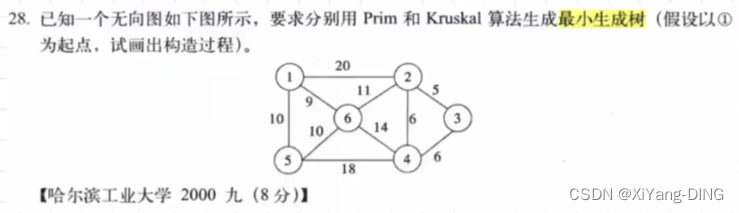
十二、最小生成树—Prim/Kruskal
1.普里姆 (Prim) 算法
从某点出发,找最短的边加入集合,再以集合为整体继续加入边。过程中不能出现回路!
例题1
1→6→5→2→3→4(不唯一)
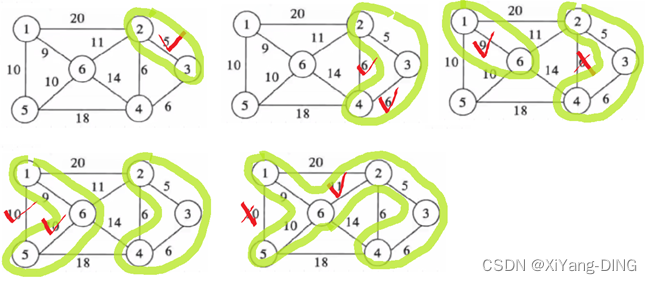
2.克鲁斯卡尔 (Kruskal) 算法
直接找最小的边,过程中不能出现回路!
例题1
例题2
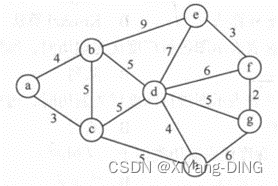
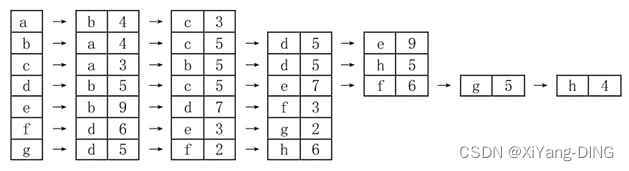
已知无向网,请给出:
②邻接表;
③最小生成树。
③Kruskal
十三、最短路径—Dijkstra/Floyd
1.从某个源点到其余各顶点的最短路径迪杰斯特拉(Dijkstra)算法
从某点出发,找最短的边加入集合,再以集合为整体继续加入边。
与Prim不同的是,Prim只用看集合相连的最短,Dijkstra还要算一算。
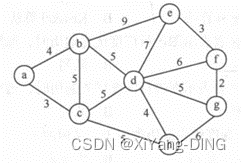
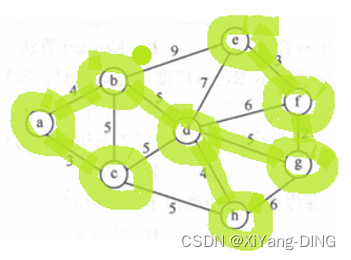
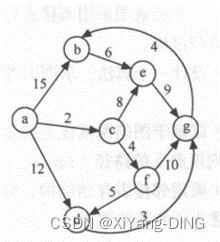
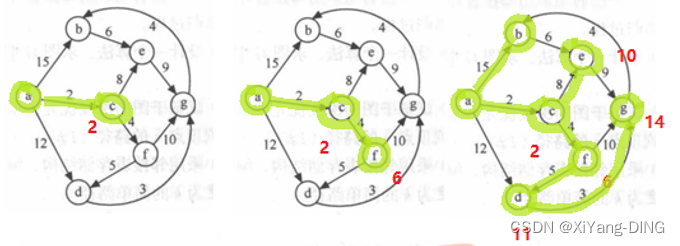
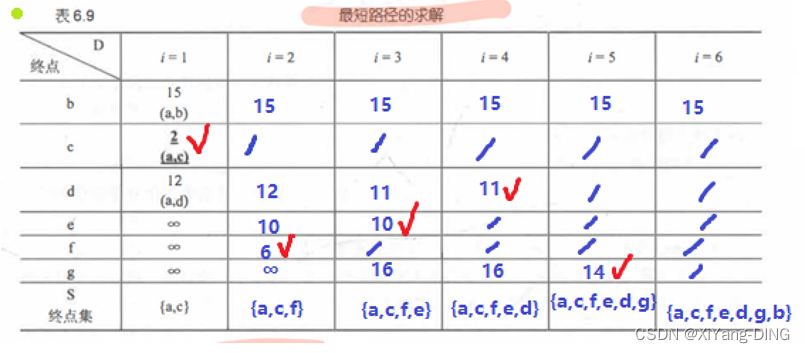
例题1试用迪杰斯特拉算法求出从顶点a到其他各顶点间的最短路径
2.每一对顶点之间的最短路径弗洛伊德(Floyd)算法
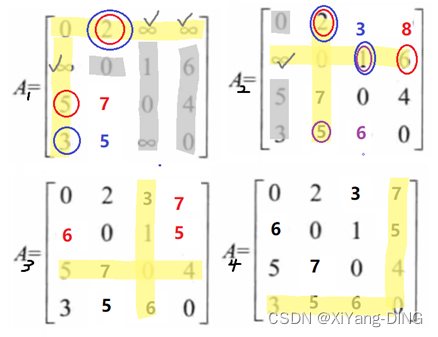
不断基于对角线上元素画“十字”计算的过程
Step1.从第一个对角线元素开始不断画十字
Step2.十字和它∞部分对应的行列值不变
Step3.更新值(值比原来元素小才更新)与路径,取下一个对角线元素继续重复
对于更新路径:A1中[5,2]从∞(5_31→2_12)更新为7(5→1→2)
十四、拓扑排序/逆拓扑排序
1.AOV-网
这种用顶点表示活动,用弧表示活动间的优先关系的有向图称为顶点表示活动的网。AOV-网是无环的有向图(DAG)
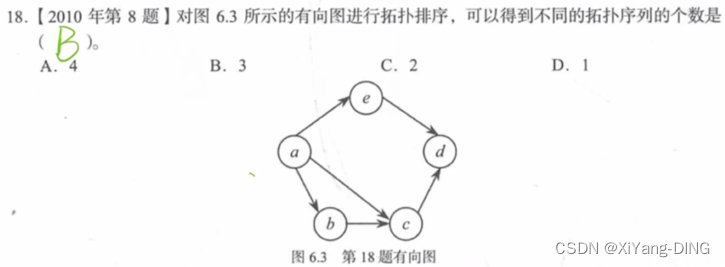
2. 拓扑排序
就是将AOV-网中所有顶点排成一个线性序列,该序列满足:若在AOV-网中由顶点Vi到顶点Vj有一条路径,则在该线性序列中的顶点Vi必定在顶点Vj之前。
拓扑排序做法
Step1.在有向图中选一个无前驱的顶点且输出它。
Step2.从图中删除该顶点和所有以它为尾的弧。
Step3.重复1.和2.直至不存在无前驱的顶点。
若此时输出的顶点数小于有向图中的顶点数,则说明有向图中存在环,否则输出的顶点序列即为一个拓扑序列。
逆拓扑排序做法
在有向图中选一个无后继的顶点且输出它。(其余和拓扑排序一样)
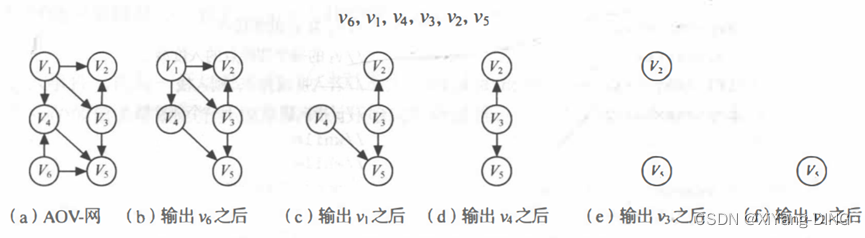
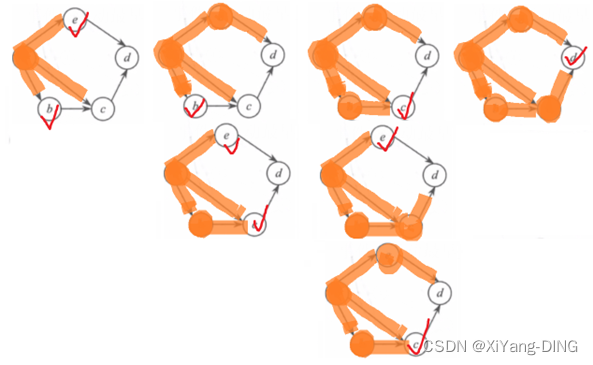
例题1
十五、AOE-网—事件&活动最早/最迟/时间余量/关键活动/关键路径
1. AOE-网
AOE-网是一个带权的有向无环图,其中,顶点表示事件,弧表示活动,权表示活动持续的时间
ve(1):事件v_1的最早发生时间
vl(1):事件v_1的最迟发生时间
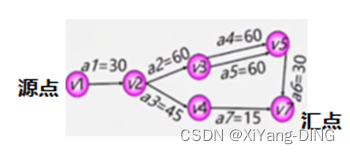
早顺迟逆;早+迟-;早大迟小
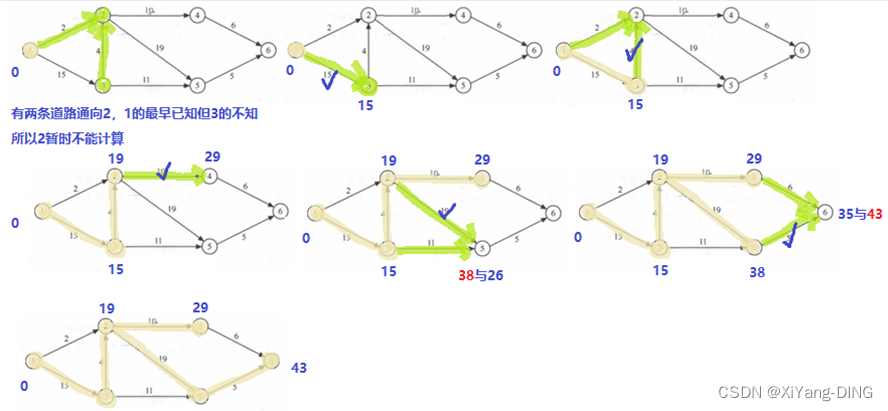
说明:最早时间从源点顺着往汇点走
最迟时间从汇点逆着往源点走
最早时间顺着走的时候遇到两条道路选相加最大的
最迟时间逆着走的时候遇到两条道路选相减最小的
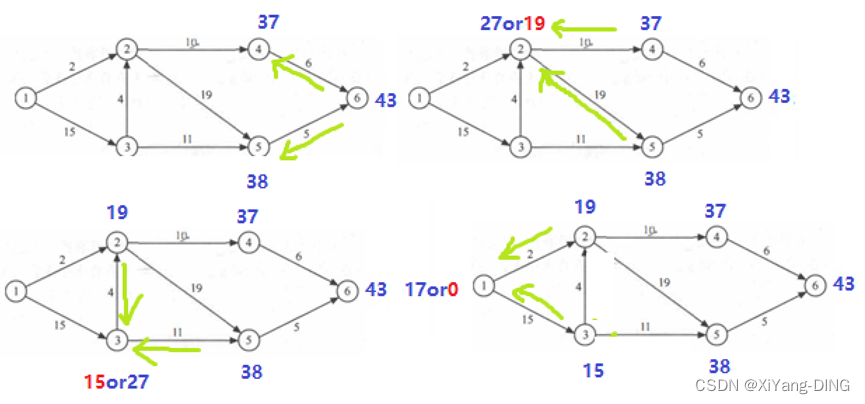
e(1):活动a_1的最早开始时间
l(1): 活动a_1的最迟开始时间
早=弧尾早;迟=弧头迟-权值
说明:最早时间是<x,y>弧尾事件的最早开始时间
最迟时间是<x,y>弧头事件的最迟开始时间-<x,y>的权值
2.关键路径
关键路径上的活动没有时间余量,即l(1)-e(1)=0
关键路径:路径长度最长的路径,完成工程至少需要的时间
关键路径上的活动是影响工程的关键活动
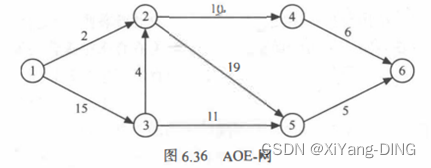
例题1
①求这个工程最早可能在什么时间结束;
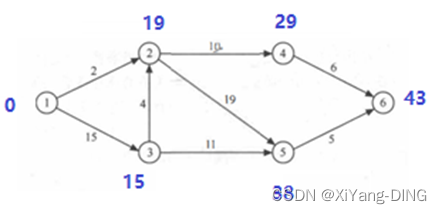
ve(i) vl(i)
1 0
2 19
3 15
4 29
5 38
6 43
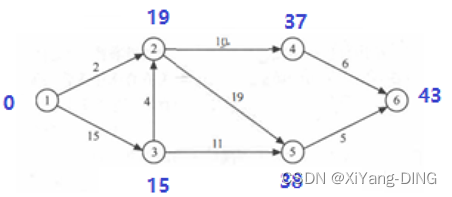
ve(i) vl(i)
1 0 0
2 19 19
3 15 15
4 29 37
5 38 38
6 43 43
最早结束时间:43
②求每个活动的最早开始时间和最早开始时间;
③确定哪些活动是关键活动。
<1,3><3,2><2,5><5,6>
④关键路径
1,3,2,5,6
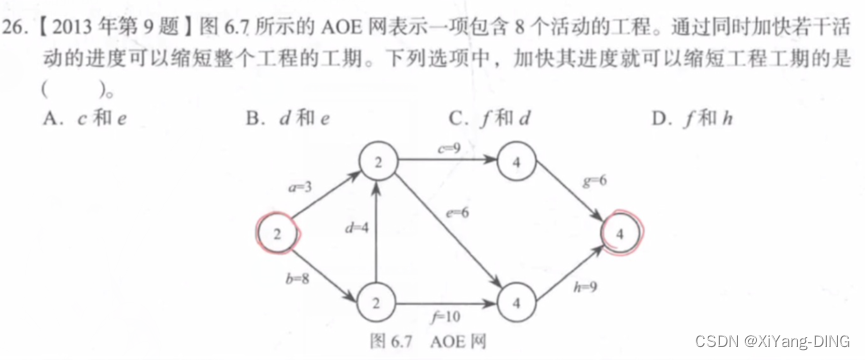
例题2
acg18
aeh 18
bfh 27
bdcg 27
bdeh 27
关键路径:路径长度最长的路径。
答案:C
十六、顺序查找—顺序/折半/分块
1.顺序
(1)普通顺序查找
ASL成功=
(
(
1
+
2
+
3
+
⋯
+
n
)
)
/
n
=
(
1
+
n
)
/
2
((1+2+3+⋯+n))/n=(1+n)/2
((1+2+3+⋯+n))/n=(1+n)/2
ASL不成功=
n
+
1
n+1
n+1
时间复杂度:
O
(
n
)
O(n)
O(n)
(2)有序表的顺序查找
ASL不成功=
(
(
1
+
2
+
3
+
⋯
+
n
+
n
)
)
/
(
n
+
1
)
=
n
/
2
+
n
/
(
n
+
1
)
((1+2+3+⋯+n+n))/(n+1)=n/2+n/(n+1)
((1+2+3+⋯+n+n))/(n+1)=n/2+n/(n+1)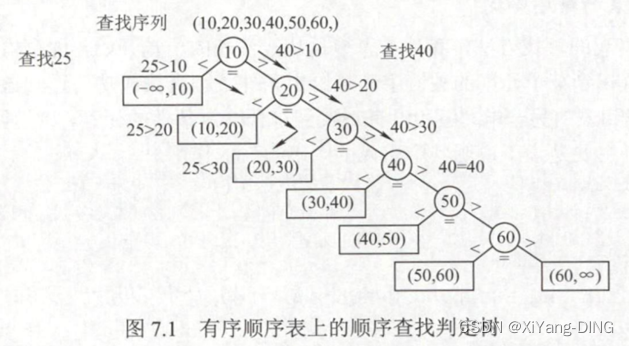
2.折半
要求:线性表必须采用顺序存储结构,而且表中元素按关键字有序排列

ASL成功=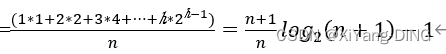
时间复杂度为:$O(log_2 n)$
3.分块
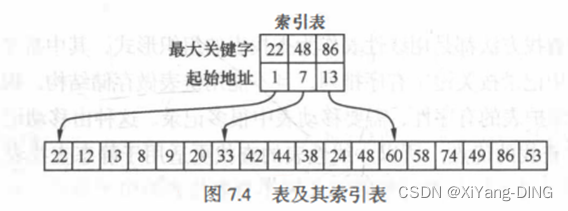
ASL成功= Lb+Lw
Lb为查找索引表确定所在块的平均查找长度,Lw为在块中查找元素的平均查找长度
例题1
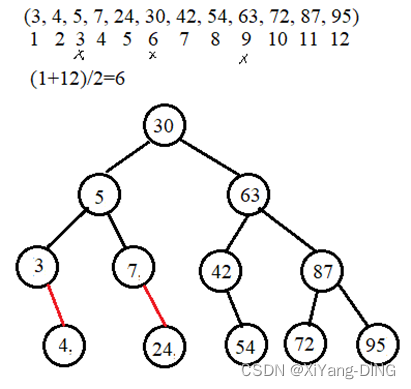
假定对有序表:(3, 4, 5, 7, 24, 30, 42, 54, 63, 72, 87, 95) 进行折半查找,试回答下列问题。(编号从1开始)
①画出描述折半查找过程的判定树。
②若查找元素54, 需依次与哪些元素比较? 30,63,42,54
③若查找元素90, 需依次与哪些元素比较? 30,63,87,95
④假定每个元素的查找概率相等,求查找成功时的平均查找长度。
ASL成功=(11+22+34+45)/12=37/12
十七、树表的查找—BTS/AVL/B/B+
1.二叉排序树(BTS)
(1)定义
①若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
②若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
③它的左、右子树也分别为二叉排序树。
(2)性质
中序遍历一棵二叉树时可以得到一个结点值递增的有序序列
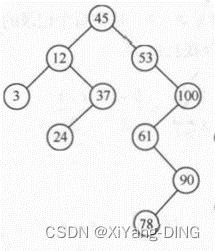
(3)插入
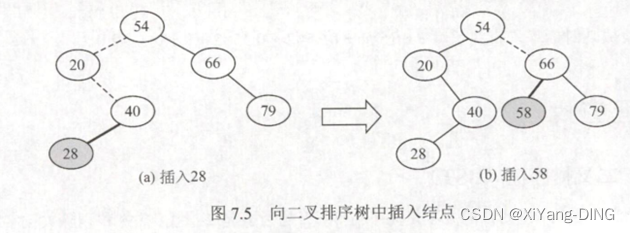
插入一定是叶子结点
(4)构造
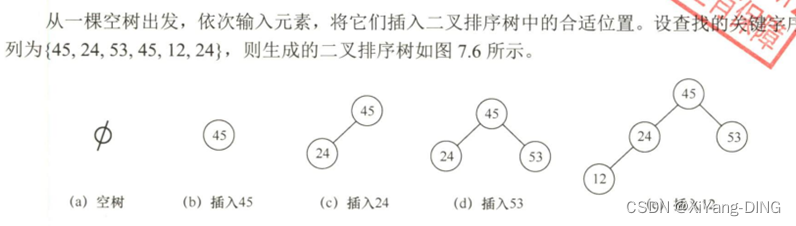
(5)删除
①删叶子,直接删
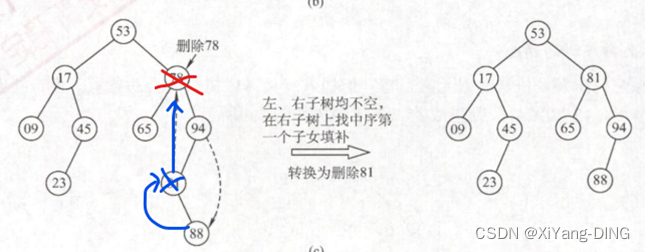
②删无左孩子/无右孩子,孩子替换要删的结点
③删有左右孩子,找中序遍历的直接前驱/后继,替换要删的结点,删去这个前驱/后继,变为①②
【说明】:反正保证二叉排序树中序遍历有序就行

(6)ASL O()
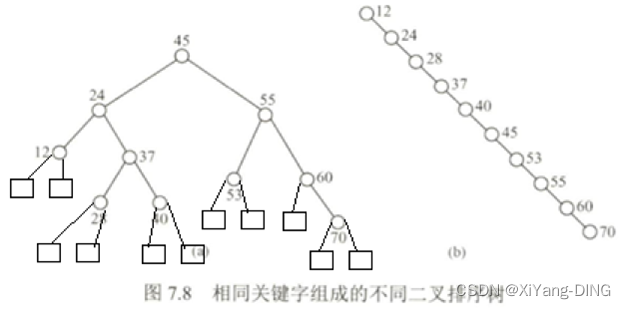
ASLa成功=(11+22+34+43)/10=2.9
ASLa不成功=(35+46)/11=3.545
若二叉排序树左右子树高度只差的绝对值不超过1(平衡二叉树),它的平均查找长度为O(log2n)。
若二叉排序树是一个只有右(左)孩子的单支树(类似于有序的单链表),则其平均查找长度为O(n)。
2.平衡二叉树AVL
(1)定义
结点左子树与右子树的高度差为该结点的平衡因子,则平衡二叉树结点的平衡因子的值只可能是-1、0或1。
(2)插入
从接入的点往上找“最小不平衡子树”的根,找根在这条路径上最近的3个结点调整,调整完剩余结点按定义去放
①LR:
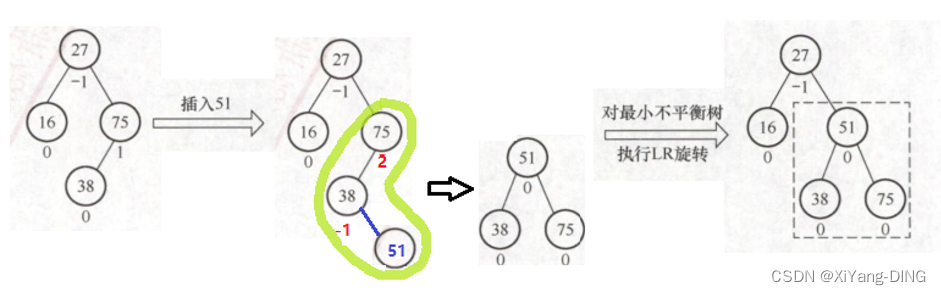
②LL:
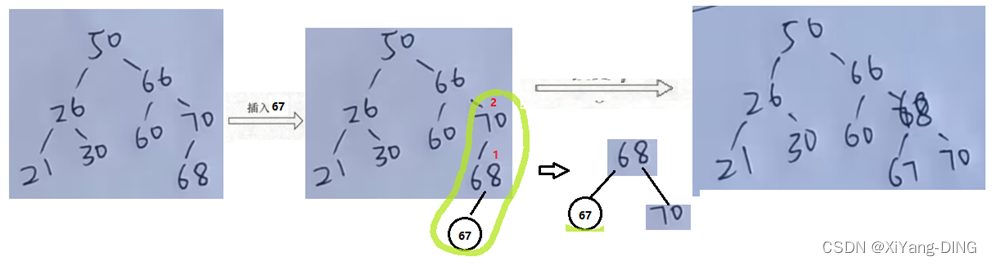
③RR:
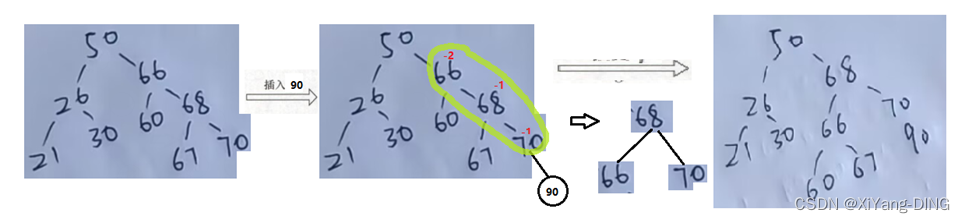
④RL:
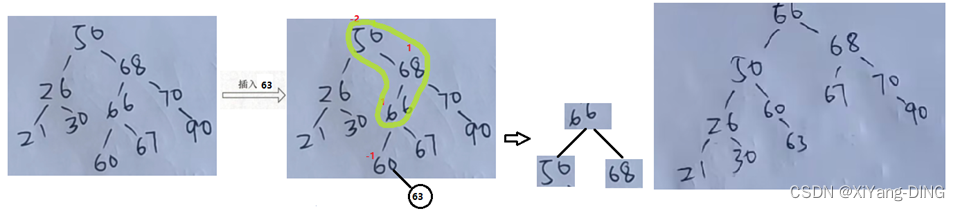
(3)O()
时间复杂度O(log2n)
3.B-树
(1)定义
一棵m阶的B树,或为空树,是所有结点的平衡因子=0的m路平衡查找树
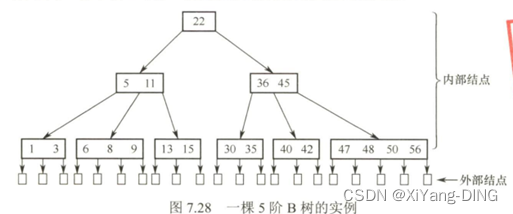
①树中每个结点至多有m棵子树,最多有m-1个关键字
②若根结点不是叶子结点,则至少有两棵子树;
③除根之外的所有非终端结点至少有 个子树,至少含有 个关键字;
④所有的叶子结点都出现在同一层次上,并且不带信息,通常称为失败结点(失败结点并不存在,指向这些结点的指针为空。引入失败结点是为了便于分析B-树的查找性能);
4.B+树
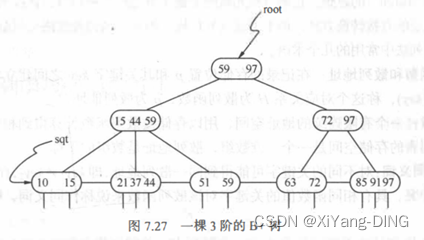
B+树和B-树的差异
(1)有n棵子树的结点中含有n个关键字;
(2)所有的叶子结点中包含了全部关键字的信息,以及指向含这些关键字记录的指针,且叶 子结点本身依关键字的大小自小而大顺序链接;
(3)所有的非终端结点可以看成是索引部分,结点中仅含有其子树(根结点)中的最大(或最小)关键字。
例题1
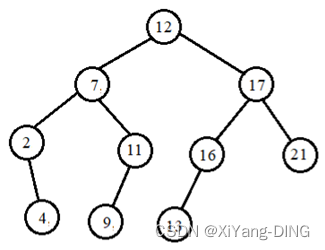
在一棵空的二叉排序树中依次插入关键字序列为 12, 7, 17, 11, 16, 2, 13, 9, 21, 4, 请画出所得到的二叉排序树。
说明:验算办法用中序遍历应得到排序结果:2,4,7,9,11,12,13,16,17,21
十八、散列表—构造/冲突/查找
①散列函数和散列地址:在记录的存储位置p和其关键字key之间建立一个确定的对应关系H, 使p=H(key), 称这个对应关系H为散列函数,p为散列地址。
1.构造方法
除留余数法:假设散列表表长为m, 选择一个不大于m的数p, 用p去除关键字,除后所得余数为散列地址,即H(key) = key%p。一般情况下,可以选p为小于表长的最大质数。
2.处理冲突的方法
(1)开放地址法
H
i
=
(
H
(
k
e
y
)
+
d
i
)
H_i= (H(key) +d_i)%m
Hi=(H(key)+di)
①线性探测法:d_i = l, 2, 3, …, m-1
②二次探测法: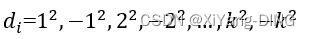
(2)链地址法
3. 查找
查找过程中需和给定值进行比较的关键字的个数取决于三个因素:散列函数、处理冲突 的方法和散列表的装填因子a
列表的装填因子a定义为 a=表中填入的记录数/散列表的长度
例题1
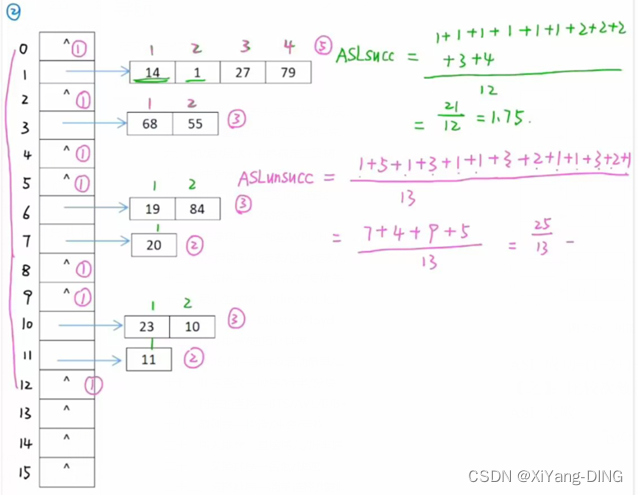
对于的关键字(19, 14, 23, 1, 68, 20, 84, 27, 55, 11, 10, 79), 设散列函数为 H(key)= key %13, 用线性探测法处理冲突。设表长为16, 试构造这组关键字的散列表,并计算查找成功和查找失败时的平均查找长度。
H(19)=6,H(14)=1,H(23)=10
H(1)=1发生冲突,H(1)=(1+1)%13=2
H(68)=3,H(20)=7,H(84)=8
H(27)=1发生冲突,H(27)=(1+1)%13=2发生冲突,H(27)=(1+2)%13=3发生冲突,H(27)=(1+3)%13=4
H(55)=3发生冲突,H(55)=(3+1)%13=4发生冲突,H(55)=(3+2)%13=5
H(11)=11
H(10)=10发生冲突,H(10)=(10+1)%13=11发生冲突, H(10)=(10+2)%13=12
H(79)=1发生冲突,H(79)=(1+1)%13=2发生冲突, H(79)=(1+2)%13=3发生冲突, H(79)=(1+3)%13=4发生冲突, H(79)=(1+5)%13=5发生冲突,….,直到H(79)=(1+8)%13=9散列地址 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
关键字 14 1 68 27 55 19 20 84 79 23 11 10
比较次数 1 2 1 4 3 1 1 3 9 1 1 3
ASL成功=(1+2+1+4+3+1+1+3+9+1+1+3)/12=2.5
比较次数相加/占有散列地址的个数
ASL失败=(1+13+12+11+10+9+8+7+6 +5+4+3+2)/13
0查找1次失败
1查找13次失败,2查找12次失败,
…
对于
注意 1查找失败2次
例题2
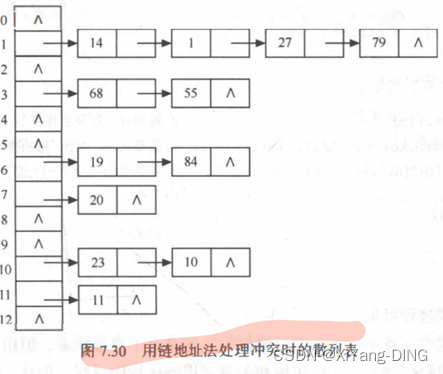
已知一组关键字为 (19, 14, 23, 1, 68, 20, 8 4, 27, 55, 11, 10 , 79), 设散列函数 H(key) = key %13, 用链地址法处理冲突,试构造这组关键字的散列表,计算查找成功和查找失败时的平均查找长度。
例题3
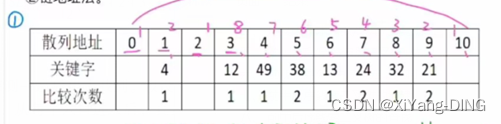
设散列表的地址范围为0~17,散列函数为:H(key)=key%16。用线性探测法处理冲突,输入关键字序列:(10,24,32,17,31,30,46,47,40,63,49),构造散列表,试回答下列问题:
①画出散列表的示意图。
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
关键字 32 17 63 49 24 40 10 30 31 46 47
比较次数 1 1 6 3 1 2 1 1 1 3 3
②若查找关键字63,需要依次与哪些关键字进行比较? 31,46,47,32,17,63
③若查找关键字60,需要依次与哪些关键字进行比较? H(60)=12,与空对比
④假定每个关键字的查找概率相等,求查找成功时的平均查找长度。
ASL成功=(1+1+6+3+1+2+1+1+1+3+3)/11=23/11
例题4
设有一组关键字 (9, 1, 23, 14, 55, 20, 84, 27), 采用散列函数:H(key) = key%7, 表长为 10, 用开放地址法的二次探测法处理冲突。要求:对该关键字序列构造散列表,并计算查找成功的平均查找长度。
H(84)=84%7=0,H(84)=(0+1)%7=1, H(84)=(0-1)%7=6,H(84)=(0+4)%7=4
H(27)=27%7=6,H(27)=(6+1)%7=0, H(27)=(6-1)%7=5
0 1 2 3 4 5 6 7 8 9
关键字 14 1 9 23 84 27 55 20
比较次数 1 1 1 2 4 3 1 2
ASLsucc=(1+1+1+2+4+3+1+2)/8=15/8
例题5
散列函数H(K) = 3K % 11 , 散列地址空间为 0~10, 对关键字序列 (32, 13, 49, 24, 38, 21, 4, 12), 按下述两种解决冲突的方法构造散列表,并分别求出等概率下查找成功时和查找失败时的平均查找长度 ASLsucc和 ASLunsucc
①线性探测法。
0 1 2 3 4 5 6 7 8 9 10
关键字 4 12 49 38 13 24 32 21
比较次数 1 1 1 2 1 2 1 2
ASLsucc=(1+1+1+2+1+2+1+2)/8=11/8
ASLunsucc=(1+2+1+8+7+6+5+4+3+2+1)/11=40/11
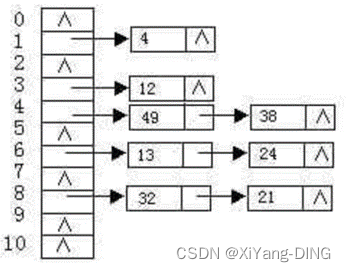
②链地址法。
ASLsucc=(15+23)/8=11/8
ASLunsucc=(16+22+3*3)/11=19/11
十九、插入排序—直接插入/折半插入/希尔
1.直接插入排序
后面没有排好的一个一个往排好的里面丢,比较时候根排好的最后一个元素比

2.折半插入排序
后面没有排好的一个一个往排好的里面丢,比较时候根排好的中间元素比
但对于数据量不很大的排序表,折半插入排序往往能表现出很好的性能。折半插入排序仅减少了比较元素的次数约O(nlogn),元素的移动次数并未改变,它依赖于待排序表的初始状态。
3.希尔排序
Step1.定义增量序列Dk : Dm>Dm-1>…>D1=1(互质)
Step2.对每个Dk进行Dk间隔插入排序
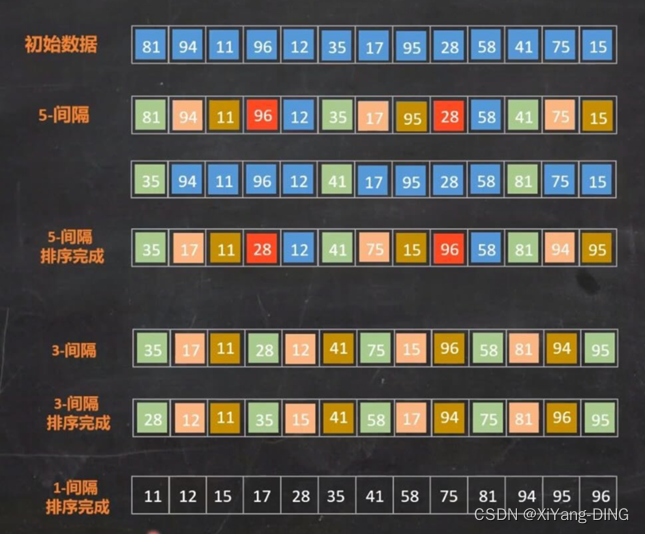
例题1
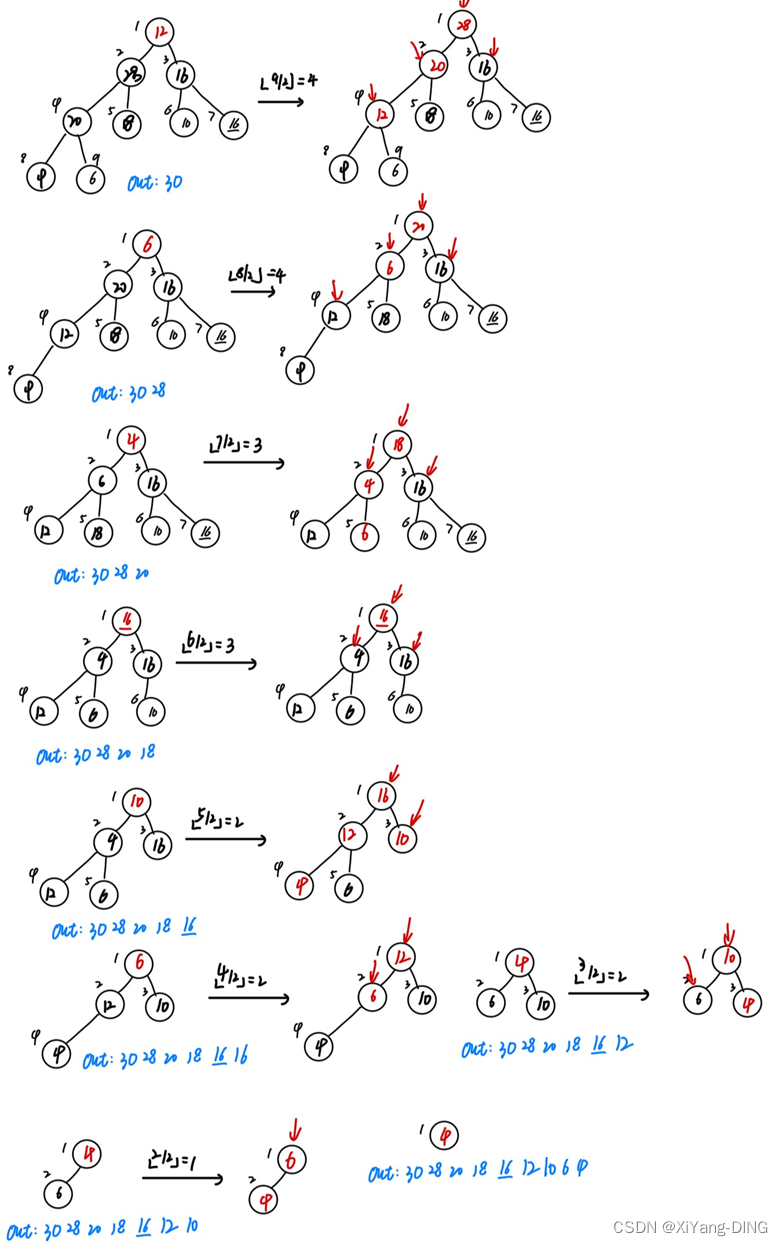
设待排序的关键字序列为{12,2,16,30,28,10,16*,20,6,18}, 试分别写出使用以下排序方法, 每趟排序结束后关键字序列的状态。
①直接插入排序
{12,2,16,30,28,10,16,20,6,18}
第1趟:{(2,12,)16,30,28,10,16,20,6,18}
第2趟:{(2,12,16,)30,28,10,16,20,6,18}
第3趟:{(2,12,16,30,)28,10,16,20,6,18}
第4趟:{(2,12,16,28,30,)10,16,20,6,18}
第5趟:{(2,10,12,16,28,30,)16,20,6,18}
第6趟:{(2,10,12,16,16,28,30,)20,6,18}
第7趟:{(2,10,12,16,16,20,28,30,)6,18}
第8趟:{(2,6,10,12,16,16,20,28,30,)18}
第9趟:{(2,6,10,12,16,16,18,20,28,30)}
②折半插入排序
与①过程一样只是在比较时候比的位置不一样,第一个是最后一个,第二个是中间
③希尔排序(增量选取5,3,1)
增量为5:{12,2,16,30,28,10,16,20,6,18}
{10,2,16,6,18,12,16,20,30,28}
增量为3:{10,2,16,6,18,12,16,20,30,28}
{6,2,12,10,18,16,16,20,30,28}
增量为1:{10,2,16,6,18,12,16,20,30,28}
{2,6,10,12,16,16,18,20,28,30}
二十、交换排序—冒泡/快速
1.冒泡排序
从前两两对比,大的往后放
2.快速排序
例题1
设待排序的关键字序列为{12,2,16,30,28,10,16*,20,6,18}, 试分别写出使用以下排序方法, 每趟排序结束后关键字序列的状态。
①冒泡排序
{12,2,16,30,28,10,16,20,6,18}
第1趟:{2, 12,16, 28, 10, 16,20,6,18,30}
第2趟:{2, 12,16, 10, 16, 20, 6,18, 28,30}
第3趟:{2, 12, 10, 16,16, 6,18, 20, 28,30}
第4趟:{2, 10, 12, 16, 6, 16, 18, 20, 28,30}
第5趟:{2, 10, 12, 6, 16,16, 18, 20, 28,30}
第6趟:{2, 10, 6, 12, 16,16, 18, 20, 28,30}
第7趟:{2, 6, 10, 12, 16,16, 18, 20, 28,30}
第8趟:{2, 6, 10, 12, 16,16, 18, 20, 28,30}
第9趟:{2, 6, 10, 12, 16,16, 18, 20, 28,30}
第10趟:{2, 6, 10, 12, 16,16, 18, 20, 28,30}
②快速排序
{12,2,16,30,28,10,16,20,6,18}
第一趟:
第二趟:
第三趟:
{2,6,10,12,18,16,16,20,28,30}
第四趟:
{2,6,10,12, 16, 16,18,20,28,30}
第五趟:
{2,6,10,12, 16, 16,18,20,28,30}
左子序列递归深度为1,右子序列递归深度为3
二十一、选择排序—简单选择/堆排
1. 简单选择排序
遍历找小的放前面
2. 堆排序
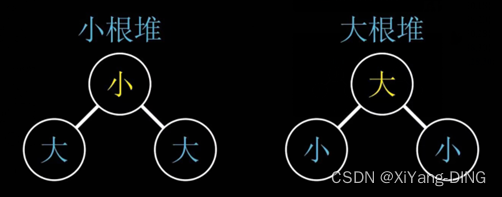
(1)建堆(例题1)
(2)重建堆(堆排序过程)(例题1)
根与最后一个元素换位置,输出最后一个元素(也就是根),然后建堆
例题1
设待排序的关键字序列为{12,2,16,30,28,10,16*,20,6,18}, 试分别写出使用以下排序方法, 每趟排序结束后关键字序列的状态。
①简单选择排序
{12,2,16,30,28,10,16*,20,6,18}
第1趟:{2, 12,16,30,28,10,16,20,6,18}
第2趟:{2,6,12,16,30,28,10,16,20,18}
第3趟:{2,6,10,12,16,30,28,16,20,18}
第4趟:{2,6,10,12,16,30,28,16,20,18}
第5趟:{2,6,10,12,16,30,28,16,20,18}
第6趟:{2,6,10,12,16,16,30,28,20,18}
第7趟:{2,6,10,12,16,16,18,30,28,20}
第8趟:{2,6,10,12,16,16,18,20,30,28}
第9趟:{2,6,10,12,16,16,18,20,28,30}
第10趟:{2,6,10,12,16,16,18,20,28,30}
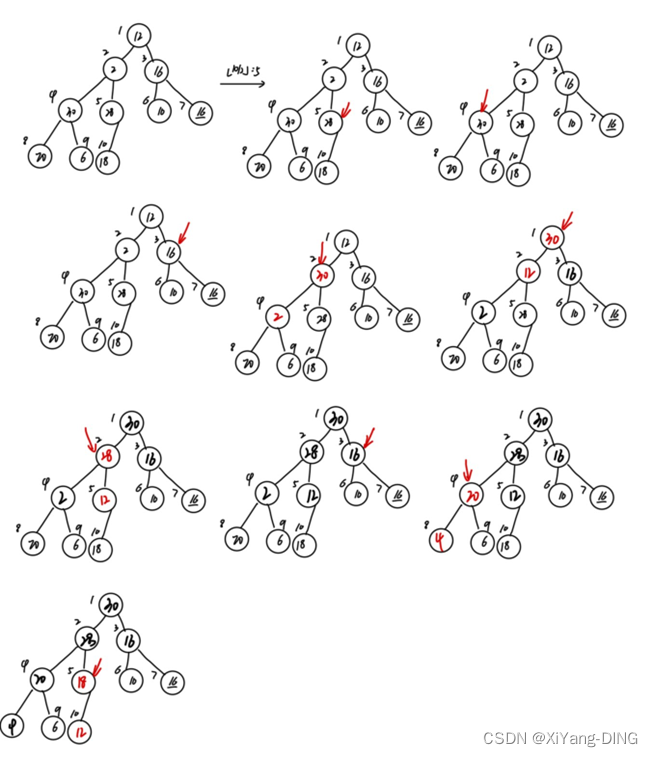
②堆排序
(1)初始堆
(2)重建堆
二十二、归并排序
两路归并就是两个两个排序,排好之后,再四个四个排,以此类推
例题1
设待排序的关键字序列为{12,2,16,30,28,10,16*,20,6,18}, 试分别写出使用以下排序方法, 每趟排序结束后关键字序列的状态。
①二路归并排序
{12,2,16,30,28,10,16*,20,6,18}
第1次:{2,12,16,30,10,28,16*,20,6,18}
{2,12,16,30,10,28,16*,20,6,18}
第2次: {2,12,16,30,10,16*,20,28,6,18}
{2,12,16,30,10,16*,20,28,6,18}
第3次:{2,10,12,16,16*,20,28,30,6,18}
{2,10,12,16,16*,20,28,30,6,18}
第4次:{2,6,10,12,16,16*,18,20,28,30}
二十三、基数排序
例题1
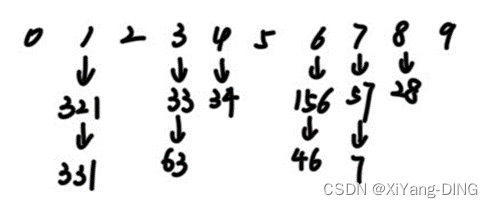
给出如下关键字序列 {321,156, 57, 46, 28, 7,331, 33, 34, 63}, 试按链式基数排序方法, 列出每一趟分配和收集的过程。
第一趟:
分配:
收集:321,331,33,63,34,156,46,57,7,28
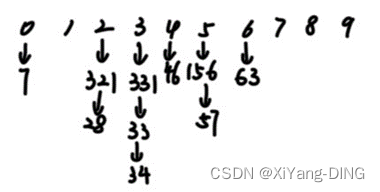
第二趟
分配
收集:7,321,28,331,33,34,46,156,57,63
第三趟
分配
收集:7,28,33,46,57,63,156,321,331
二十四、排序算法时间/空间/稳定性记忆
B站: BV1NL4y1t7Do
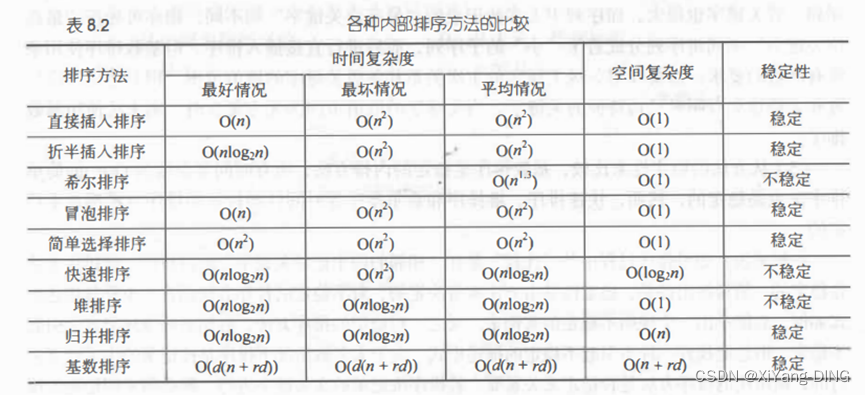
稳定性:插帽龟(插入冒泡归并)🐢,统计鸡(桶排计数基数)🐓
时间复杂度:插帽龟选择帽子插(选择冒泡插入)的时候,恩姓长老就方了(n^2),大喊“快归堆”(快速归并堆排)(logn)