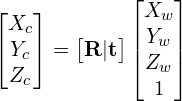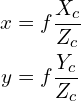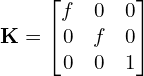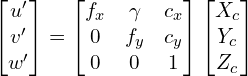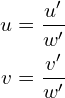Opencv实验合集——实验八：相机校准

1.定义

首先，我们来理解一下怎么从相机的角度去看一张图片，就好比如你用眼睛作为相机来进行摄影，但是比摄影机强的是，你是怎么摄影图片之后再将它矫正出现在你眼前，将歪歪扭扭的图片变成一张在你眼前是一张直的图片

为了轻松理解问题，假设您在房间中部署了一个摄像头。

给定这个房间中的一个 3D 点 P，我们希望在相机拍摄的图像中找到这个 3D 点的像素坐标（u， v），即你眼前对应的二位平面的坐标

现在我们一步步进行推理变换

1.世界坐标系

要定义房间中点的位置，我们需要首先为这个房间定义一个坐标系。它需要两件事

原点：我们可以任意固定房间的一角作为原点（0，0，0）。
X、Y、Z轴：我们还可以沿地板上的二维定义房间的X轴和Y轴，沿垂直墙定义Z轴。

使用上述方法，我们可以通过沿 X、Y 和 Z 轴测量它与原点的距离来找到该房间中任何点的 3D 坐标（Xw,Yw,Zw）。

此坐标系附加到房间称为世界坐标系。在图 1 中，它使用橙色轴显示。我们将使用粗体字体（例如（Xw,Yw,Zw））来显示轴，并使用常规字体来显示点的坐标（例如（Xw,Yw,Zw）)。

通俗来讲就是以上帝视角从一个角落出发，抛开相机，定义一个物体的坐标（Xw,Yw,Zw）

2.相机坐标系

现在，让我们在这个房间里放一个摄像头。

房间的图像将使用此相机捕获，因此，我们对连接到该相机的 3D 坐标系感兴趣。

如果我们将相机放在房间的原点，并对其进行对齐，使其 X、Y 和 Z 轴与房间的Xw,Yw和Zw轴对齐，则两个坐标系将相同。

然而，这是一个荒谬的限制。我们希望将相机放在房间的任何地方，它应该能够看到任何地方。在这种情况下，我们需要找到 3D 房间（即世界）坐标和 3D 相机坐标之间的关系。

假设我们的相机位于房间的任意位置

$（t_X、t_Y、t_Z）$

用技术术语来说，我们可以将相机坐标相对于世界坐标进行平移

$（t_X、t_Y、t_Z）$

相机也可能在看某个任意方向。换句话说，我们可以说相机是相对于世界坐标系旋转的。

3D 旋转是使用三个参数捕获的 -- 您可以将这三个参数视为偏航、俯仰和滚动。你也可以把它看作是3D轴（两个参数）和围绕该轴的角度旋转（一个参数）。

但是，将旋转编码为 3×3 矩阵通常很方便。现在，您可能会认为 3×3 矩阵有 9 个元素，因此有 9 个参数，但旋转只有 3 个参数。这是真的，这就是为什么任何任意的 3×3 矩阵都不是旋转矩阵的原因。在不赘述细节的情况下，现在让我们只知道旋转矩阵只有三个自由度，即使它有 9 个元素。

世界坐标和相机坐标通过旋转矩阵R和 3 元素平移向量相关联平移向量t（t_X、t_Y、t_Z）

这意味着在世界坐标中具有坐标值

$（X_w、Y_w、Z_w）$

的点 P 在照相机坐标系中将具有不同的坐标值

$（X_c、Y_c、Z_c）$

我们使用红色表示相机坐标系。

这两个坐标值通过以下等式相关。

$\begin{公式*} \begin{bmatrix} X_c\\ Y_c\\ Z_c \end{bmatrix}= \mathbf{R} \begin{bmatrix} X_w\\ Y_w\\ Z_w \end{bmatrix} + \mathbf{t} \end{公式*}$

请注意，将旋转表示为矩阵允许我们使用简单的矩阵乘法进行旋转，而不是像偏航、俯仰、滚动等其他表示形式那样需要繁琐的符号操作。我希望这能帮助您理解为什么我们将旋转表示为矩阵。

通俗来说就是通过矩阵相乘，通过世界坐标（Xw,Yw,Zw）旋转加平移变成相机坐标系(Xc,Yc,Zc)

在射影几何中，使用齐次坐标来表示点，它在坐标上添加了一个额外的维度。
世界坐标在等式中使用齐次坐标，这允许在有限数内表示无限量，例如表示无穷远处的点

将 3×1 平移向量作为列附加到 3×3 旋转矩阵的末尾，以获得称为外在矩阵的 3×4 矩阵。

(2)

$\begin{equation*} \begin{bmatrix} X_c\\ Y_c\\ Z_c \end{bmatrix}= \begin{bmatrix} \mathbf{R} |\mathbf{t} \end{bmatrix} \begin{bmatrix} X_w\\ Y_w\\ Z_w \\ 1 \end{bmatrix} \end{公式*}$

其中，外在矩阵P由下式给出

(3)

$\begin{方程*} \mathbf{P} = \begin{bmatrix} \mathbf{R} |\mathbf{t} \end{bmatrix} \end{方程*}$

齐次坐标：在射影几何中，我们经常使用有趣的坐标表示，其中在坐标上附加了一个额外的维度。笛卡尔坐标中的 3D 点

$（X、Y、Z）$

可以写成

$（X、Y、Z、1）$

齐次坐标。更一般地说，齐次坐标中的点与笛卡尔坐标

$（X、Y、Z、W）$

中的点

$（X/W、Y/W、Z/W）$

相同。齐次坐标允许我们使用有限数来表示无限量。例如，无穷远处的点可以表示为

$(1, 1, 1, 0)$

齐次坐标。您可能会注意到，我们在等式 2 中使用了齐次坐标来表示世界坐标。

3.图像坐标系

现在则需要将相机坐标系中的3D坐标投影成投影面的2D坐标

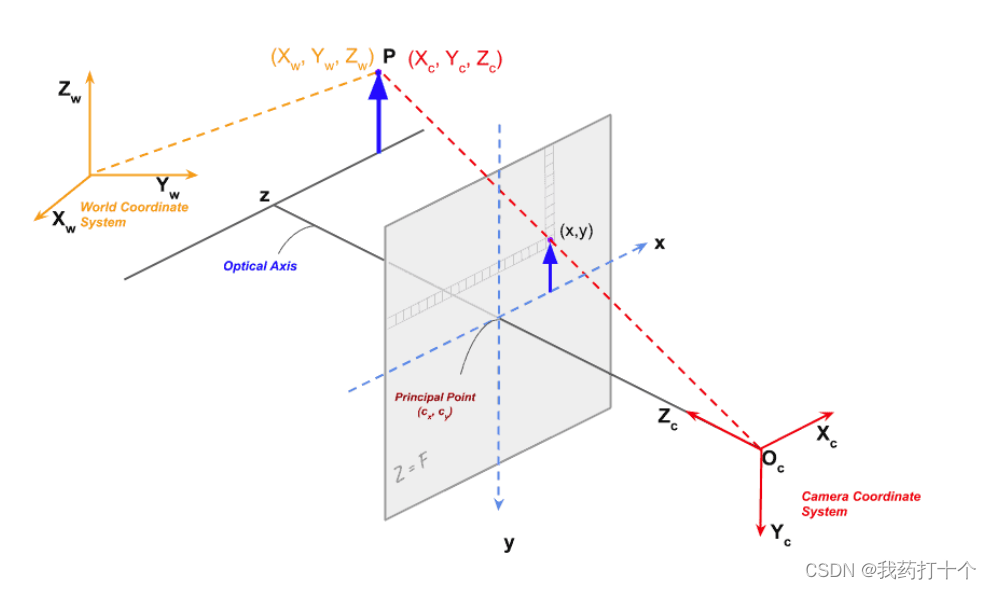
一旦我们通过对点世界坐标应用旋转和平移在相机的 3D 坐标系中得到一个点，我们就可以将该点投影到图像平面上以获得该点在图像中的位置。

在上图中，我们看到的是相机坐标系

$（X_c、Y_c、Z_c）$

中坐标为坐标的点 P。提醒一下，如果我们不知道这个点在相机坐标系中的坐标，我们可以使用外在矩阵变换它的世界坐标，从而使用公式获得相机坐标系中的坐标。

光学中心（针孔）用Oc表示。实际上，该点的倒置图像是在图像平面上形成的。为了数学上的方便，我们简单地进行所有计算，就好像图像平面在光学中心的前面一样，因为从传感器读出的图像可以微不足道地旋转 180 度以补偿反转。在实践中，即使这不是必需的。读者奥拉夫·彼得斯（Olaf Peters）在评论部分指出：“这甚至更简单：真正的相机传感器只是以相反的顺序（从右到左）从最底层的一行读出，然后从每一行从下到上读出。通过这种方法，图像自动直立形成，左右顺序正确。因此，在实践中，不再需要旋转图像。

将图像平面放置在距光学中心一定距离 f (焦距)处。使用高中几何图形（相似三角形），我们可以显示由下式给出的3D点

$（Xc、Yc、Zc）$

的投影图像(x,y)

$\begin{align*} x &= f \frac{X_c}{Z_c} \\ y &= f \frac{Y_c}{Z_c} \end{align*}$

上面两个方程可以用矩阵形式改写如下

$\begin{align*} \begin{bmatrix} x' \\ y' \\ z' \end{bmatrix} = \begin{bmatrix} f & 0 & 0 \\ 0 & f & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X_c\\ Y_c\\ Z_c \end{bmatrix} \end{align*}$

下面K显示的矩阵称为内在矩阵，包含相机的内在参数。

$\begin{align*} \mathbf{K} = \begin{bmatrix} f & 0 & 0 \\ 0 & f & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{align*}$

上面的简单矩阵仅显示了焦距。

特殊情况：如果相机不是正方形的，则x方向和y方向的焦距不相等，

因此我们可能有两种不同的焦距 fx 和 fy 相机的光学中心 (Cx,Cy) 可能与图像坐标系的中心不重合

考虑到以上所有因素，相机矩阵可以重写为。

$\begin{align*} \mathbf{K} = \begin{bmatrix} f_x & \gamma & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \end{align*}$

让我们用 (u,v)表示图像坐标。

$\begin{align*} \begin{bmatrix} u' \\ v' \\ w' \end{bmatrix} = \begin{bmatrix} f_x & \gamma & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X_c\\ Y_c\\ Z_c \end{bmatrix} \end{align*}$

$\begin{align*} u &= \frac{u'}{w'}\\ v &= \frac{v'}{w'} \end{align*}$

总结

将世界坐标系中的 3D 点投影到相机像素坐标分两步完成。

使用外部矩阵将 3D 点从世界坐标转换为相机坐标，该矩阵由两个坐标系之间的旋转和平移组成。
相机坐标系中的新 3D 点使用内在矩阵投影到图像平面上，该矩阵由内部相机参数（如焦距、光学中心等）组成。

2.相关的函数方法

cv.findChessboardCorners 是OpenCV库中用于在图像中检测棋盘格角点的函数。这个函数主要用于相机标定，其中通过检测棋盘格的角点，可以估计相机的内部参数（如焦距、主点坐标等）和外部参数（相机的姿态）

ret, corners = cv.findChessboardCorners(image, patternSize, corners, flags)

image: 输入的图像，通常是灰度图像。
patternSize: 棋盘格的尺寸，是一个二元组 (columns, rows)，表示棋盘格的列数和行数。
corners: 用于存储检测到的角点的输出变量，通常是一个NumPy数组。
flags: 用于指定额外的标志，例如角点的搜索精度等。

返回值：

ret: 一个布尔值，表示是否成功找到了棋盘格的角点。如果找到了，ret为True；否则为False。
corners: 一个包含检测到的角点坐标的NumPy数组。

寻找角点的方法不仅仅限于 cv.findChessboardCorners。OpenCV 提供了多种寻找角点的方法，具体选择取决于场景和应用的需求。以下是一些常用的寻找角点的方法：

cv.findChessboardCorners：

适用于拍摄包含棋盘格的图像，尤其是用于相机标定的情况。

cv.findCirclesGrid：

用于在图像中寻找圆形的格子，通常用于相机标定。

cv.goodFeaturesToTrack：

基于角点响应的方法，用于在图像中检测最强的角点。

cv.cornerHarris：

使用Harris角点检测方法，在图像中找到角点。

cv.cornerMinEigenVal：

类似于 cv.goodFeaturesToTrack，也是一种角点检测方法。

cv.cornerSubPix：

在已知的角点位置周围进行亚像素级别的角点精细调整。

cv.SimpleBlobDetector：

用于检测二值图像中的斑点或小的圆形物体，适用于一些计算机视觉应用。

cv.cornerSubPix 是OpenCV库中的一个函数，用于对由 cv.findChessboardCorners 等角点检测函数找到的初始角点坐标进行亚像素级别的精细调整。该函数通常在进行相机标定时使用，以提高角点坐标的准确性

cv.cornerSubPix(image, corners, winSize, zeroZone, criteria)

image: 输入的灰度图像。
corners: 初始角点坐标，通常是通过角点检测函数（如 cv.findChessboardCorners）得到的。
winSize: 用于搜索最佳角点位置的窗口大小。
zeroZone: 在搜索过程中忽略的中心区域。
criteria: 迭代终止的条件。

返回值：

调整后的角点坐标

cv.drawChessboardCorners 是OpenCV库中的一个函数，用于在图像上绘制检测到的棋盘格角点。该函数通常与角点检测函数（如 cv.findChessboardCorners）一起使用，以便在标定相机时可视化检测到的角点。

cv.drawChessboardCorners(image, patternSize, corners, patternWasFound)

image: 输入的图像，通常是彩色图像。
patternSize: 棋盘格的尺寸，是一个二元组 (columns, rows)，表示棋盘格的列数和行数。
corners: 由角点检测函数（例如 cv.findChessboardCorners）找到的角点坐标。
patternWasFound: 一个布尔值，表示是否成功找到了棋盘格

cv.calibrateCamera 是OpenCV中用于相机标定的函数。相机标定是确定相机内部参数和外部参数的过程，包括焦距、主点坐标、畸变系数以及相机的姿态等信息。标定是摄像机应用中重要的一步，可以用于纠正图像畸变、进行三维重建等应用。

retval, cameraMatrix, distCoeffs, rvecs, tvecs = cv.calibrateCamera(objectPoints, imagePoints, imageSize, cameraMatrix, distCoeffs, rvecs, tvecs, flags)

objectPoints: 世界坐标系中的点的坐标，通常是一个包含三维点的列表。
imagePoints: 对应于 objectPoints 的图像上的点的坐标，通常是一个包含二维点的列表。
imageSize: 输入图像的尺寸，通常是一个包含图像宽度和高度的元组。
cameraMatrix: 相机内部参数矩阵，输出标定过程中估计得到的相机内部参数。
distCoeffs: 畸变系数，输出标定过程中估计得到的径向和切向畸变参数。
rvecs: 旋转向量的数组，输出相机外部参数中的旋转向量。
tvecs: 平移向量的数组，输出相机外部参数中的平移向量。
flags: 标定过程中的额外标志，用于指定标定的一些选项。

返回值：

retval: 标定的重投影误差。

cv.getOptimalNewCameraMatrix 是OpenCV库中用于计算优化的新相机内部参数矩阵的函数。这个函数通常在图像畸变矫正时使用，以进一步调整相机内部参数，从而获得更好的校正效果。

newCameraMatrix, validPixROI = cv.getOptimalNewCameraMatrix(cameraMatrix, distCoeffs, imageSize, alpha, newImageSize)

cameraMatrix: 原始相机的内部参数矩阵，通常是通过相机标定得到的。
distCoeffs: 相机的畸变系数，也是通过相机标定得到的。
imageSize: 输入图像的尺寸，通常是一个包含图像宽度和高度的元组。
alpha: 控制视场的缩放因子。当 alpha=0 时，返回的新相机内部参数矩阵仅包含有效像素；当 alpha=1 时，返回的新相机内部参数矩阵包含完整的像素。
newImageSize: 可选参数，新图像的尺寸。如果为 None，则使用输入图像的尺寸。

返回值：

newCameraMatrix: 优化后的新相机内部参数矩阵。
validPixROI: 一个元组，包含四个整数值，表示新图像中包含有效像素的矩形区域。

cv.undistort 是OpenCV库中用于图像畸变矫正的函数。在相机标定过程中，我们通常会估计相机的内部参数和畸变系数。cv.undistort 函数通过这些标定参数，对图像进行畸变矫正，使图像中的直线和形状更加真实，减少由于相机畸变引起的形变

undistorted_image = cv.undistort(src, cameraMatrix, distCoeffs, newCameraMatrix)

src: 输入图像，即待矫正的图像。
cameraMatrix: 相机的内部参数矩阵，通常是通过相机标定得到的。
distCoeffs: 相机的畸变系数，也是通过相机标定得到的。
newCameraMatrix: 可选参数，新的相机内部参数矩阵，用于进一步调整视场。如果为 None，则使用原始相机内部参数矩阵。

返回值：

undistorted_image: 矫正后的图像。

3.代码演示

import numpy as np
import cv2 as cv
import glob

# 终止标准
criteria = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 30, 0.001)

# 准备对象点, 如 (0,0,0), (1,0,0), (2,0,0) ....,(6,5,0)
objp = np.zeros((6*7,3), np.float32)
objp[:,:2] = np.mgrid[0:7,0:6].T.reshape(-1,2)

# 用于存储所有图像对象点与图像点的矩阵
objpoints = [] # 在真实世界中的 3d 点 
imgpoints = [] # 在图像平面中的 2d 点

images = glob.glob('*.jpg')

for fname in images:
    img = cv.imread(fname)
    gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)

    # 找到棋盘上所有的角点
    ret, corners = cv.findChessboardCorners(gray, (7,6), None)

    # 如果找到了，便添加对象点和图像点(在细化后)
    if ret == True:
        objpoints.append(objp)

        corners2 = cv.cornerSubPix(gray,corners, (11,11), (-1,-1), criteria)
        imgpoints.append(corners)

        # 绘制角点
        cv.drawChessboardCorners(img, (7,6), corners2, ret)
        cv.imshow('img', img)
        cv.waitKey(500)

cv.destroyAllWindows()

矫正

import numpy as np
import cv2 as cv
import glob

# 终止标准
criteria = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 30, 0.001)

# 准备对象点, 如 (0,0,0), (1,0,0), (2,0,0) ....,(6,5,0)
objp = np.zeros((6*7,3), np.float32)
objp[:,:2] = np.mgrid[0:7,0:6].T.reshape(-1,2)

# 用于存储所有图像对象点与图像点的矩阵
objpoints = [] # 在真实世界中的 3d 点 
imgpoints = [] # 在图像平面中的 2d 点

images = glob.glob('*.jpg')

for fname in images:
    img = cv.imread(fname)
    gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)

    # 找到棋盘上所有的角点
    ret, corners = cv.findChessboardCorners(gray, (7,6), None)

    # 如果找到了，便添加对象点和图像点(在细化后)
    if ret == True:
        objpoints.append(objp)

        corners2 = cv.cornerSubPix(gray,corners, (11,11), (-1,-1), criteria)
        imgpoints.append(corners)

        # 绘制角点
        cv.drawChessboardCorners(img, (7,6), corners2, ret)
        ret, mtx, dist, rvecs, tvecs = cv.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)
        img2 = cv.imread(fname)
        h, w = img.shape[:2]
        newcameramtx, roi = cv.getOptimalNewCameraMatrix(mtx, dist, (w, h), 1, (w, h))
        # 矫正
        dst = cv.undistort(img2, mtx, dist, None, newcameramtx)

        # 裁切图像
        x, y, w, h = roi
        dst = dst[y:y + h, x:x + w]
        cv.imwrite('calibresult.png', dst)

cv.destroyAllWindows()

4.总结

总结一下上面的叙述，首先是理解整个相机校准的原理，然后是通过代码进行进一步叙述，首先还是检测角点，如果是棋盘检测可以用上面的代码，也有很多其他检测角点的方法在上面简单提了一下，然后是通过角点位置，包括3d点（世界坐标系中的三维点）和2d点位置（图像检测出的角点坐标），接着利用calibrateCamera计算相机参数（旋转，平移等），最后通过计算出的相机参数来矫正图片，使得图片尽量在平面上是以平面的形式展示。注意：检测角点和计算相机参数都需要通过额外的方法来修正。

下面简单演示一下用Harris检测角点的效果

import numpy as np
import cv2 as cv

# 终止标准
criteria = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 30, 0.001)

# 准备对象点，如 (0,0,0), (1,0,0), (2,0,0) ....,(6,5,0)
objp = np.zeros((6*7,3), np.float32)
objp[:,:2] = np.mgrid[0:7,0:6].T.reshape(-1,2)

# 用于存储所有图像对象点与图像点的矩阵
objpoints = [] # 在真实世界中的 3D 点
imgpoints = [] # 在图像平面中的 2D 点

# 图像路径
image_path = r'C:\Users\xiaoou\Desktop\picture\chess.jpg'

# 读取图像
img = cv.imread(image_path)
gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)

# 使用 cornerHarris 找到角点
dst = cv.cornerHarris(gray, 2, 3, 0.04)
print(dst.shape)
# 通过阈值筛选角点
img[dst > 0.01 * dst.max()] = [0, 0, 255]

# 寻找非零像素的坐标
y, x = np.nonzero(dst > 0.01 * dst.max())

# 将坐标转换为图像点格式
corners = np.vstack([x, y]).T.reshape(-1, 1, 2).astype(np.float32)

# 如果找到了，便添加对象点和图像点(在细化后)

if corners.shape[0] >= 42:
    # print(objp.shape)
    # print(corners.shape)
    objpoints.append(objp)
    imgpoints.append(corners[:42])

    # 绘制角点
    cv.drawChessboardCorners(img, (7, 6), corners, True)
    cv.imshow('img', img)
    cv.waitKey(0)