系列文章目录
机器学习(一) -- 概述
机器学习(二) -- 数据预处理(1-3)
机器学习(三) -- 特征工程(1-2)
机器学习(四) -- 模型评估(1-4)
未完待续……
目录
机器学习(四) -- 模型评估(1)
机器学习(四) -- 模型评估(2)
机器学习(四) -- 模型评估(3)
---
目录
系列文章目录
前言
四、 聚类模型评估指标
1、外部指标
1.1、兰德指数(RI,Rand index)
1.1.1、调整兰德指数(Adjusted Rand index)
1.2、基于互信息的分数(MI,Mutual Information-based Score)
1.2.1、标准化互信息(NMI,Normalized Mutual Information)
1.2.2、调整互信息(AMI,Adjusted mutual information)
1.3、同质性(Homogeneity Score)和完整性(Completeness Score)以及其调和平均(V-measure)
1.3.1、同质性(Homogeneity Score)
1.3.2、完整性(Completeness Score)
1.3.3、V-measure
1.4、Fowlkes-Mallows Scores(FMI)
2、内部指标
2.1、轮廓系数(Silhouette Coefficient)
2.2、Calinski-Harabaz指数(Calinski-Harabaz Index,也称Variance Ratio Criterion)
2.3、戴维森堡丁指数(DBI,Davies-Bouldin Index)
3、总结
前言
tips:这里只是总结,不是教程哈。
“***”开头的是给好奇心重的宝宝看的,其实不太重要可以跳过。
此处以下所有内容均为暂定,因为我还没找到一个好的,让小白(我自己)也能容易理解(更系统、嗯应该是宏观)的讲解顺序与方式。
第一文主要简述了一下机器学习大致有哪些东西(当然远远不止这些),对大体框架有了一定了解。接着我们根据机器学习的流程一步步来学习吧,掐掉其他不太用得上我们的步骤,精练起来就4步(数据预处理,特征工程,训练模型,模型评估),其中训练模型则是我们的重头戏,基本上所有算法也都是这一步,so,这个最后写,先把其他三个讲了,然后,在结合这三步来进行算法的学习,兴许会好点(个人拙见)。
衡量模型泛化能力的评价标准就是性能度量(模型评估指标、模型评价标准),而针对不同的任务有不同的评价指标。按照数据集的目标值不同,可以把模型评估分为分类模型评估、回归模型评估和聚类模型评估。
四、 聚类模型评估指标
聚类试图将数据集中的样本划分为若干个通常是互不相交的子集,每个子集叫做一个“簇”(cluster),好的聚类算法,一般要求类簇具有:
簇内 (intra-cluster) 相似度高
簇间 (inter-cluster) 相似度低
即同一簇尽可能相似,不同簇尽可能不同。
聚类性能度量大致有两种,
一类是指当数据集的外部信息可用时,通过比较聚类划分与外部准则的匹配度,可以评价不同聚类算法的性能。即将聚类结果于某个“参考模型”(真实值)进行比较。称为“外部指标”(external index);
另一类主要基于数据集的集合结构信息从紧致性、分离性、连通性和重叠度等方面对聚类划分进行评价。即基于数据聚类自身进行评估的。称为“内部指标”(internal index).
外部指标:【兰德指数(RI,Rand index)、调整兰德指数(Adjusted Rand index)】、
【基于互信息的分数(MI,Mutual Information-based Score)、标准化互信息(NMI,Normalized Mutual Information)、调整互信息(AMI,Adjusted mutual information)】、
【同质性(Homogeneity Score)和完整性(Completeness Score)以及其调和平均(V-measure)】、
【Fowlkes-Mallows Scores(FMI)】
内部指标:
轮廓系数(Silhouette Coefficient)、Calinski-Harabaz指数(Calinski-Harabaz Index,也称Variance Ratio Criterion)、戴维森堡丁指数(DBI,Davies-Bouldin Index)
1、外部指标
首先需要定义几个变量:
(可以理解为聚类给出的簇,就是你的模型计算出来的结果,参考模型给出的簇,就是“真实”的簇,实际应该分成这个样子。)。

举个例子,参考模型给出的簇与聚类模型给出的簇划分如下:
编号: 1, 2, 3, 4, 5, 6
聚类簇: 0, 0, 1, 1, 2, 2
参考簇: 0, 0, 0, 1, 1, 1
那么满足a的样本对就是(1,2)、(5,6)【1号和2号的聚类簇都是0,参考簇都是0;5号和6号的聚类簇都是2,参考簇都是1】,总共有两个样本对满足a,所以a=2。
同理,满足b的样本对是(3,4)【3号和4号聚类簇都是1,但参考簇不同】,所以b=1。
同理,满足c的样本对是(1,3)(2,3)(4,5)(4,6)【他们分别都是聚类簇不同,参考簇相同】,所以c=4。
同理,满足d的样本对是(1,4)(1,5)(1,6)(2,4)(2,5)(2,6)(3,5)(3,6)【他们分别聚类簇不同,参考簇也不同】,所以d=8。
用代码展示大概就是这个样子。
# 聚类模型给出的簇
y_predict=[0,0,1,1,2,2]
# 参考模型给出的簇
y_true=[0,0,0,1,1,1]
# 计算abcd
def get_abcd(y_predict,y_true):
a=b=c=d=0
for i in range(0,(len(y_predict)-1)):
for j in range(i+1,len(y_predict)):
if(y_predict[i]==y_predict[j])&(y_true[i]==y_true[j]):
a=a+1;
if(y_predict[i]==y_predict[j])&(y_true[i]!=y_true[j]):
b=b+1;
if(y_predict[i]!=y_predict[j])&(y_true[i]==y_true[j]):
c=c+1;
if(y_predict[i]!=y_predict[j])&(y_true[i]!=y_true[j]):
d=d+1;
return a,b,c,d
a,b,c,d=get_abcd(y_predict,y_true)
print(a,',',b,',',c,',',d)
1.1、兰德指数(RI,Rand index)
兰德指数衡量的是聚类算法将数据点分配到聚类中的准确程度。兰德指数的范围从0到1,1的值表示两个聚类完全相同,接近0的值表示两个聚类有很大的不同。兰德指数只能用于评估将样本点分成两个簇的聚类算法。
公式:
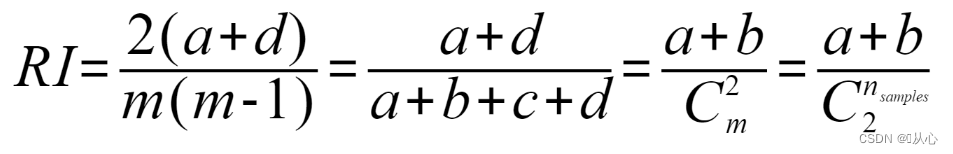
其中 ![]() 和
和![]() 都是表示任意两个样本为一类有多少种组合,是数据集中可以组成的总元素对数。
都是表示任意两个样本为一类有多少种组合,是数据集中可以组成的总元素对数。
用刚才的例子计算出来的结果就是 ![]()
API:
from sklearn.metrics import rand_score
rand_score(y_true,y_predict) 
1.1.1、调整兰德指数(Adjusted Rand index)
未调整的兰德指数类取值区间为[ 0,1],没有一个固定的值表示两个随即标签的关系 ;调整的兰德指数将评分规范到了[−1, 1] 之间,以0.0表示两个随机标签的关系。其中值越接近1表示聚类结果越准确,值越接近0表示聚类结果与随机结果相当,值越接近-1表示聚类结果与真实类别完全相反。
完美的标签的得分为1.0,无相关标签的得分是负数或接近于0.0分。
公式:

其中E(RI)是兰德系数的期望值。【其实就和归一化有点像(不完全一样哈)--死去的记忆突然攻击QwQ】
API:
from sklearn.metrics import adjusted_rand_score
adjusted_rand_score(y_true,y_predict)
调整兰德系数是对称的,交换参数不会改变得分。
1.2、基于互信息的分数(MI,Mutual Information-based Score)
衡量的是聚类结果与真实标签之间的相似性。基于互信息的分数的取值范围为[0,1],其中值越接近1表示聚类结果越准确,值越接近0表示聚类结果与随机结果相当,值越小表示聚类结果与真实类别之间的差异越大。基于互信息的分数是一种相对指标,它的取值受到真实类别数量的影响。当真实类别数量很大时,基于互信息的分数可能会受到偏差。
公式:
假设U与V是对N个样本标签的分配情况。

![]()
API:
from sklearn.metrics import mutual_info_score
mutual_info_score(y_true,y_predict)
1.2.1、标准化互信息(NMI,Normalized Mutual Information)
公式:
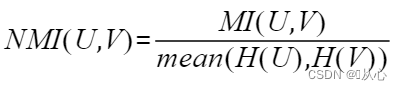
假设U与V是对N个样本标签的分配情况,则两种分布的熵(熵表示的是不确定程度):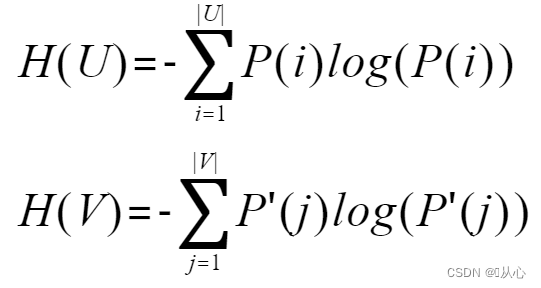
API:
from sklearn.metrics import normalized_mutual_info_score
normalized_mutual_info_score(y_true,y_predict) 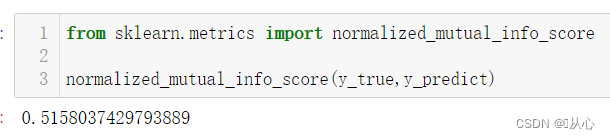
1.2.2、调整互信息(AMI,Adjusted mutual information)
公式:

API:
from sklearn.metrics import adjusted_mutual_info_score
adjusted_mutual_info_score(y_true,y_predict)
!!!注意:MI,NMI,AMI这三个的参数也是对称的,互换不影响结果。
1.3、同质性(Homogeneity Score)和完整性(Completeness Score)以及其调和平均(V-measure)
1.3.1、同质性(Homogeneity Score)
每个簇只包含一个类的成员
公式:

API:
from sklearn.metrics import homogeneity_score
homogeneity_score(y_true,y_predict)
1.3.2、完整性(Completeness Score)
给定类的所有成员都分配给同一个簇
公式:

API:
from sklearn.metrics import completeness_score
completeness_score(y_true,y_predict)
1.3.3、V-measure
V-measure是同质性homogeneity和完整性completeness的调和平均数。
公式:

API:
from sklearn.metrics import v_measure_score
v_measure_score(y_true,y_predict)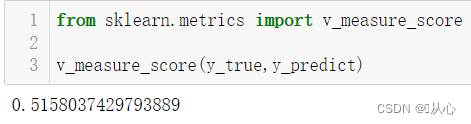
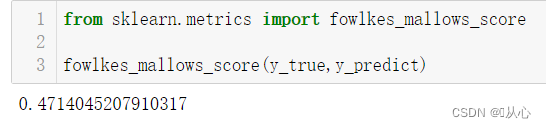
1.4、Fowlkes-Mallows Scores(FMI)
FMI是Precision(精度)和 Recall(召回)的几何平均数。取值范围为 [0,1],越接近1越好。
公式:

API:
from sklearn.metrics import fowlkes_mallows_score
fowlkes_mallows_score(y_true,y_predict)2、内部指标
2.1、轮廓系数(Silhouette Coefficient)
轮廓分数使用同一聚类中的点之间的距离,以及下一个临近聚类中的点与所有其他点之间的距离来评估模型的表现。它主要基于样本点与其所属簇内和最近邻簇之间的距离、相似性和紧密度等因素来计算。数值越高,模型性能越好。轮廓系数的取值范围是[-1,1],同类别样本距离越相近,不同类别样本距离越远,值越大。当值为负数时,说明聚类效果很差。
公式:

其中:
a:样本与同一类别中所有其他点之间的平均距离。
b:样本与下一个最近的簇中所有其他点之间的平均距离。
API:
from sklearn.metrics import silhouette_scorefrom sklearn.datasets import load_iris
# 加载数据
iris=load_iris()
from sklearn.cluster import KMeans
# 模型训练
kmeans_model = KMeans(n_clusters=3, random_state=1).fit(iris.data)
labels = kmeans_model.labels_
from sklearn.metrics import silhouette_score
# 轮廓系数
silhouette_score(iris.data,labels)
2.2、Calinski-Harabaz指数(Calinski-Harabaz Index,也称Variance Ratio Criterion)
通过计算类中各点与类中心的距离平方和来度量类内的紧密度,通过计算各类中心点与数据集中心点距离平方和来度量数据集的分离度,CH指标由分离度与紧密度的比值得到。从而,CH越大代表着类自身越紧密,类与类之间越分散,即更优的聚类结果。
公式:

API:
from sklearn.metrics import calinski_harabasz_score
calinski_harabasz_score(iris.data,labels)
2.3、戴维森堡丁指数(DBI,Davies-Bouldin Index)
是计算任意两类别的类内距离平均距离之和除以两聚类中心距离求最大值。DB越小,意味着类内距离越小同时类间距离越大。零是可能的最低值,接近零的值表示更好的分区。
公式:
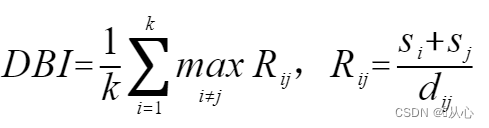
API:
from sklearn.metrics import davies_bouldin_score
davies_bouldin_score(iris.data,labels)
3、总结
外部指标:
Rand Index:用于衡量聚类结果和真实标签之间的相似度。
Adjusted Rand Score:Rand Index的调整版本,可以对随机结果进行惩罚。
Mutual Information Score:衡量聚类结果和真实标签之间的相似度。
Normalized Mutual Information Score:Mutual Information Score的归一化版本。
Adjusted Mutual Information Score:Normalized Mutual Information Score的调整版本。
Homogeneity and Completeness Score:分别衡量聚类结果的同质性和完整性。
V-Measure:基于Homogeneity和Completeness Score计算的综合评估指标。
Fowlkes-Mallows Score:用于衡量聚类结果和真实标签之间的相似度。
内部指标:
Silhouette Score:用于衡量聚类结果中每个样本点与自身簇和其他簇之间的相似度。
Calinski-Harabasz Index:基于簇内和簇间方差之间的比值来计算聚类性能。
Davies-Bouldin Index:基于簇内的紧密度和簇间的分离度来计算聚类性能。
一般情况下,主要是对无标签的数据进行聚类操作。如果在评价中用到外部指标,就需通过人工标注等方法获取标签,成本较高,因此内部指标的实际实用性更强。




![[C#]winform部署yolov5-onnx模型](https://img-blog.csdnimg.cn/direct/dd189f85df3f49fbbeb847142ea20980.jpeg)