1. 二叉树的最近公共祖先
题目描述:

题解:
1.p或者q其中一个等于root,那么root就是最进公共祖先
2.p和q分布在root的左右两侧,那么root就是最进公共祖先
3.p和q在root的同一侧,就是要遍历这棵树,遇到p或者q返回
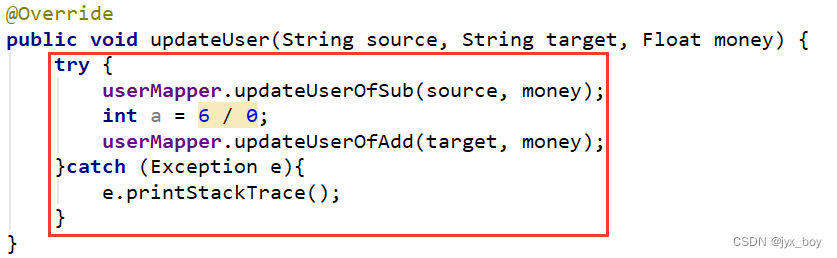
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null) {
return null;
}
//1.p或q在root的位置
if (p == root || q == root) {
return root;
}
TreeNode leftTree = lowestCommonAncestor(root.left, p, q);
TreeNode rightTree = lowestCommonAncestor(root.right, p, q);
//2.左边和右边都不空
if (leftTree != null && rightTree != null) {
return root;
} else if (leftTree != null) {
return leftTree; //3.左边不为空
} else {
return rightTree; //4。右边不为空
}
}第二种解法:
以链表思路求节解:就相当于求链表的交点
问题的关键就是如何存储,从根节点到p或者q的路径上的所有节点
//部分代码
//存储从根节点到p或者q路径上的所有节点
private boolean getPath(TreeNode root, TreeNode node, Stack<TreeNode> stack) {
if (root == null) {
return false;
}
stack.push(root);
if (root == node) {
return true;
}
boolean fag1 = getPath(root.left, node, stack);
if (fag1) {
return true;
}
boolean fag2 = getPath(root.right, node, stack);
if (fag2) {
return true;
}
stack.pop();
return false;
}2. 从前序与中序遍历序列构造二叉树
题目描述:
![]()
题解:
前序遍历(根 左 右)
大方向:遍历前序遍历数组,在中序遍历数组找到相对应的下标,左边是左树,右边是右树
2.找递归结束条件
下次下标ib肯定是大于ie的,所以,只要ib>ie,就结束了
public int preindex;
public TreeNode buildTree(int[] preorder, int[] inorder) {
return buildTreeChilde(preorder,inorder,0,inorder.length-1);
}
private TreeNode buildTreeChilde(int[] preorder,int[] inorder,int inBegin,int inEnd) {
if(inBegin > inEnd) {
return null; //没有左树 或者 右树
}
TreeNode root = new TreeNode(preorder[preindex]);
int rootIndex = findRootIndex(inorder,inBegin,inEnd,preorder[preindex]);
if(rootIndex == -1) {
return null;
}
preindex++;
root.left = buildTreeChilde(preorder,inorder,inBegin,rootIndex-1);
root.right = buildTreeChilde(preorder,inorder,rootIndex+1,inEnd);
return root;
}
private int findRootIndex(int[] inorder,int inBegin,int inEnd,int key) {
for(int i = inBegin; i <= inEnd; i++) {
if(inorder[i] == key) {
return i;
}
}
return -1;
}3.从中序与后序遍历序列构造二叉树
题目描述:
![]()
题解:
后序遍历(左 右 根)
1.遍历后序遍历,先创建的是右子树
2.遍历后序遍历下标是--
其它跟上题一致,稍微修改下代码
4.根据二叉树创建字符串
题目描述:


题解:
不怕大家笑话,开始的时候,读了题也没搞懂要做什么,一脸懵。也是看这示例明白的。
看这示例一:
1.根节点直接写
2.左边不为空&&右边为空
3.左边为空&&右边为空,什么都不做
示例二:
1.左边为空&&右边不为空,加一对括号
左边不为空与右边不为空,就是分别递归了!
private void tree2strChlide(TreeNode r, StringBuilder stringbuilder) {
if (r == null) {
return;
}
stringbuilder.append(r.val);
if (r.left != null) {
stringbuilder.append("(");
tree2strChlide(r.left, stringbuilder);
stringbuilder.append(")");
} else {
if (r.right == null) {
return;
} else {
stringbuilder.append("()");
}
}
//判断右树
if (r.right != null) {
stringbuilder.append("(");
tree2strChlide(r.right, stringbuilder);
stringbuilder.append(")");
} else {
return;
}
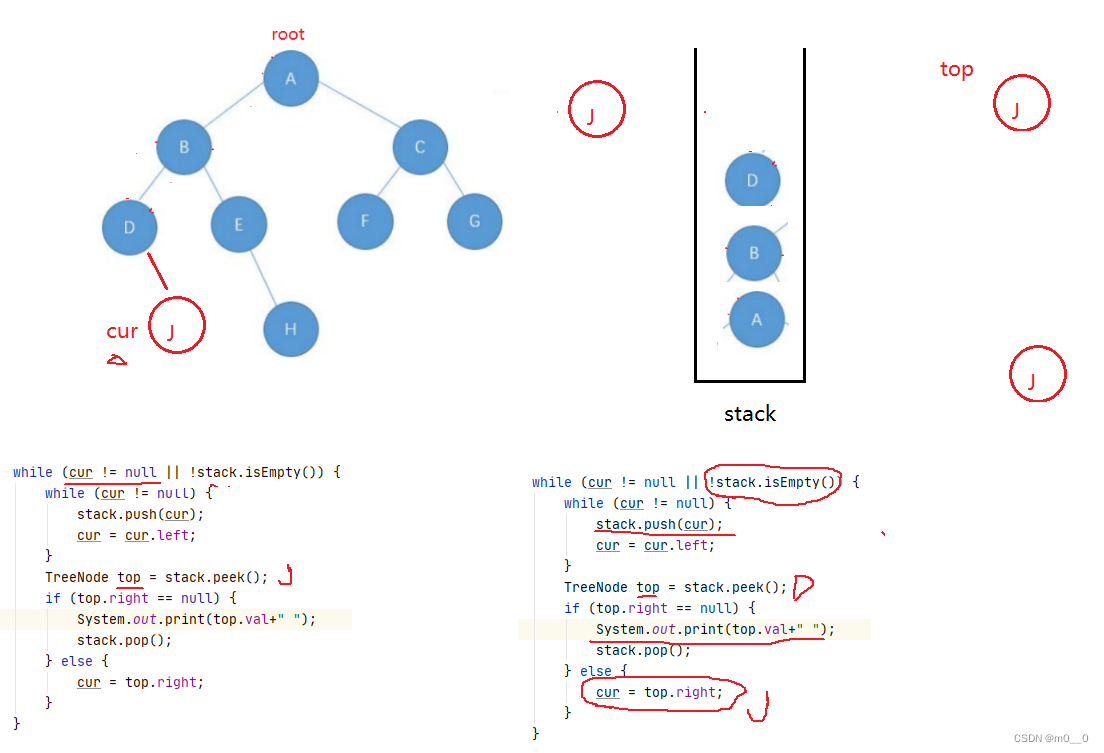
}5. 二叉树前序非递归遍历实现
题目描述:
![]()

题解:
非递归打印,最好还是引入栈来解决。
1.让cur指向root
2. 把cur放到栈中 打印 cur在指向左树
3.当cur == null 弹出栈顶元素并用top记录 让cur指向top的右树
关键是循环条件!

public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> ret = new ArrayList<>();
if (root == null) {
return ret;
}
TreeNode cur = root;
Stack<TreeNode> stack = new Stack<>();
while (cur != null || !stack.isEmpty()) {
while (cur != null) {
stack.push(cur);
//System.out.print(cur.val + " ");
ret.add(cur.val);
cur = cur.left;
}
TreeNode top = stack.pop();
cur = top.right;
}
return ret;
}5.1二叉树中序非递归遍历实现
题解:
5.2 二叉树后序非递归遍历实现

题解:
后序遍历(左 右 根)
首先,会有两种情况 cur != null或者 cur == null
1.cur != null,一直往左走
2.cur == null ,就不能在用pop(),要用peek(),判断右子树是否为null。
此时,会形成一个死循环!所以,打印这个top的时候,有两种情况。
1.右边 == null
2. 右边已经被打印完了(要记录一下)
public void posOrderNor(TreeNode root){
if(root == null) {
return;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
TreeNode prev = null;
while (cur != null || !stack.isEmpty()) {
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
TreeNode top = stack.peek();
if (top.right == null || top.right == prev) {
System.out.print(top.val+" ");
stack.pop();
prev = top;
} else {
cur = top.right;
}
}
}