在计算机科学与数学的交叉领域中，有一种特殊的整数被称为“水仙花数”，它是指一个三位数，其各位数字立方和等于该数本身。例如，153是一个典型的水仙花数，因为1³ + 5³ + 3³ = 1 + 125 + 27 = 153。

下面，我们通过一段C语言代码来深入解析如何找出100至999之间的所有水仙花数：

int main() {
    int i, a, b, c; // 定义整型变量i、a、b、c。其中i用于遍历100至999的所有数，a、b、c分别存储三位数的百位、十位和个位。

    for (i = 100; i <= 999; i++) { // 使用for循环逐个检查这个范围内的所有整数
        // 提取每位数字
        a = i / 100; // 利用整除运算获取百位数（整除结果自动舍去小数部分）
        b = (i / 10) % 10; // 先除以10得到前两位组成的数，再对10取余得到十位数
        c = i % 10; // 直接对10取余可得个位数
...

方法一：

// 计算每位数字的立方和
        // 方法一：直接进行乘法运算求立方
        if (a * a * a + b * b * b + c * c * c == i) {
            printf("%d 是水仙花数\n", i); // 如果满足条件，则输出该数为水仙花数
        }

方法二：

// 方法二：利用pow函数求立方
        // pow()是C语言标准库math.h中的内置函数，接受两个参数，返回第一个参数的第二个参数次方的结果
        if (pow(a, 3) + pow(b, 3) + pow(c, 3) == i) {
            printf("%d 也是水仙花数\n", i); // 使用pow函数验证并输出水仙花数
        }

        我们首先定义了变量i、a、b、c，然后使用for循环遍历100到999的所有整数。对于每个数i，我们采用不同的方式提取出它的各个位上的数字：通过整除和取余操作实现手动分离，以及通过调用pow()函数计算各位置上的数字的立方。

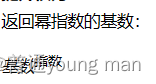
两种验证方法都完成了相同的任务——将三位数的每一位数字分别立方后求和，并判断这个立方和是否等于原数。尽管在这种特定场景下直接使用乘法运算更为简洁高效，但pow()函数展示了另一种通用且强大的数学运算能力，适用于更广泛的指数运算场景。

运行这段代码后，将会输出100到999之间所有的水仙花数，同时演示了两种有效的计算方法。

注：

pow函数：