时序预测 | Matlab实现GJO-VMD-LSTM金豺-变分模态分解-长短期记忆网络时间序列预测

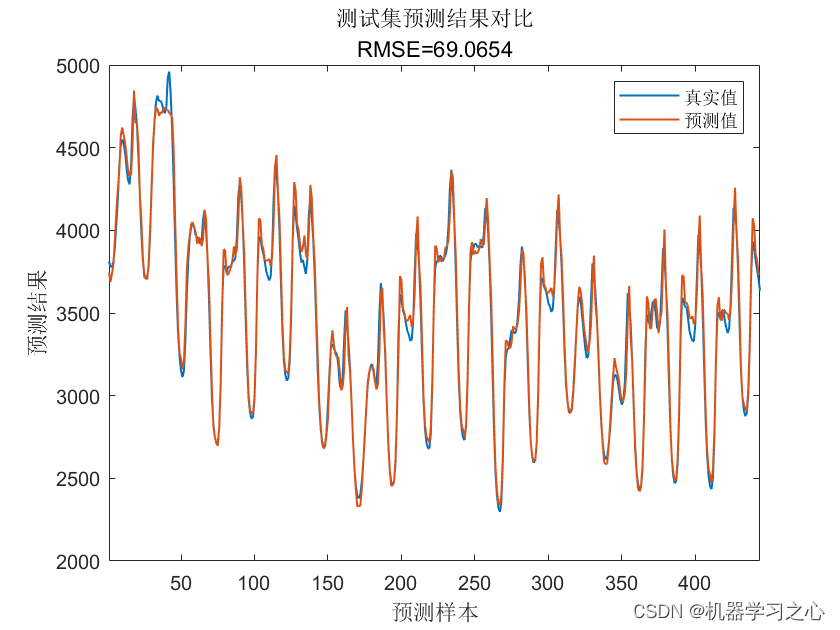
预测效果

基本介绍

Matlab实现GJO-VMD-LSTM金豺-变分模态分解-长短期记忆网络时间序列预测,GJO-VMD-LSTM（金豺-变分模态分解-长短期记忆网络）
GJO-VMD-LSTM是一个结合了金豺(Variational Mode Decomposition, VMD)和长短期记忆网络(LSTM)的时间序列预测方法。
VMD是一种信号分解方法，可以将时间序列分解成多个本征模态函数(Intrinsic Mode Functions, IMF)。每个IMF代表了原始时间序列中的一个特定频率成分。VMD能够将信号的时频特性分离开来，使得不同频率成分能够以不同的IMF表示。
GJO-VMD-LSTM将VMD和LSTM结合起来进行时间序列预测。首先，使用VMD将原始时间序列分解成多个IMF。然后，将每个IMF作为LSTM的输入序列，以便学习和预测每个IMF的未来值。最后，将所有IMF的预测结果相加，得到对原始时间序列的整体预测。
GJO-VMD-LSTM的优点在于能够考虑时间序列的时频特性，通过对不同频率成分进行分解和预测，可以更好地捕捉时间序列的多尺度变化。此外，LSTM网络能够学习和记忆时间序列的长期依赖关系，有助于提高预测的准确性。
主要用于时间序列预测
对比模型有lstm GJO-vmd-lstm GJO-vmd-GJO-lstm
通过GJO金豺优化算法对VMD进行参数寻优实现对预测数据进行分解，且同样采用GJO对LSTM进行参数寻优从而使模型达获得最优效果。
matlab代码，含有详细注释；
数据为excel数据，使用时替换数据集即可；
matlab代码，含有详细注释；

模型设计

数据准备：收集并整理待预测的时间序列数据。确保数据是按照时间顺序排列的。

变分模态分解（VMD）：使用VMD将原始时间序列分解成多个本征模态函数（IMF）。VMD的步骤如下：

a. 设定VMD的参数，如分解层数、正则化参数等。

b. 将原始时间序列输入VMD模型，进行分解。VMD会输出每个IMF以及一个残差项（通常是高频成分）。

数据预处理：对每个IMF进行数据预处理，以便作为LSTM的输入。预处理步骤通常包括归一化、平滑、去除趋势等。

构建训练集和测试集：将预处理后的每个IMF划分为训练集和测试集。通常，较早的数据用作训练集，较新的数据用作测试集。

LSTM模型训练：使用训练集数据训练LSTM模型。LSTM模型可以采用标准的LSTM结构或者其他改进的变体，具体结构根据实际情况进行选择。

LSTM模型预测：使用训练好的LSTM模型对测试集进行预测。将每个IMF的测试集输入LSTM模型，得到对应的预测结果。

IMF重构：将每个IMF的预测结果合并，得到整体的时间序列预测结果。可以将每个IMF的预测结果相加或者按照一定权重进行叠加。

评估和调优：使用适当的评估指标（如均方根误差、平均绝对误差等）评估预测结果的准确性。根据需要，可以对模型进行调优，如调整参数、改变模型结构等。

时间序列预测：使用训练好的GJO-VMD-LSTM模型对未来的时间序列进行预测。将新的时间步输入模型，得到相应的预测结果。

程序设计

• 完整源码和数据获取方式：私信博主回复Matlab实现GJO-VMD-LSTM金豺-变分模态分解-长短期记忆网络时间序列预测。

%%  获取最优种群
   for j = 1 : SearchAgents
       if(fitness_new(j) < GBestF)
          GBestF = fitness_new(j);
          GBestX = X_new(j, :);
       end
   end
   
%%  更新种群和适应度值
   pop_new = X_new;
   fitness = fitness_new;

%%  更新种群 
   [fitness, index] = sort(fitness);
   for j = 1 : SearchAgents
      pop_new(j, :) = pop_new(index(j), :);
   end

%%  得到优化曲线
   curve(i) = GBestF;
   avcurve(i) = sum(curve) / length(curve);
end

%%  得到最优值
Best_pos = GBestX;
Best_score = curve(end);

%%  得到最优参数
NumOfUnits       =abs(round( Best_pos(1,3)));       % 最佳神经元个数
InitialLearnRate =  Best_pos(1,2) ;% 最佳初始学习率
L2Regularization = Best_pos(1,1); % 最佳L2正则化系数
% 
inputSize = k;
outputSize = 1;  %数据输出y的维度  
%  参数设置
opts = trainingOptions('adam', ...                    % 优化算法Adam
    'MaxEpochs', 20, ...                              % 最大训练次数
    'GradientThreshold', 1, ...                       % 梯度阈值
    'InitialLearnRate', InitialLearnRate, ...         % 初始学习率
    'LearnRateSchedule', 'piecewise', ...             % 学习率调整
    'LearnRateDropPeriod', 6, ...                     % 训练次后开始调整学习率
    'LearnRateDropFactor',0.2, ...                    % 学习率调整因子
    'L2Regularization', L2Regularization, ...         % 正则化参数
    'ExecutionEnvironment', 'gpu',...                 % 训练环境
    'Verbose', 0, ...                                 % 关闭优化过程
    'SequenceLength',1,...
    'MiniBatchSize',10,...
    'Plots', 'training-progress');                    % 画出曲线

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/128577926?spm=1001.2014.3001.5501
[2] https://blog.csdn.net/kjm13182345320/article/details/128573597?spm=1001.2014.3001.5501