文章目录
- 概览:RL方法分类
- 时序差分学习(Temporal Difference,TD)
- TD for state values
- 🟦Basic TD
- 🟡TD vs. MC
- 🟦Sarsa (TD for action values)
- Basic Sarsa
- 变体1:Expected Sarsa
- 变体2:n-step Sarsa
- 🟦Q-learing (TD for optimal action values)
- 🟡TD算法汇总
- *随机近似(SA)&随机梯度下降(SGD)
- Robbins-Monro(RM)算法
- 随机梯度下降(Stochastic Gradient Descent,SGD)
- BGD / MBGD / SGD
本系列文章介绍强化学习基础知识与经典算法原理,大部分内容来自西湖大学赵世钰老师的强化学习的数学原理课程(参考资料1),并参考了部分参考资料2、3的内容进行补充。
系列博文索引:
- 强化学习的数学原理学习笔记 - RL基础知识
- 强化学习的数学原理学习笔记 - 基于模型(Model-based)
- 强化学习的数学原理学习笔记 - 蒙特卡洛方法(Monte Carlo)
- 强化学习的数学原理学习笔记 - 时序差分学习(Temporal Difference)
- 强化学习的数学原理学习笔记 - 值函数近似(Value Function Approximation)
- 强化学习的数学原理学习笔记 - 策略梯度(Policy Gradient)
- 强化学习的数学原理学习笔记 - Actor-Critic
参考资料:
- 【强化学习的数学原理】课程:从零开始到透彻理解(完结)(主要)
- Sutton & Barto Book: Reinforcement Learning: An Introduction
- 机器学习笔记
*注:【】内文字为个人想法,不一定准确
概览:RL方法分类
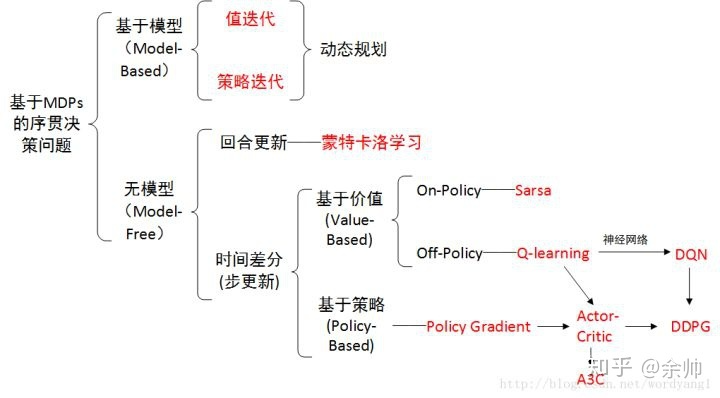
*图源:https://zhuanlan.zhihu.com/p/36494307
时序差分学习(Temporal Difference,TD)
先前的内容介绍了如何在无模型(model-free)的情况下,基于蒙特卡洛方法(Monte Carlo,MC)来进行策略评估。实际上,无模型的强化学习方法还有另外一个重要分支:时序差分学习(Temporal Difference,TD)。
最基础的时序差分学习估计状态值,而后续提出的Sarsa和Q-learning方法则直接对动作值进行估计。
*注:时序差分的原理部分依赖于随机优化理论,可参阅本文后续的随机近似(SA)&随机梯度下降(SGD)章节。
TD for state values
🟦Basic TD
最原始的TD Learning算法:在策略评估中估计给定策略 π \pi π的状态值 v π v_\pi vπ,本质上是在无模型的情况下求解贝尔曼方程(解法类似于RM算法,详见后一章节)。
-
v
t
+
1
(
s
t
)
=
v
t
(
s
t
)
−
α
(
s
t
)
[
v
t
(
s
t
)
−
[
r
t
+
1
+
γ
v
t
(
s
t
+
1
)
]
]
v_{t+1}(s_t) = v_t(s_t) - \alpha(s_t) [v_t (s_t) - [r_{t+1} + \gamma v_t(s_{t+1})] ]
vt+1(st)=vt(st)−α(st)[vt(st)−[rt+1+γvt(st+1)]]
- * α t ( s t ) \alpha_t (s_t) αt(st)是学习率,通常设为很小的常数
- v t + 1 ( s ) = v t ( s ) , ∀ s ≠ s t v_{t+1} (s) = v_t (s), \quad \forall s \neq s_t vt+1(s)=vt(s),∀s=st
在 t = 0 , 1 , 2 , ⋯ t =0, 1,2, \cdots t=0,1,2,⋯时刻,更新被访问状态 s t s_t st的状态值估计 v t + 1 ( s t ) v_{t+1}(s_t) vt+1(st),但不更新其他未访问状态的状态值估计。
TD的目标:使得估计值
v
t
(
s
t
)
v_{t}(s_t)
vt(st)接近
v
ˉ
t
\bar{v}_t
vˉt(*对于估计动作值的TD算法而言,是使得
q
t
(
s
t
,
a
t
)
q_t(s_t, a_t)
qt(st,at)接近于
q
ˉ
t
\bar{q}_t
qˉt
v
t
+
1
(
s
t
)
⏟
new estimation
=
v
t
(
s
t
)
⏟
current estimation
−
α
(
s
t
)
[
v
t
(
s
t
)
−
[
r
t
+
1
+
γ
v
t
(
s
t
+
1
)
⏟
TD target
v
ˉ
t
]
⏞
TD error
δ
t
]
\underbrace{v_{t+1}(s_t)}_{\text{new estimation}} = \underbrace{v_t(s_t)}_{\text{current estimation}} - \alpha(s_t) [\overbrace{v_t (s_t) - [\underbrace{r_{t+1} + \gamma v_t(s_{t+1})}_{\text{TD target } \bar{v}_t}]}^{\text{TD error } \delta_t} ]
new estimation
vt+1(st)=current estimation
vt(st)−α(st)[vt(st)−[TD target vˉt
rt+1+γvt(st+1)]
TD error δt]
- TD target: v ˉ t = r t + 1 + γ v t ( s t + 1 ) \bar{v}_t = r_{t+1} + \gamma v_t(s_{t+1}) vˉt=rt+1+γvt(st+1)
- TD error:
δ
t
=
v
t
(
s
t
)
−
[
r
t
+
1
+
γ
v
t
(
s
t
+
1
)
]
=
v
t
(
s
t
)
−
v
ˉ
t
\delta_t = v_t (s_t) - [r_{t+1} + \gamma v_t(s_{t+1})] = v_{t}(s_t) - \bar{v}_t
δt=vt(st)−[rt+1+γvt(st+1)]=vt(st)−vˉt
- 是 t t t和 t + 1 t+1 t+1两个时刻的difference
- 描述了 v t v_t vt与 v π v_\pi vπ之间的差异( v t v_t vt是对 v π v_\pi vπ的估计):若 v t = v π v_t = v_\pi vt=vπ,则 δ t = 0 \delta_t = 0 δt=0
这种最原始的TD算法不能用来估计动作值,也不能用来搜索最优策略。
*注:不同文献和资料中的公式表述存在差异,比如Sutton书中(参考资料2)的TD形式如下:
V
(
S
t
)
←
V
(
S
t
)
+
α
[
R
t
+
1
+
γ
V
(
S
t
+
1
)
−
V
(
S
t
)
]
V(S_t) \larr V(S_t) + \alpha [R_{t+1} + \gamma V(S_{t+1}) - V(S_t)]
V(St)←V(St)+α[Rt+1+γV(St+1)−V(St)]
TD算法本质上是求解贝尔曼期望方程(Bellman Expectation Equation):
v
π
(
s
)
=
E
[
R
+
γ
v
π
(
S
′
)
∣
S
=
s
]
,
s
∈
S
v_\pi(s) = \mathbb{E} [R + \gamma v_\pi (S') | S = s], \quad s \in S
vπ(s)=E[R+γvπ(S′)∣S=s],s∈S
TD算法的收敛性:如满足以下条件,则当
t
→
∞
t\rarr\infin
t→∞时,
v
t
(
s
)
v_t(s)
vt(s)可以收敛至
v
π
(
s
)
v_\pi(s)
vπ(s)(w.p.1,
∀
s
∈
S
\forall s \in \mathcal{S}
∀s∈S)
∀
s
∈
S
\forall s \in \mathcal{S}
∀s∈S,
∑
t
a
t
(
s
)
=
∞
\textstyle\sum_{t} a_t(s) = \infin
∑tat(s)=∞且
∑
t
a
t
2
(
s
)
<
∞
\textstyle\sum_{t} a_t^2(s) < \infin
∑tat2(s)<∞
*需要对每个状态访问很多次(理论上是无穷次)
🟡TD vs. MC
| TD / Sarsa | MC |
|---|---|
| Online:可以使用每步的reward,立即更新状态/动作值 | Offline:需要等待每个episode数据采集完毕 |
| Continuing & Episodic tasks | 仅Episodic tasks |
| Bootstrapping:依赖于初始估计和历史估计 | Non-bootstrapping:直接估计,不依赖初始值 |
| Lower estimation variance:只依赖少数几个随机变量 | Higher estimation variance:依赖的随机变量较多 |
TD估计的期望是有偏的,因为其依赖于初始估计(Bootstrapping),但随着数据量的增加,最终会收敛到正确的估计值;相反,MC的期望是无偏估计。
🟦Sarsa (TD for action values)
Basic Sarsa
目标:估计给定策略
π
\pi
π的动作值
q
π
(
s
,
a
)
q_\pi(s, a)
qπ(s,a)
数据:
{
(
s
t
,
a
t
,
r
t
+
1
,
s
t
+
1
,
a
t
+
1
)
}
\{(s_t, a_t, r_{t+1}, s_{t+1}, a_{t+1})\}
{(st,at,rt+1,st+1,at+1)}
SARSA(State-Action-Reward-State-Action) 算法:
- q t + 1 ( s t , a t ) = q t ( s t , a t ) − α t ( s t , a t ) [ q t ( s t , a t ) − [ r t + 1 + γ q t ( s t + 1 , a t + 1 ) ] ] q_{t+1} (s_{t}, a_t) = q_{t} (s_{t}, a_t) - \alpha_t (s_t, a_t) [q_{t} (s_t, a_t) - [r_{t+1} + \gamma {\color{red} q_t (s_{t+1}, a_{t+1})}]] qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−[rt+1+γqt(st+1,at+1)]]
-
q
t
+
1
(
s
,
a
)
=
q
t
(
s
,
a
)
,
∀
(
s
,
a
)
≠
(
s
t
,
a
t
)
q_{t+1} (s, a) = q_t (s, a), \quad \forall (s, a) \neq (s_t, a_t)
qt+1(s,a)=qt(s,a),∀(s,a)=(st,at)
- α t ( s t , a t ) \alpha_t (s_t, a_t) αt(st,at)是取决于 s t s_t st和 a t a_t at的学习率
*与原始TD算法的差异:将公式中的 v ( s t ) v(s_t) v(st)替换为 q ( s t , a t ) q(s_t, a_t) q(st,at),因此Sarsa是TD算法的动作值估计的版本
Sarsa求解贝尔曼期望方程的动作值形式:
q
π
(
s
,
a
)
=
E
[
R
+
γ
q
π
(
S
′
,
A
′
)
∣
s
,
a
]
,
∀
s
,
a
q_\pi(s, a) = \mathbb{E} [R + \gamma q_\pi (S', A') | s, a], \quad \forall s, a
qπ(s,a)=E[R+γqπ(S′,A′)∣s,a],∀s,a
其中,
R
∼
p
(
R
∣
s
,
a
)
R \sim p (R | s ,a)
R∼p(R∣s,a),
S
′
∼
p
(
S
′
∣
s
,
a
)
S' \sim p(S' | s, a)
S′∼p(S′∣s,a),
A
′
∼
π
(
A
′
∣
S
′
)
A' \sim \pi(A' | S')
A′∼π(A′∣S′)(
∼
\sim
∼表示服从某种概率分布)。
注意到Sarsa所依赖的5个变量中,在给定 s t s_t st和 a t a_t at的情况下,只有 a t + 1 a_{t+1} at+1依赖于策略 π t \pi_t πt,而 r t + 1 r_{t+1} rt+1和 s t + 1 s_{t+1} st+1本身并不依赖于策略,而是依赖于转移概率分布(通过采样确定)。
Sarsa收敛性类似于TD,略。
Sarsa+策略提升的完整算法:(也属于GPI框架)
- 更新动作值(策略评估):Sarsa的公式,略
- 更新策略(策略提升):ε-Greedy方法,基于
q
t
+
1
(
s
t
,
a
)
q_{t+1} (s_t, a)
qt+1(st,a)立即更新
- π k + 1 ( a ∣ s t ) = { 1 − ε ∣ A ∣ ( ∣ A ∣ − 1 ) if a = arg max a q t + 1 ( s t , a ) ε ∣ A ∣ otherwise \pi_{k+1}(a|s_t) = \begin{cases} 1-\frac{\varepsilon}{|\mathcal{A}|} (|\mathcal{A}|-1) &\text{if } a = \argmax_a q_{t+1}(s_t, a) \\ \frac{\varepsilon}{|\mathcal{A}|} &\text{otherwise} \end{cases} πk+1(a∣st)={1−∣A∣ε(∣A∣−1)∣A∣εif a=argmaxaqt+1(st,a)otherwise
Sarsa有两个变体:Expected Sarsa和n-step Sarsa
变体1:Expected Sarsa
- q t + 1 ( s t , a t ) = q t ( s t , a t ) − α t ( s t , a t ) [ q t ( s t , a t ) − [ r t + 1 + γ E q t ( s t + 1 , A ) ] ] q_{t+1} (s_{t}, a_t) = q_{t} (s_{t}, a_t) - \alpha_t (s_t, a_t) [q_{t} (s_t, a_t) - [r_{t+1} + \gamma {\color{red} \mathbb{E} q_t (s_{t+1}, A)}]] qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−[rt+1+γEqt(st+1,A)]]
- q t + 1 ( s , a ) = q t ( s , a ) , ∀ ( s , a ) ≠ ( s t , a t ) q_{t+1} (s, a) = q_t (s, a), \quad \forall (s, a) \neq (s_t, a_t) qt+1(s,a)=qt(s,a),∀(s,a)=(st,at)
其中, E q t ( s t + 1 , A ) = v t ( s t + 1 ) \mathbb{E} q_t (s_{t+1}, A) = v_t (s_{t + 1}) Eqt(st+1,A)=vt(st+1)是状态值而非动作值
Expected Sarsa求解以下形式的贝尔曼公式:
q
π
(
s
,
a
)
=
E
[
R
t
+
1
+
γ
v
π
(
S
t
+
1
)
∣
S
t
=
s
,
A
t
=
a
]
q_\pi (s, a) = \mathbb{E} [R_{t+1} + \gamma v_\pi(S_{t+1}) | S_t =s, A_t =a]
qπ(s,a)=E[Rt+1+γvπ(St+1)∣St=s,At=a]
与Sarsa的区别:
- 改变了TD Target
- 需要更多的计算量,但减少了随机变量个数(不需要对 a t + 1 a_{t+1} at+1采样),随机性减少
变体2:n-step Sarsa
n-step Sarsa是Sarsa的推广,统一了Sarsa和MC的思想
- Sarsa基于单步采样进行估计,MC基于∞步采样进行估计,因此n-step Sarsa相当于是二者的折中
- n-step Sarsa既不是online的,也不是offline的(或者是是特殊的online方法)

公式及其他细节略。
n-step Sarsa本身仅用于策略估计,也可以和策略提升相结合。
🟦Q-learing (TD for optimal action values)
Q-learing直接估计最优动作值,因此不需要策略评估-策略提升的过程。
- q t + 1 ( s t , a t ) = q t ( s t , a t ) − α t ( s t , a t ) [ q t ( s t , a t ) − [ r t + 1 + γ max a ∈ A q t ( s t + 1 , a ) ] ] q_{t+1} (s_{t}, a_t) = q_{t} (s_{t}, a_t) - \alpha_t (s_t, a_t) [q_{t} (s_t, a_t) - [r_{t+1} + \gamma {\color{red} \max_{a \in \mathcal{A}} q_t (s_{t+1}, a)}]] qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−[rt+1+γmaxa∈Aqt(st+1,a)]]
- q t + 1 ( s , a ) = q t ( s , a ) , ∀ ( s , a ) ≠ ( s t , a t ) q_{t+1} (s, a) = q_t (s, a), \quad \forall (s, a) \neq (s_t, a_t) qt+1(s,a)=qt(s,a),∀(s,a)=(st,at)
Q-learing和Sarsa在公式上的唯一区别是TD target(公式的红字部分)。每个状态下,Q-learing在对action进行优化,但Sarsa只是依据当前策略选择action。
Sarsa求解贝尔曼方程,但Q-learing求解贝尔曼最优方程:
q
(
s
,
a
)
=
E
[
R
t
+
1
+
γ
max
a
q
(
s
t
+
1
,
a
)
∣
S
t
=
s
,
A
t
=
a
]
,
∀
s
,
a
q(s, a) = \mathbb{E} [ R_{t+1} + \gamma \max_a q(s_{t+1}, a) | S_t =s, A_t = a ], \quad \forall s,a
q(s,a)=E[Rt+1+γmaxaq(st+1,a)∣St=s,At=a],∀s,a
此外,Sarsa属于on-policy算法,而Q-learing属于off-policy算法。
- Sarsa所需的 a t + 1 a_{t+1} at+1依赖于 π t \pi_t πt,之后根据动作值估计来更新策略为 π t + 1 \pi_{t+1} πt+1,可见其行为策略与目标策略相同
- Q-learing所需的数据为
{
(
s
t
,
a
t
,
r
t
+
1
,
s
t
+
1
)
}
\{(s_t, a_t, r_{t+1}, s_{t+1})\}
{(st,at,rt+1,st+1)},这4个变量都不依赖于特定策略(或者说可以由任意策略生成),因此其行为策略与目标策略可以不同
- *二者相同时,Q-learing即为on-policy
Q-learing算法步骤(off-policy):
由行为策略
π
B
\pi_B
πB生成若干episode,每个episode包含
{
s
0
,
a
0
,
r
1
,
s
1
,
a
1
,
r
2
,
⋯
}
\{ s_0, a_0, r_1, s_1, a_1, r_2, \cdots \}
{s0,a0,r1,s1,a1,r2,⋯}。
- *例子: π B \pi_B πB可以取 ε = 1 \varepsilon =1 ε=1的ε-Greedy,保证对每个动作等概率探索
在每个episode的每个时间步 t = 0 , 1 , 2 , ⋯ t=0,1,2,\cdots t=0,1,2,⋯中:
- 更新最优动作值(q-value)的估计:Q-learing的公式,略
- 更新目标策略
π
T
\pi_T
πT:
π
T
,
t
+
1
=
{
1
if
a
=
arg max
a
q
t
+
1
(
s
t
,
a
)
0
otherwise
\pi_{T, t+1} = \begin{cases} 1 &\text{if } a = \argmax_a q_{t+1} (s_t, a) \\ 0 &\text{otherwise} \end{cases}
πT,t+1={10if a=argmaxaqt+1(st,a)otherwise
- 是greedy,但不是ε-greedy(不需要探索)
对于off-policy的Q-learing而言,行为策略的探索性越强,其目标策略收敛于最优策略的速度越快。
🟡TD算法汇总
所有估计动作值的TD算法可以由下式统一表示:
q
t
+
1
(
s
t
,
a
t
)
=
q
t
(
s
t
,
a
t
)
−
α
t
(
s
t
,
a
t
)
[
q
t
(
s
t
,
a
t
)
−
q
ˉ
t
]
q_{t+1} (s_{t}, a_t) = q_{t} (s_{t}, a_t) - \alpha_t (s_t, a_t) [q_{t} (s_t, a_t) - {\color{blue} \bar{q}_t}]
qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−qˉt]
其中,
q
ˉ
t
\bar{q}_t
qˉt为TD target,而TD算法的目标即使得
q
t
(
s
t
,
a
t
)
q_t(s_t,a_t)
qt(st,at)接近
q
ˉ
t
\bar{q}_t
qˉt,或者说缩小TD error(
q
t
(
s
t
,
a
t
)
−
q
ˉ
t
q_{t} (s_t, a_t) - {\bar{q}_t}
qt(st,at)−qˉt)。
不同算法的差异在于 q ˉ t \bar{q}_t qˉt的形式不同:【注意到,TD和MC实际上是有关联的,主要差异是采样的数量不同】
| 算法 | q ˉ t \bar{q}_t qˉt形式 |
|---|---|
| Sarsa | q ˉ t = r t + 1 + γ q t ( s t + 1 , a t + 1 ) \bar{q}_t = r_{t+1} + \gamma q_{t} (s_{t+1}, a_{t+1}) qˉt=rt+1+γqt(st+1,at+1) |
| Expected-Sarsa | q ˉ t = r t + 1 + γ ∑ a π t ( a ∣ s t + 1 ) q t ( s t + 1 , a ) \bar{q}_t = r_{t+1} + \gamma \textstyle\sum_a\pi_t(a|s_{t+1}) q_{t} (s_{t+1}, a) qˉt=rt+1+γ∑aπt(a∣st+1)qt(st+1,a) |
| n-step Sarsa | q ˉ t = r t + 1 + γ r t + 2 + ⋯ + γ n q t ( s t + n , a t + n ) \bar{q}_t = r_{t+1} + \gamma r_{t+2} + \cdots + \gamma^{n} q_{t} (s_{t+n}, a_{t+n}) qˉt=rt+1+γrt+2+⋯+γnqt(st+n,at+n) |
| Q-learning | q ˉ t = r t + 1 + γ max a q t ( s t + 1 , a ) \bar{q}_t = r_{t+1} + \gamma \textstyle\max_a q_{t} (s_{t+1}, a) qˉt=rt+1+γmaxaqt(st+1,a) |
| Monte Carlo | q ˉ t = r t + 1 + γ r t + 2 + ⋯ + γ ∞ r t + ∞ \bar{q}_t = r_{t+1} + \gamma r_{t+2} + \cdots + \gamma^{\infin} r_{t+\infin} qˉt=rt+1+γrt+2+⋯+γ∞rt+∞(均为单步折扣奖励,没有 q t q_t qt) |
不同算法求解的公式也不同:

*随机近似(SA)&随机梯度下降(SGD)
【*注:本节内容主要是为理解时序差分的原理提供资料,但与强化学习核心内容关系不大,可以跳过。】
考虑求解均值估计(Mean Estimation)问题,MC利用采样的算数均值来估计期望,但缺点是需要等待所有样本收集完毕后再进行计算。
另一种求解思路:用增量和迭代方法进行计算,有多少数据利用多少数据。
举例:如何增量和迭代式地计算均值?
设
w
k
+
1
=
1
k
∑
i
=
1
k
x
i
w_{k+1} = \frac{1}{k} \sum_{i=1}^{k} x_i
wk+1=k1∑i=1kxi,可知
w
k
+
1
=
w
k
−
1
k
(
w
k
−
x
k
)
w_{k+1} = w_k - \frac{1}{k} (w_k - x_k)
wk+1=wk−k1(wk−xk)。基于该方式,只需要基于过去的均值计算结果
w
k
w_k
wk和新采样
x
k
x_k
xk,即可计算出总体均值【思路上有点像是EWMA】。采样数量越多,计算结果越准确。
可以对上式进一步推广,得到 w k + 1 = w k − α k ( w k − x k ) w_{k+1} = w_k - {\color{red}\alpha_k} (w_k - x_k) wk+1=wk−αk(wk−xk),其中 α k > 0 \alpha_k>0 αk>0。可以证明,当 α k \alpha_k αk满足一定条件时,其迭代的计算结果会收敛至期望值。这是一种特殊的随机近似(SA)/随机梯度下降(SGD)算法。
随机近似(Stochastic Approximation,SA):一类随机迭代算法,适用于方程求解或优化问题,但不需要目标函数/方程的表达式/导数形式。
Robbins-Monro(RM)算法
目标:在不知道
g
(
w
)
g(w)
g(w)的具体形式的情况下(视作黑盒),求解
g
(
w
)
=
0
g(w) = 0
g(w)=0,设其解为
w
∗
w^*
w∗。
*
g
(
w
)
g(w)
g(w)须为单调递增
RM算法:
w
k
+
1
=
w
k
−
a
k
g
~
(
w
k
,
η
k
)
w_{k+1} = w_k - a_k \tilde{g} (w_k, \eta_k)
wk+1=wk−akg~(wk,ηk)
- w k w_k wk:对 w ∗ w^* w∗的第 k k k次估计
- g ~ ( w k , η k ) = g ( w k ) + η k \tilde{g} (w_k, \eta_k) = g(w_k) + \eta_k g~(wk,ηk)=g(wk)+ηk,其中 η k \eta_k ηk是噪声,因此 g ~ \tilde{g} g~表示对 g g g的带有噪声的观测
- a k > 0 a_k>0 ak>0:系数
RM算法依赖于数据:
- 输入序列: { w k } \{w_k\} {wk}
- 带噪声的输出序列: { g ~ ( w k , η k ) } \{\tilde{g} (w_k, \eta_k)\} {g~(wk,ηk)}
RM定理(收敛性):在RM算法中,当以下三个条件成立时, w k w_k wk会按照概率1(w.p.1)收敛至 w ∗ w^* w∗
-
g
(
w
)
g(w)
g(w)的梯度需满足:
0
<
c
1
≤
∇
w
g
(
w
)
≤
c
2
,
∀
w
0 < c_1 \leq \nabla_{w} g(w) \leq c_2, \quad\forall w
0<c1≤∇wg(w)≤c2,∀w
- g g g须为单调递增,以保证 g ( w ) = 0 g(w)=0 g(w)=0的解存在且唯一
- g g g的梯度(对于多元函数,导数沿梯度方向取最大值)须有上界,以避免函数发散
-
a
k
a_k
ak需满足:
∑
k
=
1
∞
a
k
=
∞
\textstyle\sum_{k=1}^{\infin} a_k = \infin
∑k=1∞ak=∞且
∑
k
=
1
∞
a
k
2
<
∞
\textstyle\sum_{k=1}^{\infin} a_k^2 < \infin
∑k=1∞ak2<∞
- 平方和小于无穷:随着 k → ∞ k\rarr\infin k→∞, a k a_k ak收敛至0
- 和等于无穷: a k a_k ak收敛至0的速度不能太快
-
η
k
\eta_k
ηk需满足:
E
[
η
k
∣
H
k
]
=
0
\mathbb{E} [\eta_k | \mathcal{H}_k] = 0
E[ηk∣Hk]=0且
E
[
η
k
2
∣
H
k
]
<
∞
\mathbb{E} [\eta_k^2 | \mathcal{H}_k] < \infin
E[ηk2∣Hk]<∞
- η k \eta_k ηk的均值为0且方差有界
- 常见情形: { η k } \{\eta_k\} {ηk}为独立同分布随机序列(但不要求是正态分布)
a k a_k ak的常见选择: a k = 1 k a_k = \frac{1}{k} ak=k1(或非常小的常数,为了避免最近采样的权重下降)
- ∑ k = 1 ∞ a k = ∞ \textstyle\sum_{k=1}^{\infin} a_k = \infin ∑k=1∞ak=∞
欧拉常数(Euler-Mascheroni constant)
γ = lim n → ∞ ( ∑ k = 1 n 1 k − ln n ) ≈ 0.557 \gamma = \lim_{n\rarr\infin} (\sum_{k=1}^{n}\frac{1}{k} - \ln n) \approx 0.557 γ=limn→∞(∑k=1nk1−lnn)≈0.557
当 n → ∞ n\rarr\infin n→∞时, ln n → ∞ \ln n\rarr\infin lnn→∞,因此可知 ∑ k = 1 ∞ 1 k = ∞ \sum_{k=1}^{\infin}\frac{1}{k} = \infin ∑k=1∞k1=∞
- ∑ k = 1 ∞ a k 2 < ∞ \textstyle\sum_{k=1}^{\infin} a_k^2 < \infin ∑k=1∞ak2<∞
巴塞尔问题(Basel Problem)
∑ k = 1 ∞ 1 k 2 = π 2 6 < ∞ \sum_{k=1}^{\infin}\frac{1}{k^2} = \frac{\pi^2}{6} < \infin ∑k=1∞k21=6π2<∞
随机梯度下降(Stochastic Gradient Descent,SGD)
SGD是RM算法的一种特殊情况。
目标:求解以下优化问题
min
w
J
(
w
)
=
E
[
f
(
w
,
X
)
]
\min_w \quad J(w) = \mathbb{E} [f(w, X)]
wminJ(w)=E[f(w,X)]
- w w w:待优化参数
- X X X:随机变量, E \mathbb{E} E是关于 X X X的期望
- w w w与 X X X可以是标量或向量,函数 f ( ⋅ ) f(\cdot) f(⋅)为标量
*最小化用梯度下降,最大化用梯度上升
求解方法1:GD
w
k
+
1
=
w
k
−
α
k
∇
w
E
[
f
(
w
k
,
X
)
]
=
w
k
−
α
k
E
[
∇
w
f
(
w
k
,
X
)
]
w_{k+1} = w_k - \alpha_k \nabla_w \mathbb{E}[f(w_k, X)] = w_k - \alpha_k \mathbb{E}[\nabla_w f(w_k, X)]
wk+1=wk−αk∇wE[f(wk,X)]=wk−αkE[∇wf(wk,X)]
- 缺陷:期望难以直接计算
求解方法2:BGD(Batch Gradient Descent),基于数据采样计算期望
E
[
∇
w
f
(
w
k
,
X
)
]
≈
1
n
∑
i
=
1
n
∇
w
f
(
w
k
,
x
i
)
\mathbb{E}[\nabla_w f(w_k, X)] \approx \frac{1}{n} \sum_{i=1}^{n} \nabla_w f(w_k, x_i)
E[∇wf(wk,X)]≈n1∑i=1n∇wf(wk,xi)(
n
n
n次采样)
w
k
+
1
=
w
k
−
α
k
1
n
∑
i
=
1
n
∇
w
f
(
w
k
,
x
i
)
w_{k+1} = w_k - \alpha_k \frac{1}{n} \sum_{i=1}^{n} \nabla_w f(w_k, x_i)
wk+1=wk−αkn1∑i=1n∇wf(wk,xi)
- 缺陷: w k w_k wk的每次迭代都需要很多采样
求解方法3:SGD
w
k
+
1
=
w
k
−
α
k
∇
w
f
(
w
k
,
x
k
)
w_{k+1} = w_k - \alpha_k \nabla_w f(w_k, x_k)
wk+1=wk−αk∇wf(wk,xk)
- 与GD的差异:将真实梯度(true gradient) E [ ∇ w f ( w k , X ) ] \mathbb{E}[\nabla_w f(w_k, X)] E[∇wf(wk,X)]替换为随机梯度(stochastic gradient) ∇ w f ( w k , x k ) \nabla_w f(w_k, x_k) ∇wf(wk,xk)
- 与BGD的差异:仅采样一次( n = 1 n=1 n=1)
SGD收敛性:若以下三个条件成立,则 w k w_k wk会按照概率1(w.p.1)收敛至 w ∗ w^* w∗( ∇ w E [ f ( w , X ) ] = 0 \nabla_w \mathbb{E} [f(w, X)] = 0 ∇wE[f(w,X)]=0的解)
-
0
<
c
1
≤
∇
w
2
f
(
w
,
X
)
≤
c
2
0 < c_1 \leq \nabla_{w}^2 f(w, X) \leq c_2
0<c1≤∇w2f(w,X)≤c2(二阶梯度)
- f ( ⋅ ) f(\cdot) f(⋅)是严格凸函数(标量)
- ∑ k = 1 ∞ a k = ∞ \textstyle\sum_{k=1}^{\infin} a_k = \infin ∑k=1∞ak=∞且 ∑ k = 1 ∞ a k 2 < ∞ \textstyle\sum_{k=1}^{\infin} a_k^2 < \infin ∑k=1∞ak2<∞
- { x k } k = 1 ∞ \{x_k\}_{k=1}^{\infin} {xk}k=1∞为独立同分布(i.i.d)
SGD的收敛模式:
- 当 w k w_k wk距离 w ∗ w^* w∗较远时,SGD的表现与GD相似,即 w k w_k wk随着迭代不断向 w ∗ w^* w∗逼近
- 当 w k w_k wk距离 w ∗ w^* w∗较近时,SGD会表现出较大的随机性,即 w k w_k wk在 w ∗ w^* w∗附近波动
BGD / MBGD / SGD
| 算法 | 形式 | 说明 |
|---|---|---|
| BGD | w k + 1 = w k − α k 1 n ∑ i = 1 n ∇ w f ( w k , x i ) w_{k+1} = w_k - \alpha_k \frac{1}{n} \sum_{i=1}^{n} \nabla_w f(w_k, x_i) wk+1=wk−αkn1∑i=1n∇wf(wk,xi) | 基于所有采样,最接近于均值 |
| MBGD (mini batch) | w k + 1 = w k − α k 1 m ∑ j ∈ I k ∇ w f ( w k , x j ) w_{k+1} = w_k - \alpha_k \frac{1}{m} \sum_{j \in \mathcal{I}_k} \nabla_w f(w_k, x_j) wk+1=wk−αkm1∑j∈Ik∇wf(wk,xj) | 基于部分采样( ∣ I k ∣ = m ≤ n \vert \mathcal{I}_k \vert=m \leq n ∣Ik∣=m≤n) |
| SGD | w k + 1 = w k − α k ∇ w f ( w k , x k ) w_{k+1} = w_k - \alpha_k \nabla_w f(w_k, x_k) wk+1=wk−αk∇wf(wk,xk) | 基于单个采样 |
MBGD可以视作BGD和SGD的一种中间情况
- m = 1 m=1 m=1:MBGD即为SGD
-
m
=
n
m=n
m=n:MBGD接近于BGD,但不完全相同
- BGD对每个采样使用1次,MBGD是从 n n n个采样中随机选取 n n n次,每个采样被使用的次数可能超过一次【大概是有放回和不放回的区别】