删除链表内指定范围的数

思路是双指针，定义两个指针，一个去找当前这个数满不满足要求，然后另一个定义为删除区间的起点 ，

当不满足时，两个指针同时向后移动；当满足时，前驱指针就不动了，不断的删掉当前的cur,直到为Nullptr或出了区间

node* del(int s, int e, node* head) {
    if (!head)return nullptr;
    node* pre = head, * cur = head->next;//pre表示区间起点，cur表示操作结点
    while (cur) {//只要不空就是还能操作
        if (cur->val <= s) {//当前的结点还不满足操作要求
            pre = cur;
            cur = cur->next;
        }//同时向后移动两个指针
        else {//满足一个要求
            if (cur->val < e) {//满足两个要求
                pre->next = cur->next;//删除掉当前的结点
                cur = cur->next;
            }
            else {
                break;
            }
        }
    }
}

反转链表

双指针

用一个指针，保存为当前遍历到的节点，再来一个指针为当前这个遍历到节点的前一个结点，

这个过程就相当于把链表拆成了两部分，一部分是已经反转好的链表，Pre为其头结点

另一部分为还未反转的原始链表，cur为其头结点，

算法的过程就是不断把未反转的链表的头结点转给反转的链表，让pre去接受

while(cur){//循环条件为，未反转的链表里还有元素，所以就是cur不为空，cur一旦为空就说明为反转的链表已经为空，就不用再反转了

node* temp=cur->next;//保存未反转链表的头结点

cur->next=pre;//把此时未反转链表的头结点接到反转链表上

pre=cur;//更新反转链表的头结点

cur=temp;//更新未反转链表的头结点

}

return pre;//最后返回反转链表的头结点pre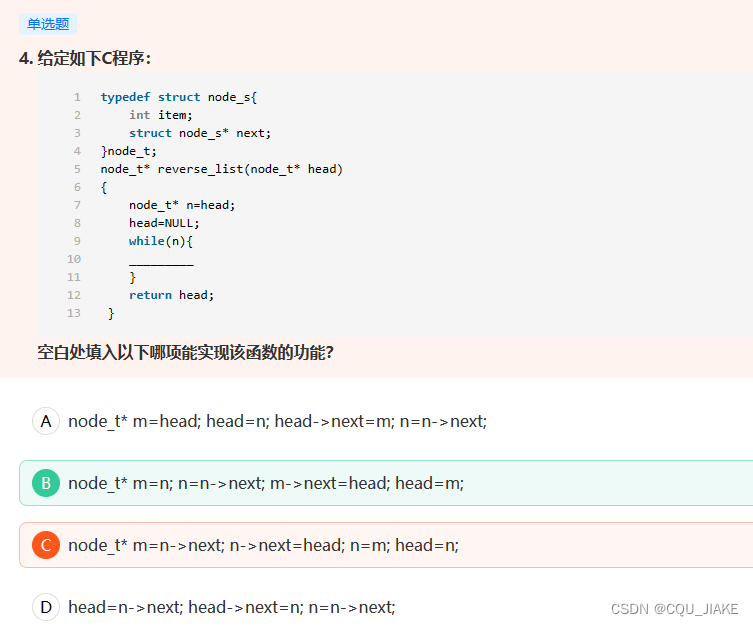

这个C不对，因为更新未排序链表以及已排序链表的顺序反了，应该先更新已倒序的，再更新未倒序的，否则就会导致下一个头结点直接被跳过 

用栈解决

由于栈可以先进先出，所以可以用栈去解决

import java.util.Stack;
public class Solution {
public ListNode ReverseList(ListNode head) {
    Stack<ListNode> stack= new Stack<>();
    //把链表节点全部摘掉放到栈中
    while (head != null) {
        stack.push(head);
        head = head.next;
    }
    if (stack.isEmpty())
        return null;
    ListNode node = stack.pop();
    ListNode dummy = node;
    //栈中的结点全部出栈，然后重新连成一个新的链表
    while (!stack.isEmpty()) {
        ListNode tempNode = stack.pop();
        node.next = tempNode;
        node = node.next;
    }
    //最后一个结点就是反转前的头结点，一定要让他的next
    //等于空，否则会构成环
    node.next = null;
    return dummy;
}
}

链表选择题

top指向栈的顶部，是空结点，然后让新插入的结点下一个指针指向它，

链栈的话，插入是要插入在头结点位置的，即TOP其实是相当于一个头结点的位置，往链栈里插元素，就是在往链表的第一个位置上放元素，所以是C的操作

就是说每个结点都会有两个链域，但是每个结点都会被一个链域唯一确定，除了根节点，所以一共2n个链域，有n-1是被用的，剩下n+1是没被用的

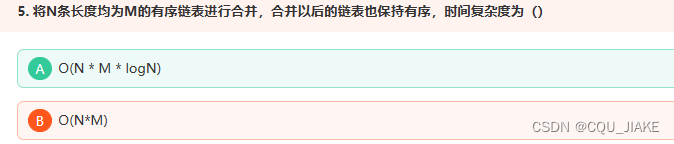
换个思路就是操场跑圈，相对速度为2，跑完一圈的步数为100/2=50 

A.单链表的没个节点都具有唯一的前驱节点和唯一的后继节点，所以当两个单链表存在相交的节点时，这两个链表则同时拥有这个节点，以及这个节点的所有后继节点，当这个公共节点是尾节点时，他们则只含有公共一个节点-------尾节点。 B.快慢指针是判断单链表是否有环的一种方法：两个指针，每次移动的步长为2叫做快指针，每次移动步长为1的指针叫做慢指针。快慢指针同时从头结点出发，当快指针率先到达NULL的时候，则说明此单链表中不存在环，当快指针追上慢指针的时候，说明此单链表中存在环。 C.有环的单向链表和无环的单向链表不能相交，因为当相交的时候，无环的单向链表也会被迫存在一个环，只不过这个环的”起点“可能不是原来单向链表的头结点。 4.两个单向链表之间相交可以存在环。 

两个。 一个每次走一步， 一次每次走两步， 会相遇就表示有环 

尾节点的后继指向头结点，而头结点不是尾节点的逻辑后继

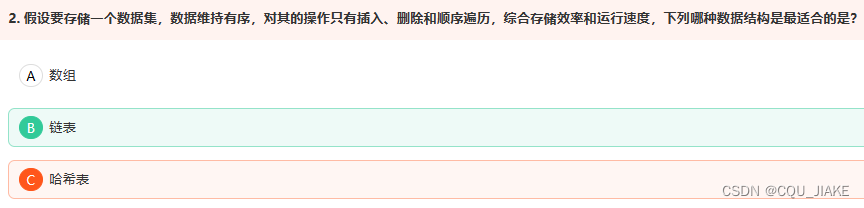
注意是单链表而不是数组 

数组静态分配内存，链表动态分配内存； 数组在内存中连续，链表不连续； 数组元素在栈区，链表元素在堆区； 数组利用下标定位，时间复杂度为O(1)，链表定位元素时间复杂度O(n)； 

数组对象是放在堆内存中，引用是放在栈内存中

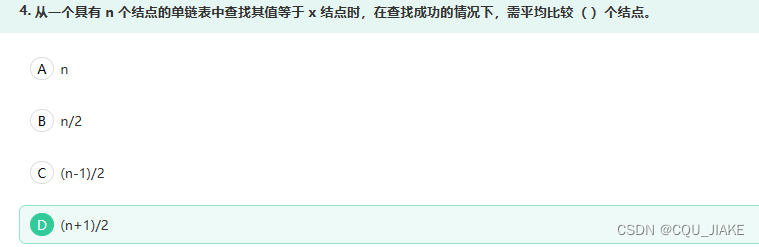
考虑两个极端，最少是1，即头部，最坏是尾部，要N,中间是线性平均，所以为D 

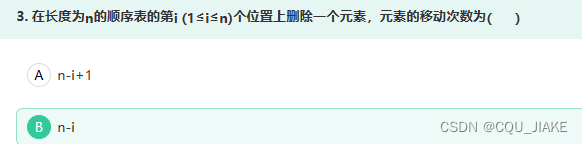
在位置I上删除是N-I,即区间I到N，只含一个端点

在位置I上添加是N-I+1，区间两端点都要 

C除头结点外D考虑空表或只有一个元素

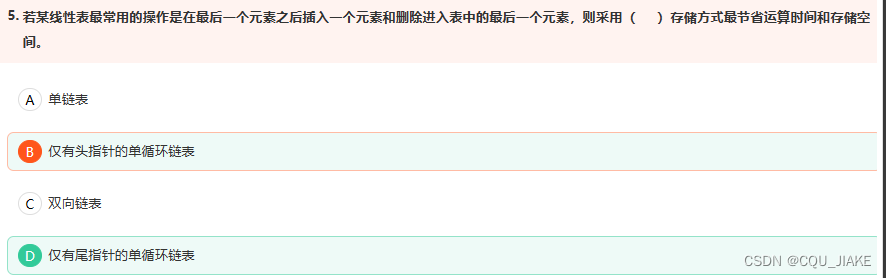
删除元素，删除元素的话需要知道前一个元素的指针；要在指定位置插入，就需要知道指定位置的指针，要删除的话，就是让删除位置的元素前一个元素的指针不再指向它，而是指向空指针或它后面的元素，越过他就行；插入的话就直接在指定位置接上要插入的元素即可

单链表与单循环链表b

b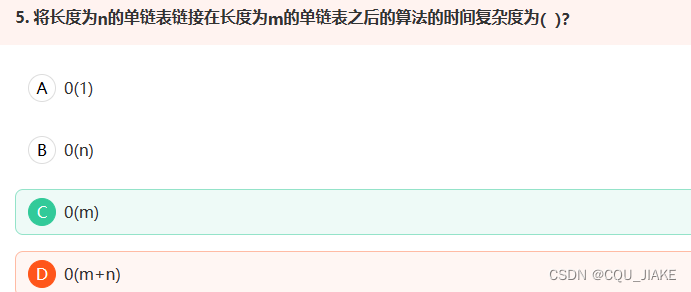

只需要找到被接的链表的尾部，一个OM，然后接的链表，只要头结点即可 

队列

往队列的队尾插入一个元素为入队，从队列的排头删除一个元素称为退队。初始时 front=rear=0 ， front 总是指向队头元素的前一位置，入队一次 rear+1 ，退队一次 front+1 。队列队头队尾指针相同时队列为空。而带链的队列，由于每个元素都包含一个指针域指向下一个元素，当带链队列为空时 front=rear=Null ，插入第 1 个元素时， rear+1 指向该元素， front+1 也指向该元素，插入第 2 个元素时 rear+1 ， front 不变，删除 1 个元素时 front+1 。即 front=rear 不为空时带链的队列中只有一个元素。故本题答案为 A 选项。 

奇怪的选择题

报错

这个需要注意，vector删除后，后续下标会自动往前走，而i++,所以就会导致4被空掉 

广义表

head返回第一个元素，原子，tail返回去掉第一个元素后的表，相当于括号往里缩一个单位 

是广义表以及递归广义表的原理。 广义表是由n个元素组成的序列，n是广义表的长度。 广义表的深度： 广义表中括号的最大层数叫广义表的深度。 F=(a,F)的长度为2，由于属于递归表，所以深度为无穷，F相当于一个无限的表(a,(a,(a,(...))))。 

F的长度为2，第一个元素是原子，第二个元素是F自身。

F的深度为∞。F=(a，F)=(a，(a，(a，(…))))

对任意一个非空的广义表，其表头可能是单元素，也可能是广义表，而其表尾一定是广义表。注意表尾的深度（即括号的嵌套层数），表尾是由除了表头以外的其余元素组成的广义表，所以，需要在表尾的直接元素外面再加一层括号。
广义表最基本的操作：取表头head(LS)与取表尾tail(LS)

例：LS=(a,(b,c,d))
head(LS)=a
tail(LS)=((b,c,d))
head(tail(LS))=(b,c,d)
tail(tail(LS))=()
head(head(tail(LS)))=b
tail(head(tail(LS)))=(c,d)
head(tail(head(tail(LS))))=c
tail(tail(head(tail(LS))))=(d)
head(tail(tail(head(tail(LS)))))=d
tail(tail(tail(head(tail(LS)))))=()