输入一个长度为 n
的整数数列，从小到大输出前 m
小的数。

输入格式
第一行包含整数 n
和 m
。

第二行包含 n
个整数，表示整数数列。

输出格式
共一行，包含 m
个整数，表示整数数列中前 m
小的数。

数据范围
1≤m≤n≤105
，
1≤数列中元素≤109
输入样例：
5 3
4 5 1 3 2
输出样例：
1 2 3

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;
int n, m;
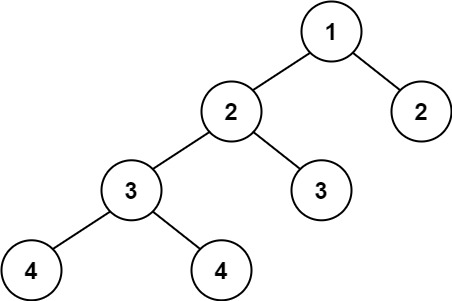
int h[N], size_; //h[1]表示 根结点，2*x表示左子结点，2*x+1表示右子结点

void down(int u)
{
    int t = u;
    if(u * 2 <= size_ && h[u * 2] < h[t]) t = u * 2;//如果左子树存在，并且左子树值比根小
    if(u * 2 + 1 <= size_ && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if(u != t) //如果左右子树中有数小（不等），就交换一下值，并递归down下去。
    {
        swap(h[u], h[t]);
        down(t);
    }
}

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i ++ ) scanf("%d", &h[i]);
    size_ = n;
    
    for(int i = n / 2; i; i -- ) down(i);
    
    while(m --)
    {
        printf("%d ", h[1]); //依次输出最小的，就是根节点
        h[1] = h[size_];
        size_ --;
        down(1);
    }
    return 0;
}

主要就是down的操作。

一般的堆只需要down和up的操作。

void down(int u)
{
    int t = u;
    if(u * 2 <= sizee && h[u * 2] < h[u]) t = u * 2;
    if(u * 2 + 1 <= sizee && h[u * 2 + 1] < h[u]) t = u * 2 + 1;
    if(u != t)
    {
        swap(h[u], h[t]);
        down(t);
    }
}

void up(int u)
{
    while(u / 2 && h[u / 2] > h[u]) //如果父节点存在 且 父节点比自己大，就交换。迭代下去
    {
        swap(h[u / 2], h[u]);
        u /= 2;
    }
}