价值迭代算法

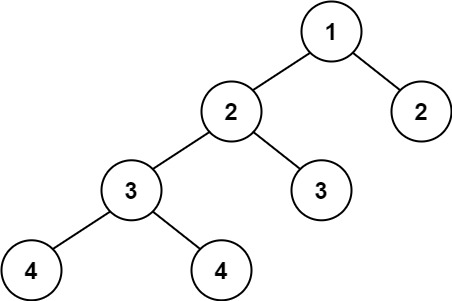
价值迭代算法相对于策略迭代更加直接，它直接根据以下公式来迭代更新。
    V ∗ ( s ) = max ⁡ a ∈ A { r ( s , a ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s , a ) V ∗ ( s ′ ) }    V^*(s)=\max_{a\in\mathcal{A}}\{r(s,a)+\gamma\sum_{s'\in\mathcal{S}}P(s'|s,a)V^*(s')\}    V∗(s)=a∈Amax​{r(s,a)+γs′∈S∑​P(s′∣s,a)V∗(s′)} 
之后使用下面的公式找到最优策略即可。
π ( s ) = arg ⁡ max ⁡ a { r ( s , a ) + γ ∑ s ′ p ( s ′ ∣ s , a ) V k + 1 ( s ′ ) } \pi(s)=\arg\max_{a}\{r(s,a)+\gamma\sum_{s^{\prime}}p(s^{\prime}|s,a)V^{k+1}(s^{\prime})\} π(s)=argamax​{r(s,a)+γs′∑​p(s′∣s,a)Vk+1(s′)}

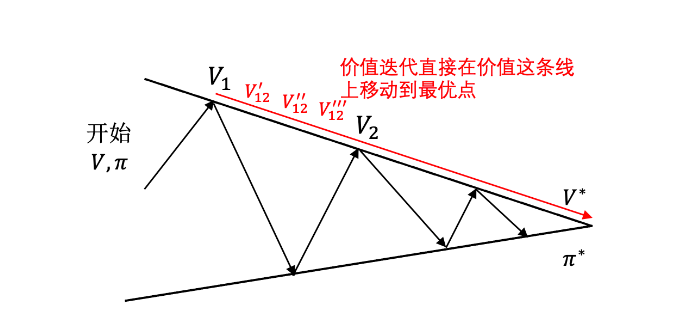
策略迭代是更新完状态价值函数后，更新策略，之后再更新状态价值函数；而价值迭代，先不断迭代状态价值函数，一次性得到贪心最优策略。但是策略迭代过程中，是由V1直接到了V2，会跳过过程中的一些点，但是在价值迭代时候，需要从$V_1\to V_{12}^{\prime }\to V_{12}^{\prime \prime }$ 这些点，比较费时间。

流程如下所示：

• 随机初始化 $V(s)$
• $while\Delta >\theta do：$
  • $\Delta \leftarrow 0$
  • 对于每一个状态$s\in S$:
    • $v\leftarrow V(s)$
    • $V(s)\leftarrow {\max }_{a}r(s,a)+\gamma {\sum }_{s^{\prime }}P(s^{\prime }|s,a)V(s^{\prime })$
    • $\Delta \leftarrow max(\Delta ,|v-V(s)|)$
• end while
• 返回一个确定的策略 π ( s ) = arg ⁡ max ⁡ a { r ( s , a ) + γ ∑ s ′ P ( s ′ ∣ s , a ) V ( s ′ ) } \pi(s)=\arg\max_a\{r(s,a)+\gamma\sum_{s^{\prime}}P(s^{\prime}|s,a)V(s^{\prime})\} π(s)=argmaxa​{r(s,a)+γ∑s′​P(s′∣s,a)V(s′)}

价值迭代的代码如下所示：

class ValueIteration():
    def __init__(self,env,theta,gamma):
        self.env=env
        self.v=[0]*env.ncol*env.nrow # 初始化价值为0
        self.theta=theta
        self.gamma=gamma
        # 价值迭代结束后得到的策略
        self.pi=[None for i in range(self.env.ncol*self.env.nrow)]
        
    def valueIteration(self):
        cnt =0
        while 1:
            maxDiff=0
            newV=[0]*self.env.ncol*self.env.nrow
            for s in range(self.env.ncol*self.env.nrow):
                qsaList=[]
                for a in range(4):
                    qsa=0
                    for transition in self.env.P[s][a]:
                        p,nextState,r,done=transition
                        qsa+=p*(r+self.gamma*self.v[nextState]*(1-done))
                    qsaList.append(qsa)
                newV[s]=max(qsaList)
                maxDiff=max(maxDiff,abs(newV[s]-self.v[s]))
            self.v=newV
            if maxDiff<self.theta: break
            cnt+=1
        print("价值迭代一共进行%d轮" % cnt)
        self.getPolicy()
        
    def getPolicy(self):
        # 根据价值函数导出一个贪婪策略
        for s in range(self.env.ncol*self.env.nrow):
            qsaList=[]
            for a in range(4):
                qsa=0
                for transition in self.env.P[s][a]:
                    p,nextState,r,done=transition
                    qsa+=p*(r+self.gamma*self.v[nextState]*(1-done))
                qsaList.append(qsa)
            maxq=max(qsaList)
            cntq=qsaList.count(maxq)
            self.pi[s]=[1/cntq if q==maxq else 0 for q in qsaList]
            
env = CliffWalkingEnv()
action_meaning = ['^', 'v', '<', '>']
theta = 0.001
gamma = 0.9
agent = ValueIteration(env, theta, gamma)
agent.valueIteration()

价值迭代一共进行14轮
状态价值：
-7.712 -7.458 -7.176 -6.862 -6.513 -6.126 -5.695 -5.217 -4.686 -4.095 -3.439 -2.710
-7.458 -7.176 -6.862 -6.513 -6.126 -5.695 -5.217 -4.686 -4.095 -3.439 -2.710 -1.900
-7.176 -6.862 -6.513 -6.126 -5.695 -5.217 -4.686 -4.095 -3.439 -2.710 -1.900 -1.000
-7.458  0.000  0.000  0.000  0.000  0.000  0.000  0.000  0.000  0.000  0.000  0.000
策略：
ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovoo
ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovoo
ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ovoo
^ooo **** **** **** **** **** **** **** **** **** **** EEEE