文章目录
- 1 二叉树概念
- 2 二叉树的存储和编码
- 2.1 二叉树的存储方法
- 2.2 二叉树存储的编码实现
- 2.3 二叉树的极简存储方法
- 3 例题
- 4 习题
前面介绍的数据结构数组、队列、栈,都是线性的,它们存储数据的方式是把相同类型的数据按顺序一个接一个串在一起。简单的形态使线性表难以实现高效率的操作。
二叉树是一种层次化的、高度组织性的数据结构。二叉树的形态使得它有天然的优势,在二叉树上做查询、插入、删除、修改、区间等操作极为高效,基于二叉树的算法也很容易实现高效率的计算。
1 二叉树概念
二叉树的每个节点最多有两个子节点,分别称为左孩子、右孩子,以它们为根的子树称为左子树、右子树。二叉树的每一层以2的倍数递增,所以二叉树的第k层最多有 2 k − 1 2^{k-1} 2k−1 个节点。根据每一层的节点分布情况,有以下常见的二叉树。
(1)满二叉树
特征是每一层的节点数都是满的。第一层只有1个节点,编号为1;第二层有2个节点,编号2、3;第三层有4个节点,编号4、5、6、7;…;第k层有 2 k − 1 2^{k-1} 2k−1 个节点,编号 2 k − 1 2^{k-1} 2k−1、 2 k − 1 + 1 2^{k-1}+1 2k−1+1、…、 2 k − 1 2^k-1 2k−1。
一棵n层的满二叉树,节点一共有 1 + 2 + 4 + . . . + 2 n − 1 = 2 n − 1 1+2+4+...+2^{n-1} = 2^{n-1} 1+2+4+...+2n−1=2n−1 个。
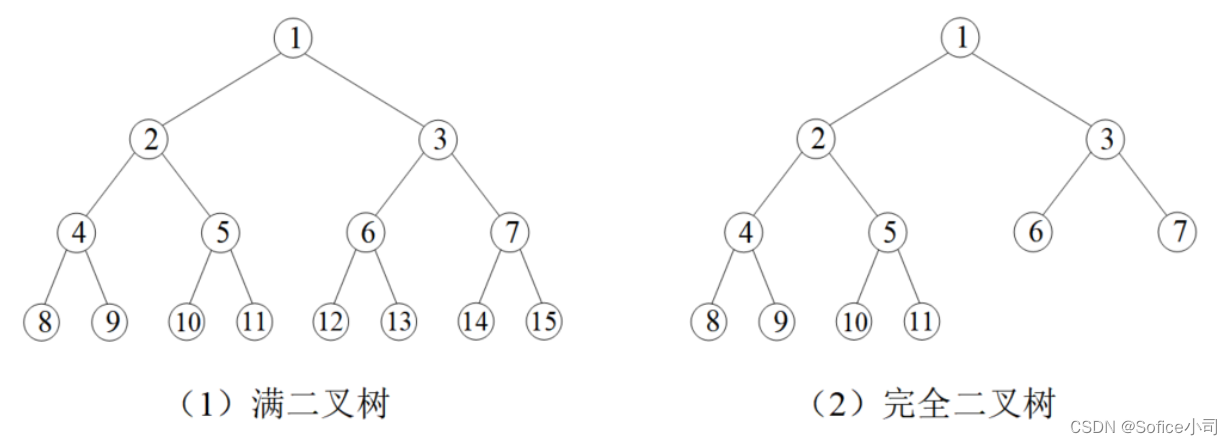
(2)完全二叉树
如果满二叉树只在最后一层有缺失,并且缺失的节点都在最后,称为完全二叉树。上图演示了一棵满二叉树和一棵完全二叉树。
(3)平衡二叉树
任意左子树和右子树的高度差不大于1,称为平衡二叉树。若只有少部分子树的高度差超过1,这是一棵接近平衡的二叉树。
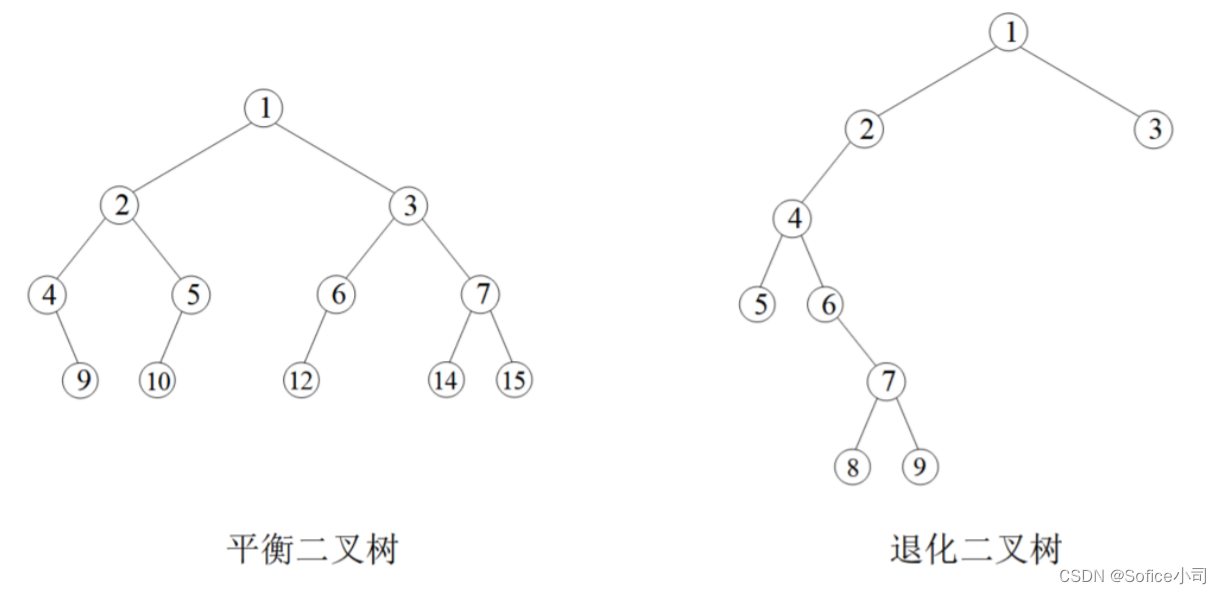
(4)退化二叉树
如果树上每个节点都只有1个孩子,称为退化二叉树。退化二叉树实际上已经变成了一根链表。如果绝大部分节点只有1个孩子,少数有2个孩子,也看成退化二叉树。
二叉树之所以应用广泛,得益于它的形态。高级数据结构大部分和二叉树有关,下面列举二叉树的一些优势。
(1)在二叉树上能进行极高效率的访问。一棵平衡的二叉树,例如满二叉树或完全二叉树,每一层的节点数量约是上一层数量的2倍,也就是说,一棵有N个节点的满二叉树,树的高度是O(logN)。从根节点到叶子节点,只需要走logN步,例如N = 100万,树的高度仅有logN = 20,只需要20步就能到达100万个节点中的任意一个。但是,如果二叉树不是满的,而且很不平衡,甚至在极端情况下变成退化二叉树,访问效率会打折扣。维护二叉树的平衡是高级数据结构的主要任务之一。
(2)二叉树很适合做从整体到局部、从局部到整体的操作。二叉树内的一棵子树可以看成整棵树的一个子区间,求区间最值、区间和、区间翻转、区间合并、区间分裂等,用二叉树都很快捷。
(3)基于二叉树的算法容易设计和实现。例如二叉树用BFS和DFS搜索处理都极为简便。二叉树可以一层一层地搜索,这是BFS。二叉树的任意一个子节点,是以它为根的一棵二叉树,这是一种递归的结构,用DFS访问二叉树极容易编码。
2 二叉树的存储和编码
2.1 二叉树的存储方法
要使用二叉树,首先得定义和存储它的节点。
二叉树的一个节点包括三个值:节点的值、指向左孩子的指针、指向右孩子的指针。需要用一个结构体来定义二叉树。
二叉树的节点有动态和静态两种存储方法,竞赛中一般采用静态方法。
(1)动态存储二叉树。例如写c代码,数据结构的教科书一般这样定义二叉树的节点:
struct Node{
int value; //节点的值,可以定义多个值
Node *lson, *rson; //指针,分别指向左右子节点
};
其中value是这个节点的值,lson和rson是指向两个孩子的指针。动态新建一个Node时,用new运算符动态申请一个节点。使用完毕后,需要用delete释放它,否则会内存泄漏。动态二叉树的优点是不浪费空间,缺点是需要管理,不小心会出错,竞赛中一般不这样用。
(2)用静态数组存储二叉树。在算法竞赛中,为了编码简单,加快速度,一般用静态数组来实现二叉树。下面定义一个大小为N的结构体数组。N的值根据题目要求设定,有时节点多,例如N=100万,那么tree[N]使用的内存是12M字节,不算大。
struct Node{ //静态二叉树
int value; //可以把value简写为v
int lson, rson; //左右孩子,可以把lson、rson简写为ls、rs
}tree[N]; //可以把tree简写为t
tree[i]表示这个节点存储在结构体数组的第i个位置,lson是它的左孩子在结构体数组的位置,rson是它的右孩子在结构体数组的位置。lson和rson指向孩子的位置,也可以称为指针。
下图演示了一棵二叉树的存储,圆圈内的字母是这个节点的value值。根节点存储在tree[5]上,它的左孩子lson=7,表示左孩子存储在tree[7]上,右孩子rson=3,存储在tree[3]。
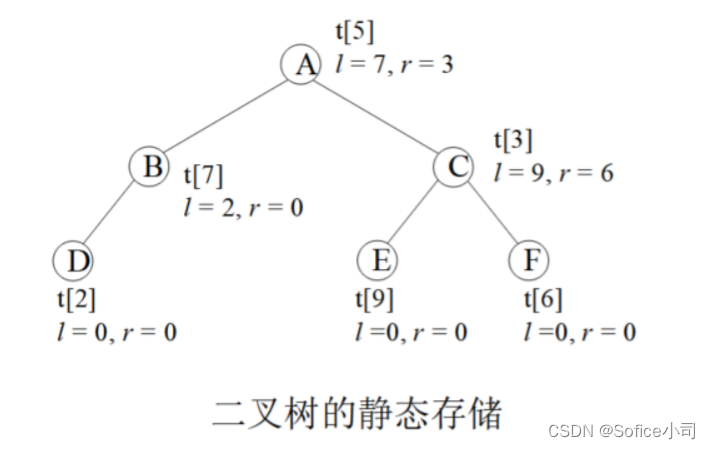
编码时一般不用tree[0],因为0常常被用来表示空节点,例如叶子节点tree[2]没有子节点,就把它的子节点赋值为lson = rson = 0。
2.2 二叉树存储的编码实现
下面写代码演示上图中二叉树的建立,并输出二叉树。
(1)C++代码。第16~21行建立二叉树,然后用print_tree()输出二叉树。
#include <bits/stdc++.h>
using namespace std;
const int N=100; //注意const不能少
struct Node{ //定义静态二叉树结构体
char v; //把value简写为v
int ls, rs; //左右孩子,把lson、rson简写为ls、rs
}t[N]; //把tree简写为t
void print_tree(int u){ //打印二叉树
if(u){
cout<<t[u].v<<' '; //打印节点u的值
print_tree(t[u].ls); //继续搜左孩子
print_tree(t[u].rs); //继续搜右孩子
}
}
int main(){
t[5].v='A'; t[5].ls=7; t[5].rs=3;
t[7].v='B'; t[7].ls=2; t[7].rs=0;
t[3].v='C'; t[3].ls=9; t[3].rs=6;
t[2].v='D'; // t[2].ls=0; t[2].rs=0; 可以不写,因为t[]是全局变量,已初始化为0
t[9].v='E'; // t[9].ls=0; t[9].rs=0; 可以不写
t[6].v='F'; // t[6].ls=0; t[6].rs=0; 可以不写
int root = 5; //根是tree[5]
print_tree(5); //输出: A B D C E F
return 0;
}
初学者可能看不懂print_tree()是怎么工作的。它是一个递归函数,先打印这个节点的值t[u].v,然后继续搜它的左右孩子。上图的打印结果是”A B D C E F”,步骤如下:
(1)首先打印根节点A;
(2)然后搜左孩子,是B,打印出来;
(3)继续搜B的左孩子,是D,打印出来;
(4)D没有孩子,回到B,B发现也没有右孩子,继续回到A;
(5)A有右孩子C,打印出来;
(6)打印C的左右孩子E、F。
这个递归函数执行的步骤称为“先序遍历”,先输出父节点,然后再搜左右孩子并输出。还有“中序遍历”和“后序遍历”,将在后面讲解。
(2)Java代码
import java.util.*;
class Main {
static class Node {
char v;
int ls, rs;
}
static final int N = 100;
static Node[] t = new Node[N];
static void print_tree(int u) {
if (u != 0) {
System.out.print(t[u].v + " ");
print_tree(t[u].ls);
print_tree(t[u].rs);
}
}
public static void main(String[] args) {
t[5] = new Node(); t[5].v = 'A'; t[5].ls = 7; t[5].rs = 3;
t[7] = new Node(); t[7].v = 'B'; t[7].ls = 2; t[7].rs = 0;
t[3] = new Node(); t[3].v = 'C'; t[3].ls = 9; t[3].rs = 6;
t[2] = new Node(); t[2].v = 'D';
t[9] = new Node(); t[9].v = 'E';
t[6] = new Node(); t[6].v = 'F';
int root = 5;
print_tree(5); // 输出: A B D C E F
}
}
(3)Python代码
N = 100
class Node: # 定义静态二叉树结构体
def __init__(self):
self.v = '' # 把value简写为v
self.ls = 0 # 左右孩子,把lson、rson简写为ls、rs
self.rs = 0
t = [Node() for i in range(N)] # 把tree简写为t
def print_tree(u):
if u:
print(t[u].v, end=' ') # 打印节点u的值
print_tree(t[u].ls)
print_tree(t[u].rs)
t[5].v, t[5].ls, t[5].rs = 'A', 7, 3
t[7].v, t[7].ls, t[7].rs = 'B', 2, 0
t[3].v, t[3].ls, t[3].rs = 'C', 9, 6
t[2].v = 'D' # t[2].ls=0; t[2].rs=0; 可以不写,因为t[]已初始化为0
t[9].v = 'E' # t[9].ls=0; t[9].rs=0; 可以不写
t[6].v = 'F' # t[6].ls=0; t[6].rs=0; 可以不写
root = 5 # 根是tree[5]
print_tree(5) # 输出: A B D C E F
2.3 二叉树的极简存储方法
如果是满二叉树或者完全二叉树,有更简单的编码方法,连lson、rson都不需要定义,因为可以用数组的下标定位左右孩子。
一棵节点总数量为k的完全二叉树,设1号点为根节点,有以下性质:
(1)
p
>
1
p > 1
p>1的节点,其父节点是
⌊
p
/
2
⌋
\lfloor p/2 \rfloor
⌊p/2⌋。例如
p
=
4
p=4
p=4,父亲是
4
/
2
=
2
4/2=2
4/2=2;
p
=
5
p=5
p=5,父亲是
5
/
2
=
2
5/2=2
5/2=2。
(2)如果
2
×
p
>
k
2×p> k
2×p>k,那么
p
p
p没有孩子;如果
2
×
p
+
1
>
k
2×p+1 > k
2×p+1>k,那么
p
p
p没有右孩子。例如
k
=
11
k=11
k=11,
p
=
6
p=6
p=6的节点没有孩子;
k
=
12
k=12
k=12,
p
=
6
p=6
p=6的节点没有右孩子。
(3)如果节点
p
p
p有孩子,那么它的左孩子是
2
×
p
2×p
2×p,右孩子是
2
×
p
+
1
2×p+1
2×p+1。
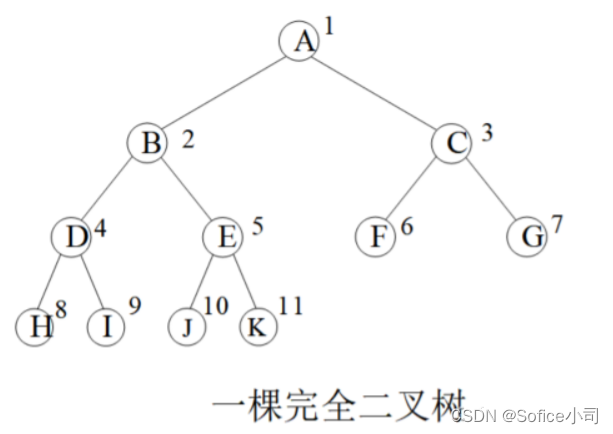
图中圆圈内是节点的值,圆圈外数字是节点存储位置。
(1)C++代码。
用 l s ( p ) ls(p) ls(p)找p的左孩子,用 r s ( p ) rs(p) rs(p)找p的右孩子。 l s ( p ) ls(p) ls(p)中把 p ∗ 2 p*2 p∗2写成 p < < 1 p<<1 p<<1,用了位运算。
#include <bits/stdc++.h>
using namespace std;
const int N=100; //注意const不能少
char t[N]; //简单地用一个数组定义二叉树
int ls(int p){return p<<1;} //定位左孩子,也可以写成 p*2
int rs(int p){return p<<1 | 1;} //定位右孩子,也可以写成 p*2+1
int main(){
t[1]='A'; t[2]='B'; t[3]='C';
t[4]='D'; t[5]='E'; t[6]='F'; t[7]='G';
t[8]='H'; t[9]='I'; t[10]='J'; t[11]='K';
cout<<t[1]<<":lson="<<t[ls(1)]<<" rson="<<t[rs(1)]; //输出 A:lson=B rson=C
cout<<endl;
cout<<t[5]<<":lson="<<t[ls(5)]<<" rson="<<t[rs(5)]; //输出 E:lson=J rson=K
return 0;
}
(2)Java代码。
import java.util.Arrays;
public class Main {
static int ls(int p){ return p<<1;}
static int rs(int p){ return p<<1 | 1;}
public static void main(String[] args) {
final int N = 100;
char[] t = new char[N];
t[1]='A'; t[2]='B'; t[3]='C';
t[4]='D'; t[5]='E'; t[6]='F'; t[7]='G';
t[8]='H'; t[9]='I'; t[10]='J'; t[11]='K';
System.out.print(t[1]+":lson="+t[ls(1)]+" rson="+t[rs(1)]);//输出A:lson=B rson=C
System.out.println();
System.out.print(t[5]+":lson="+t[ls(5)]+" rson="+t[rs(5)]);//输出E:lson=J rson=K
}
}
(3)Python代码。
N = 100
t = [''] * N
def ls(p): return p << 1
def rs(p): return (p << 1) | 1
t[1] = 'A'; t[2] = 'B'; t[3] = 'C'
t[4] = 'D'; t[5] = 'E'; t[6] = 'F'; t[7] = 'G'
t[8] = 'H'; t[9] = 'I'; t[10] = 'J'; t[11] = 'K'
print(t[1] + ':lson=' + t[ls(1)] + ' rson=' + t[rs(1)]) # 输出 A:lson=B rson=C
print(t[5] + ':lson=' + t[ls(5)] + ' rson=' + t[rs(5)]) # 输出 E:lson=J rson=K
其实,即使二叉树不是完全二叉树,而是普通二叉树,也可以用这种简单方法来存储。如果某个节点没有值,那就空着这个节点不用,方法是把它赋值为一个不该出现的值,例如赋值为0或无穷大INF。这样会浪费一些空间,好处是编程非常简单。
3 例题
二叉树是很基本的数据结构,大量算法、高级数据结构都是基于二叉树的。二叉树有很多操作,最基础的操作是搜索(遍历)二叉树的每个节点,有先序遍历、中序遍历、后序遍历。这3种遍历都用到了递归函数,二叉树的形态天然适合用递归来编程。
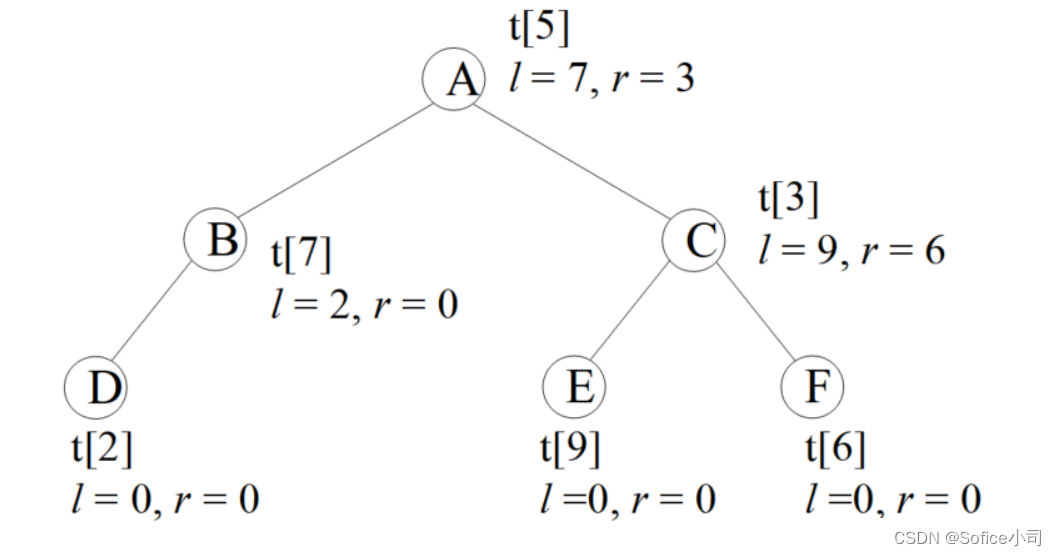
(1)先(父)序遍历,父节点在最前面输出。先输出父节点,再访问左孩子,最后访问右孩子。上图的先序遍历结果是ABDCEF。为什么?把结果分解为:A-BD-CEF。父亲是A,然后是左孩子B和它带领的子树BD,最后是右孩子C和它带领的子树CEF。这是一个递归的过程,每个子树也满足先序遍历,例如CEF,父亲是C,然后是左孩子E,最后是右孩子F。
(2)中(父)序遍历,父节点在中间输出。先访问左孩子,然后输出父节点,最后访问右孩子。上图的中序遍历结果是DBAECF。为什么?把结果分解为:DB-A-ECF。DB是左子树,然后是父亲A,最后是右子树ECF。每个子树也满足中序遍历,例如ECF,先左孩子E,然后是父亲C,最后是右孩子F。
(3)后(父)序遍历,父节点在最后输出。先访问左孩子,然后访问右孩子,最后输出父节点。上图的后序遍历结果是DBEFCA。为什么?把结果分解为:DB-EFC-A。DB是左子树,然后是右子树EFC,最后是父亲A。每个子树也满足后序遍历,例如EFC,先左孩子E,然后是右孩子F,最后是父亲C。
这三种遍历,中序遍历是最有用的,它是二叉查找树的核心。
例题 二叉树的遍历
(1)C++代码
#include <bits/stdc++.h>
using namespace std;
const int N = 100005;
struct Node{
int v; int ls, rs;
}t[N]; //tree[0]不用,0表示空结点
void preorder (int p){ //求先序序列
if(p != 0){
cout << t[p].v <<" "; //先序输出
preorder (t[p].ls);
preorder (t[p].rs);
}
}
void midorder (int p){ //求中序序列
if(p != 0){
midorder (t[p].ls);
cout << t[p].v <<" "; //中序输出
midorder (t[p].rs);
}
}
void postorder (int p){ //求后序序列
if(p != 0){
postorder (t[p].ls);
postorder (t[p].rs);
cout << t[p].v <<" "; //后序输出
}
}
int main() {
int n; cin >> n;
for (int i = 1; i <= n; i++) {
int a, b; cin >> a >> b;
t[i].v = i;
t[i].ls = a;
t[i].rs = b;
}
preorder(1); cout << endl;
midorder(1); cout << endl;
postorder(1); cout << endl;
}
(2)Java代码
下面的Java代码和上面的C++代码略有不同。例如在preorder()中没有直接打印节点的值,而是用joiner.add()先记录下来,遍历结束后一起打印,这样快一些。本题 n = 1 0 6 n=10^6 n=106 ,规模大,时间紧张。
import java.util.Scanner;
import java.util.StringJoiner;
class Main {
static class Node {
int v, ls, rs;
Node(int v, int ls, int rs) {
this.v = v;
this.ls = ls;
this.rs = rs;
}
}
static final int N = 100005;
static Node[] t = new Node[N]; //tree[0]不用,0表示空结点
static void preorder(int p, StringJoiner joiner) { //求先序序列
if (p != 0) {
joiner.add(t[p].v + ""); //不是直接打印,而是先记录下来
preorder(t[p].ls,joiner);
preorder(t[p].rs,joiner);
}
}
static void midorder(int p, StringJoiner joiner) { //求中序序列
if (p != 0) {
midorder(t[p].ls,joiner);
joiner.add(t[p].v + "");//中序输出
midorder(t[p].rs,joiner);
}
}
static void postorder(int p, StringJoiner joiner) { //求后序序列
if (p != 0) {
postorder(t[p].ls,joiner);
postorder(t[p].rs,joiner);
joiner.add(t[p].v + ""); //后序输出
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
for (int i = 1; i <= n; i++) {
int a = sc.nextInt(), b = sc.nextInt();
t[i] = new Node(i, a, b);
}
StringJoiner joiner = new StringJoiner(" ");
preorder(1, joiner); System.out.println(joiner);
joiner = new StringJoiner(" ");
midorder(1, joiner); System.out.println(joiner);
joiner = new StringJoiner(" ");
postorder(1, joiner); System.out.println(joiner);
}
}
(3)Python代码
N = 100005
t = [0] * N # tree[0]不用,0表示空结点
class Node:
def __init__(self, v, ls, rs):
self.v = v
self.ls = ls
self.rs = rs
def preorder(p): # 求先序序列
if p != 0:
print(t[p].v, end=' ') # 先序输出
preorder(t[p].ls)
preorder(t[p].rs)
def midorder(p): # 求中序序列
if p != 0:
midorder(t[p].ls)
print(t[p].v, end=' ') # 中序输出
midorder(t[p].rs)
def postorder(p): # 求后序序列
if p != 0:
postorder(t[p].ls)
postorder(t[p].rs)
print(t[p].v, end=' ') # 后序输出
n = int(input())
for i in range(1, n+1):
a, b = map(int, input().split())
t[i] = Node(i, a, b)
preorder(1); print()
midorder(1); print()
postorder(1); print()
4 习题
完全二叉树的权值
FBI树
American Heritage
求先序排列




![[AutoSar]基础部分 RTE 04 数据类型的定义及使用](https://img-blog.csdnimg.cn/direct/0d1ffc6be4ec4ec9a6d077cb2a99855f.png)