本篇博客将详细讲解二叉搜索树。
文章目录
- 二叉搜索树
- 概念
- 操作
- 查找
- 插入
- 删除
- 性能分析
- 结尾
二叉搜索树
概念
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树
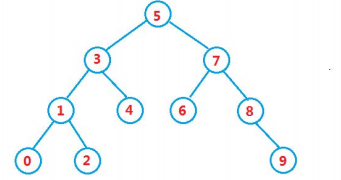
操作
查找
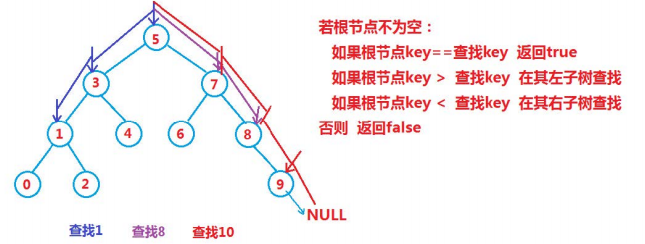
示例代码
class Node {
public int val;
public Node left;
public Node right;
public Node(int val) {
this.val = val;
}
}
public class BinarySearchTree {
public Node root = null;
public Node search(int key) {
Node cur = root;
while (cur != null) {
if (cur.val < key) {
cur = cur.right;
} else if (cur.val == key) {
return cur;
} else {
cur = cur.left;
}
}
return null;
}
}
插入
具体步骤:
-
如果树为空树,即根 == null,直接插入
-
如果树不是空树,按照查找逻辑确定插入位置,插入新结点
示例代码
public boolean insert(int val) {
if (root == null) {
root = new Node(val);
return true;
}
Node cur = root;
Node parent = null;
while (cur != null) {
if (cur.val < val) {
parent = cur;
cur = cur.right;
} else if (cur.val == val) {
return false;//不能有相同的数据
} else {
parent = cur;
cur = cur.left;
}
}
Node node = new Node(val);
if (parent.val < val) {
parent.right = node;
} else {
parent.left = node;
}
return true;
}
删除
设待删除结点为 cur, 待删除结点的双亲结点为parent
- cur.left == null
-
cur 是 root,则 root = cur.right
-
cur 不是 root,cur 是 parent.left,则 parent.left = cur.right
-
cur 不是 root,cur 是 parent.right,则 parent.right = cur.right
- cur.right == null
-
cur 是 root,则 root = cur.left
-
cur 不是 root,cur 是 parent.left,则 parent.left = cur.left
-
cur 不是 root,cur 是 parent.right,则 parent.right = cur.left
- cur.left != null && cur.right != null
- 需要使用替换法进行删除,即在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删除节点中,再来处理该结点的删除问题
示例代码
public void remove(int key) {
Node cur = root;
Node parent = null;
while (cur != null) {
if (cur.val == key) {
removeNode(cur,parent);
break;
}else if (cur.val < key) {
parent = cur;
cur = cur.right;
} else {
parent = cur;
cur = cur.left;
}
}
}
public void removeNode(Node cur, Node parent) {
if (cur.left == null) {
if (cur == root) {
root = cur.right;
} else if (cur == parent.left) {
parent.left = cur.right;
} else {
parent.right = cur.right;
}
} else if (cur.right == null) {
if (cur == root) {
root = cur.left;
} else if (cur == parent.left) {
parent.left = cur.left;
} else {
parent.right = cur.left;
}
} else {
Node targetParent = cur;
Node target = cur.right;
while (target.left != null) {
targetParent = target;
target = target.left;
}
cur.val = target.val;
if (target == targetParent.left) {
targetParent.left = target.right;
} else {
targetParent.right = target.right;
}
}
}
性能分析
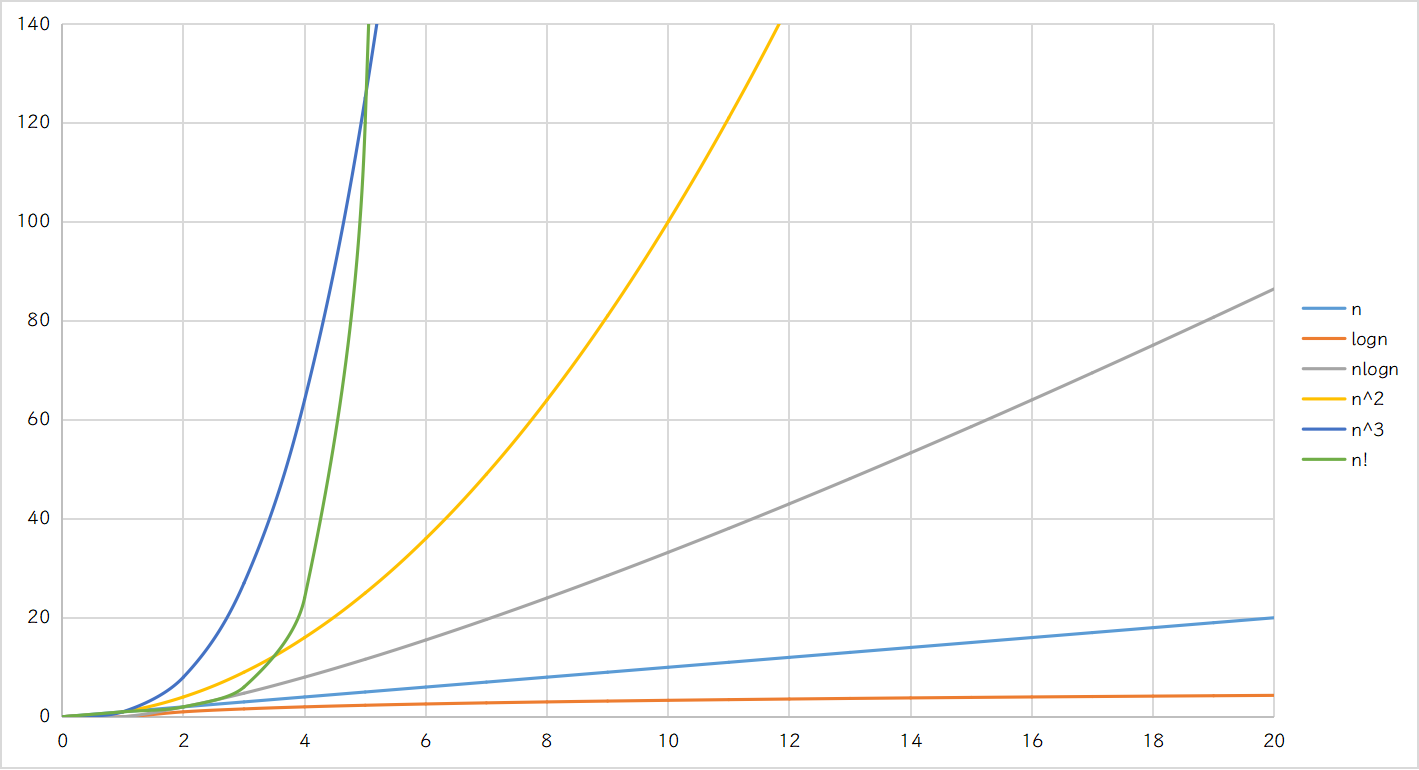
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数,即结点越深,则比较次数越多。但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
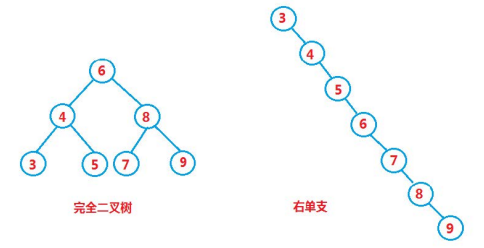
最优情况下,二叉搜索树为完全二叉树,其平均比较次数为:log(N)
最差情况下,二叉搜索树退化为单支树,其平均比较次数为:N/2
结尾
本篇博客到此结束。
上一篇博客:Java学习苦旅(二十二)——Map&Set
下一篇博客:Java学习苦旅(二十四)——Java中的内部类




![[大厂实践] 重新发明后端子集](https://img-blog.csdnimg.cn/img_convert/1489983b6b3f46fae77318d37aa6279d.png)