[王有志](https://www.yuque.com/wangyouzhi-u3woi/dfhnl0/hqrch62un0cc9sp2?singleDoc# 《🔥快来关注我》),一个分享硬核Java技术的互金摸鱼侠
加入Java人的提桶跑路群:[共同富裕的Java人](https://www.yuque.com/wangyouzhi-u3woi/dfhnl0/nwry2mdlktok50bt?singleDoc# 《🔥共同富裕的Java人》)
今天我们只有一个内容:算法的复杂度分析。算法的复杂度分析可以说是算法中的灵魂,有了它我们才能去评价一个算法优劣。
算法的评价标准
我们可以套用“多快好省”这个标准去衡量算法:
- 多,适用场景多,适用于一个问题的算法没有太大的意义;
- 快,运行速度快,过慢的算法没有太大的意义;
- 好,代码质量好,优雅的实现和健壮的程序;
- 省,占用资源省,用得越省算法越好。
有了衡量算法的标准,我们还需要一套衡量算法的方法。
算法的复杂度分析
算法是解决一类问题思想,因此我们不必关注多的标准;好的标准虽然有一定的共识,如可读性,健壮性,但是无法量化。而快和省是通过执行时间和内存占用来体现的,可以进行量化分析。
通常我们将算法的执行时间和内存占用统称为算法执行效率,而对算法执行效率的分析称为算法复杂度分析。
算法的执行效率,会受到问题规模和硬件环境的影响。在设计算法时,我们无法预测算法执行的硬件环境,因此我们需要一种能够忽略硬件环境,并能客观展示算法的执行效率随问题规模增长而改变的分析方法。
渐进复杂度分析
相信你一定听说过“大O记号”和“(渐进)时间复杂度”吧?
实际上这就是通过渐进分析得到的结果。我们先来看下邓俊峰老师的解释:
在评价算法运行效率时,我们往往可以忽略其处理小规模问题时的能力差异,转而关注其在处理更大规模问题时的表现。其中的原因不难理解,小规模问题所需的处理时间本来就相对更少,故此时不同算法的实际效率差异并不明显;而在处理更大规模的问题时,效率的些许差异都将对实际执行效果产生巨大的影响。这种着眼长远、更为注重时间复杂度的总体变化趋势和增长速度的策略与方法,即所谓的渐进分析(asymptotic analysis)。
这段话不难理解,简单来说就是,渐进分析关注的是算法执行效率随问题规模增长的变化趋势和增长速度。如果绘制成函数曲线,我们就是要看这条曲线“陡不陡”。
如果将执行效率拆分开来,算法的复杂度又可以分为渐进时间复杂度和渐进空间复杂度。
渐进时间复杂度分析中,可以粗略的认为每行代码的执行时间是一致的,从而对代码执行次数进行分析。如果借助了编程语言的工具库,还需要考虑这部分的时间成本。
渐进空间复杂度分析中,原始输入的数据不计入到空间占用中,只有在算法中创建的才会计入。
随着硬件技术的发展,内存越来越廉价,在设计算法时,也可以考虑通过使用更多的内存,来换取更快的执行速度,即常说的空间换时间。不过,如果想要设计一个好的算法,还是需要两者兼顾的,在保证极低的时间成本下,尽可能的压缩空间成本。
大O记号
渐进分析中,我们通常使用大O记号来表示分析的结果。不必过多的关注大O记号的由来,只需要记住大O记号为了刻画变化趋势和增长速度,可以忽略掉常数项和低次项。
邓俊峰老师也给出了大O记号的结论:
在大O记号的意义下,函数各项正的常系数可以忽略并等同于1。多项式中的低次项均可忽略,只需保留最高次项。可以看出,大O记号的这些性质的确体现了对函数总体渐进增长趋势的关注和刻画。
我们不难看出,大O记号使用最高次项表示算法的复杂度,是一种对算法复杂度最坏情况的估算。
大Ω记号和大Θ记号
除了大O记号外,用来表示算法复杂度的还有大Ω记号和大Θ记号,不过由于使用较少,我们在这里只引用邓俊峰老师的一句解释:
这里的称作“大Ω记号”(big-Ω notation)。与大O记号恰好相反,大Ω记号是对算法执行效率的乐观估计。
也就是说,大Ω记号是用来表示算法执行的最好情况的。
大Ω记号和大O记号确定了算法复杂度的上下边界,那么有没有准确估计算法复杂度的记号呢?当然是有的,这种准确估计(就很矛盾)算法复杂度的表示方法称为大θ记号。
不过在日常的计算中,我们更倾向于使用大O记号(人类都是悲观的),但是如果你遇到了大Ω记号和大θ记号,也要记得它们的含义。
好了,概念说了很多,下面我们来尝试计算一些渐进时间复杂度。
计算渐进时间复杂度
在我们了解了复杂度分析的概念和表示方法后,我们尝试着去计算几种常见的时间复杂度。
常数复杂度
常数复杂度是所有算法的终极梦想,因为这种复杂度代表着无论问题规模多大,都能在明确的时间内执行完成。
随便搞一段代码:
public int add(int a, int b) {
int sum = a + b;
return sum;
}
这段代码中,无论a和b输入什么,都只会执行3行代码,这种不随着输入规模而改变执行时间的就是常数级复杂度。
大O记号中表示为:
O
(
1
)
O(1)
O(1)。无论执行几行,只要是能够确定的,都表示为
O
(
1
)
O(1)
O(1)。
线性复杂度
再搞一段代码:
public void add(int n) {
int result = 0;
for (int i = 0; i < n; i++) {
result ++;
}
}
不难看出,这段代码总共会执行
(
1
+
2
n
)
(1+2n)
(1+2n)行代码,那么执行时间也是
(
1
+
2
n
)
(1+2n)
(1+2n)。根据大O记号中的结论,我们可以忽略掉所有的常数,得到的时间复杂度是
O
(
n
)
O(n)
O(n)。
事实上,2n和n的增长趋势是有一定差异的,但整体的变化趋势是随着n的增大而线性增大的,因此我们依旧可以忽略掉常数项和常数系数。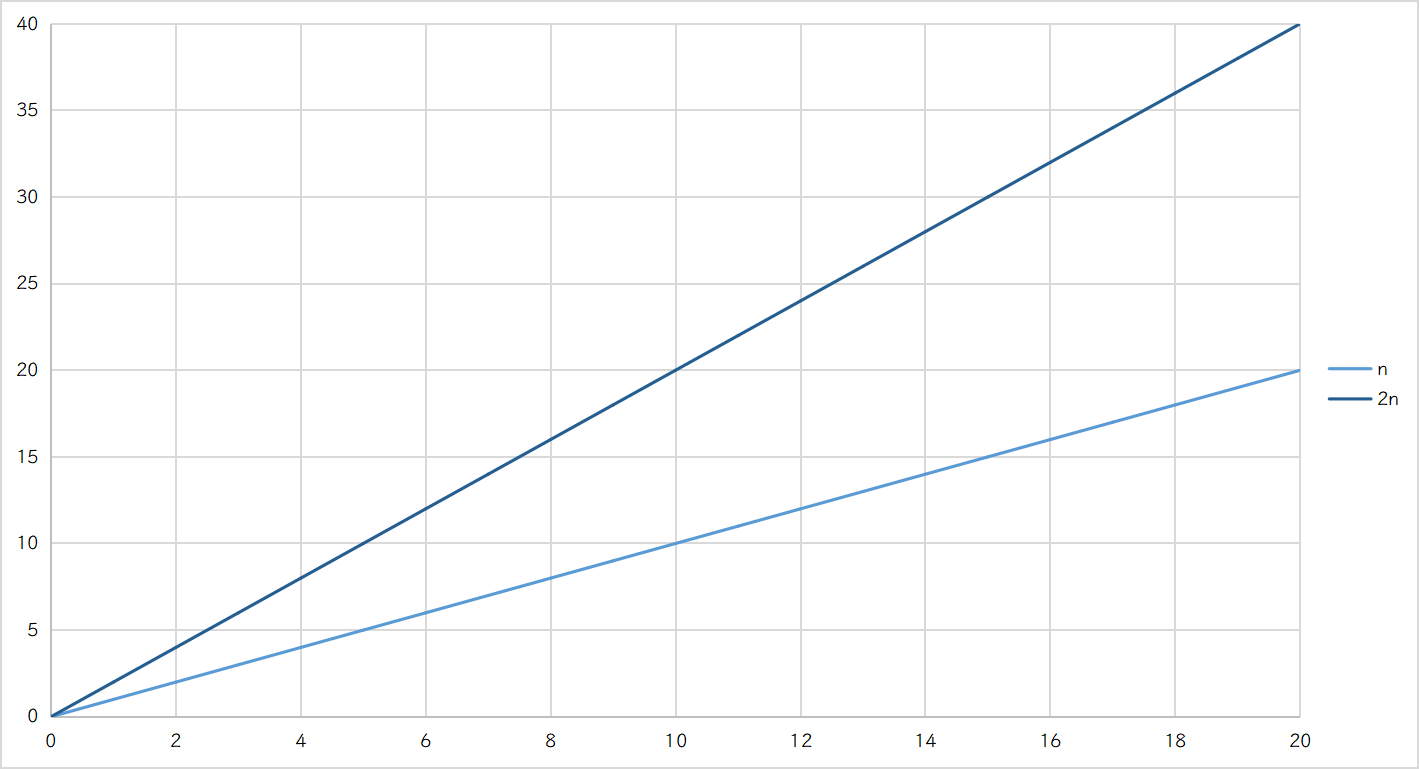
平方复杂度
再再搞一段代码:
public void loop(int n) {
int result = 0;
for (int i = 0; i < n; i++) {
result ++;
}
for (int i = 0; i < n; i++) {
for (int j = 0; i < n; i++) {
result ++;
}
}
}
这段代码的执行次数也是一眼望穿,总共执行
(
1
+
2
n
+
n
+
n
2
)
(1+2n+n+n^2)
(1+2n+n+n2)行,执行时间也是
(
1
+
2
n
+
n
+
n
2
)
(1+2n+n+n^2)
(1+2n+n+n2)。合并后可以得到执行时间是
(
1
+
3
n
+
n
2
)
(1+3n+n^2)
(1+3n+n2),按照大O记号渐进时间复杂度是
O
(
n
2
)
O(n^2)
O(n2)。
我们再来对比下低次项n对整体趋势的影响:
可以看到,在这个级别的复杂度中,低次项n对整体趋势影响已经很小了,因此我们忽略掉低次项,对整体的变化趋势和增长速度影响非常小。
对数复杂度
再再再搞一段代码:
public void multiplication(int n) {
int result = 1;
while (result <= n) {
result = result * 2;
}
}
可以尝试着计算这段代码的时间复杂度,这里需要用上一丢丢的高中数学知识。变量result每次的变化都是原来的2倍,我们可以得到每次循环中result的值如下:
- 第1次: 2 0 2^0 20
- 第2次: 2 1 2^1 21
- 第3次: 2 2 2^2 22
- 第X次: 2 x ≥ n 2x\geq n 2x≥ n
那么我们只需要求解
2
x
=
n
2^x=n
2x=n中x的值即可获得这段代码的时间复杂度。在大O记号下,时间复杂度为
O
(
log
_
n
)
O(\log\_{}{n})
O(log_n)。
我们通过一张函数图像,来看下对数复杂度的增长趋势: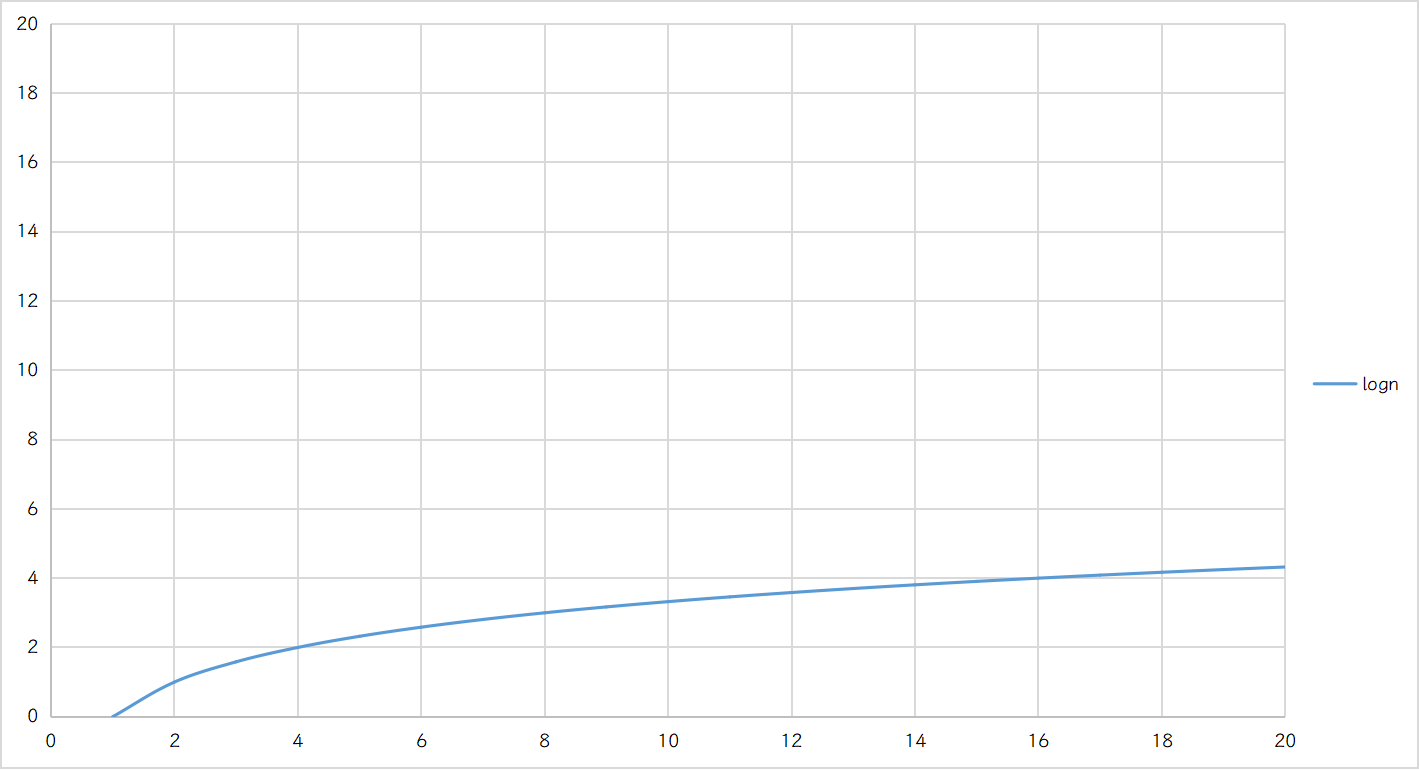
更多复杂度
以上是我们常见的时间复杂度。除此之外还有一些时间复杂度,我们将它们的函数曲线放到同一坐标系中感受下他们的变化趋势: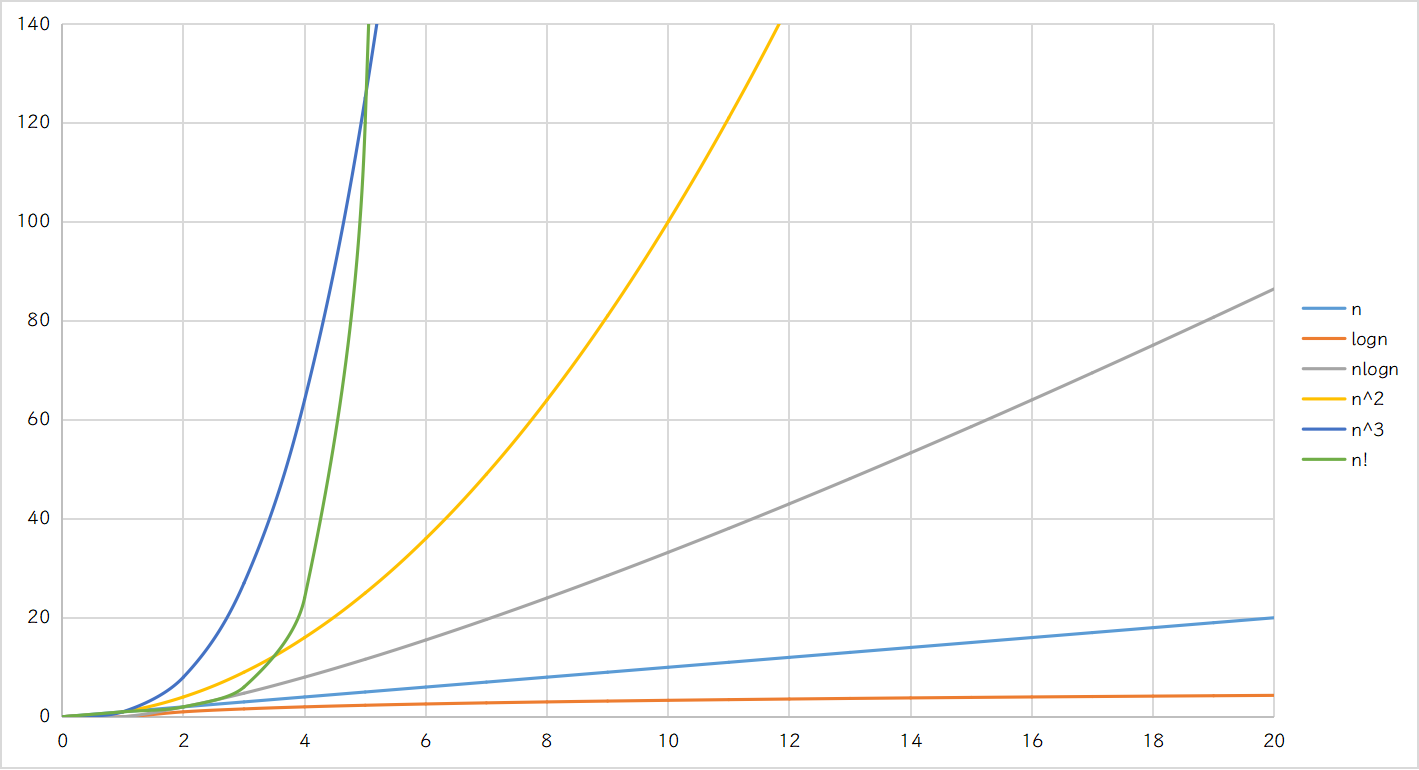
可以看出,除了常数级时间复杂度外,对数级
O
(
log
_
n
)
O(\log\_{}{n})
O(log_n)也是非常理想的状态,这也是我们在设计算法是努力的方向。
最恐怖的是阶乘级复杂度。计算机领域中有一道著名的问题:旅行商问题,它的时间复杂度就是阶乘级的。另外旅行商问题也是NP完全问题。而由NP问题引发的P对NP问题是克雷数学研究所高额悬赏的七个”千禧年难题“之一。
最好,最坏和平均情况
这是今天的最后一段代码了:
public int main(int[] array, int target) {
for(int i = 0; i < array.length; i++) {
if(array[i] == target) {
return i;
}
}
return -1;
}
这段代码的逻辑很简单,循环查找数组中是否存在目标数字,如果存在就返回下标,不存在则返回
−
1
−1
−1。
如果target在首位,那么我们只需要执行一遍循环就可以查找到,此时的时间复杂度是
O
(
1
)
O(1)
O(1)。如果target不在数组中,或者在数组的最后一位,那么需要遍历整个数组,此时的时间复杂度是
O
(
n
)
O(n)
O(n)。
这就是常说的最好情况和最坏情况。
接下来我们来了解下平均情况,还是先来看下邓俊峰老师的解释:
有时也需要考查所谓的平均情况(average case),也就是按照某种约定的概率分布,将规模为n的所有输入对应的计算时间加权平均。
在这段代码中,总共存在
(
n
+
1
)
(n+1)
(n+1) 种情况,其中n种情况是在数组中,1种情况是在数组外,假设每次循环代码的执行时间相同,根据每种情况的概率我们可以得到平均的执行时间为:
1
n
+
1
+
2
n
+
1
+
3
n
+
1
+
…
+
n
−
1
n
+
1
+
n
n
+
1
+
n
+
1
n
+
1
=
1
+
2
+
3
+
…
+
(
n
−
1
)
+
n
+
(
n
+
1
)
n
+
1
=
n
2
+
x
n
+
1
2
n
+
2
\frac{1}{n+1}+\frac{2}{n+1}+\frac{3}{n+1}+…+\frac{n-1}{n+1}+\frac{n}{n+1}+\frac{n+1}{n+1}= \frac{1+2+3+…+(n-1)+n+(n+1)}{n+1}=\frac{n^2+xn+1}{2n+2}
n+11+n+12+n+13+…+n+1n−1+n+1n+n+1n+1= n+11+2+3+…+(n−1)+n+(n+1)=2n+2n2+xn+1
忽略掉所有常数项和常数系数后,我们得到:
n
2
+
n
n
=
1
+
n
\frac{n^2+n}{n}={1+n}
nn2+n=1+n
那么此时我们得到的时间复杂度就是平均情况的时间复杂度,大O记号为
O
(
n
)
O(n)
O(n)。
结语
今天的内容到这里就结束了,我们来回顾下都聊了哪些内容:
今天的主要内容是算法的复杂度分析,解释了算法复杂度分析,渐进分析,大O记号,大Ω记号和大θ记号,其中渐近分析和大O记号是数学概念引申到计算机领域的,因此会有一些数学证明,好在我们的算法和数学比起来还是很简单的,分析起来难度也不是很大。
然后计算了3种常见的渐进时间复杂度,并通过函数曲线展示了其余量级渐进复杂度的变化情况。
练习
最后是一道练习,来自邓俊峰老师的公开课《数据结构》复杂度分析的作业,如下:
x = n;
y = 1;
while(x >= (y-1)*(y-1)) {
y++;
}
请计算以上程序的时间复杂度。
如果本文对你有帮助的话,还请多多点赞支持。如果文章中出现任何错误,还请批评指正。最后欢迎大家关注分享硬核Java技术的金融摸鱼侠[王有志](https://www.yuque.com/wangyouzhi-u3woi/dfhnl0/hqrch62un0cc9sp2?singleDoc# 《🔥快来关注我》),我们下次再见!