RSA是1977年由罗纳德·李维斯特（Ron Rivest）、阿迪·萨莫尔（Adi Shamir）和伦纳德·阿德曼（Leonard Adleman）一起提出的。当时他们三人都在麻省理工学院工作。RSA就是他们三人姓氏开头字母拼在一起组成的。

        RSA是非对称算法，加密密钥和解密密钥是不一样的，或者说不能由其中一个密钥推导出另一个密钥。RSA密钥尺寸大，加解密速度慢，一般用来加密少量数据，比如DES的密钥。非对称加密为数据的加密与解密提供了一个非常安全的方法，它使用了一对密钥，公钥（public key）和私钥（private key）。私钥只能由一方安全保管，不能外泄，而公钥则可以发给任何请求它的人。非对称加密使用这对密钥中的公钥进行加密，而解密则需要私钥。

数学概念：

        质数：质数又称素数。一个大于1的自然数，除了1和它自身外，不能被其他自然数整除的数叫做质数；否则称为合数（规定1既不是质数也不是合数）。

        因子：例如：2X3=6 那么2和3就是6的因子

        % ：代表取余，例如5%2=1  

算法原理：

       两个质数：P、Q 一般非常大，取值没有限制

       函数T： 函数T=(P-1)*(Q-1)

       质数的乘积N=P*Q 

       公钥参数E（也是质数）条件：1<公钥<T; 且不是T的因子  取值自选

       私钥参数D  条件：(DXE)%T=D  取值自选

密钥生成

公私密钥生成：

假设取P=3、Q=11  实际运用的时候选的很大

N=P X Q= 3 X 11 = 33   精髓：哪怕知道N，也很难算出P和Q

T=（P-1）X（Q-1）=20

E=3    #这里的3是根据上面的规则选的其中一个

D=7    #这里的7符合上面的规则

公钥（3、33）   

私钥（7、33） 

这样一对密钥就生成了。

加解密举例

        

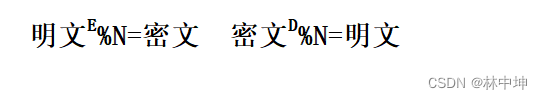
        假设明文内容是：5  #取简单的方便计算

        加密就是：（5X5X5）%33=26   26就是密文

        解密就是：(26X26X26X26X26X26X26)%33=5   5就是明文

核心思想：只要不知道私钥D就无法破译，而得到D需要依靠T，T是P、Q得到的，由于P、Q都是很大的质数，所以很难算出对应的P和Q。