二叉树里的双指针
所谓的双指针就是定义了两个变量,在二叉树中有需要至少定义两个变量才能解决问题。这两个指针可能针对一棵树,也可能针对两棵树,姑且也称之为“双指针”。这些问题一般与对称、反转和合并等类型题相关。
判断两棵树是否相同
100. 相同的树 - 力扣(LeetCode)
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:

输入:p = [1,2,3], q = [1,2,3]
输出:true
示例 2:
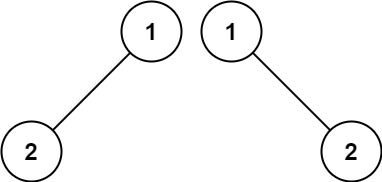
输入:p = [1,2], q = [1,null,2]
输出:false
示例 3:
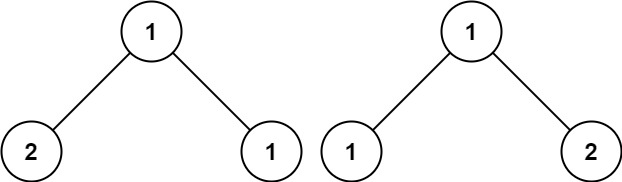
输入:p = [1,2,1], q = [1,1,2]
输出:false
提示:
- 两棵树上的节点数目都在范围
[0, 100]内 -104 <= Node.val <= 104
同时进行前序遍历
两个二叉树同时进行前序遍历,先判断根节点是否相同, 如果相同再分别判断左右子树是否相同,判断的过程中只要有一个不相同就返回 false,全部相同才会返回true。
public boolean isSameTree(TreeNode p, TreeNode q)
{
//如果结点都为null,则认为两个结点相同
if(p == null && q == null)
return true;
//经过前面的判断,到这里要么p、q都不为null,要么p、q中只有一个为null
//若p、q一个为null一个不为null,则认为两棵树不相同
if(p == null || q == null)
return false;
//若结点值不同,则认为两棵树不相同
if(p.val != q.val)
return false;
//该结点没问题,接下来对该结点的左右子树进行对比分析
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
}
对称二叉树
101. 对称二叉树 - 力扣(LeetCode)
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
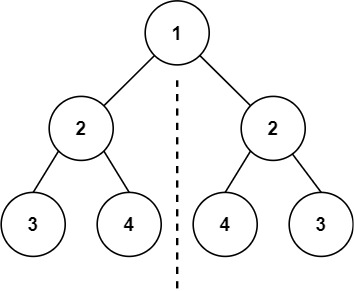
输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:
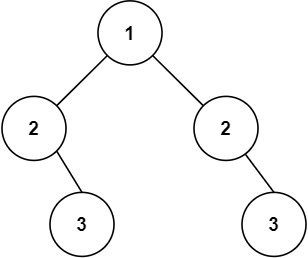
输入:root = [1,2,2,null,3,null,3]
输出:false
提示:
- 树中节点数目在范围
[1, 1000]内 -100 <= Node.val <= 100
递归
若根结点的左右节点都不为 null 且 val 相同。
- 比较外侧是否对称:传入的是左节点的左孩子,右节点的右孩子。
- 比较内侧是否对称:传入的是左节点的右孩子,右节点的左孩子。
- 有一侧不对称就返回false ,左右都对称则返回true 。
//主方法
public boolean isSymmetric(TreeNode root)
{
return check(root.left, root.right);
}
public boolean check(TreeNode p, TreeNode q)
{
if (q == null && p == null)
return true;
if(q == null || p == null)
return false;
if(q.val != p.val)
return false;
return check(p.left ,q.right) && check(p.right, q.left);
}
合并二叉树
617. 合并二叉树 - 力扣(LeetCode)
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。
合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
示例 1:
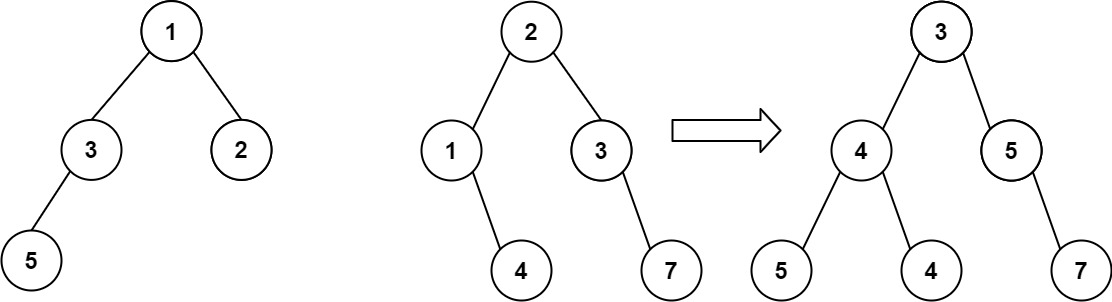
输入:root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出:[3,4,5,5,4,null,7]
提示:
- 两棵树中的节点数目在范围
[0, 2000]内 -104 <= Node.val <= 104
解
合并得到某个节点之后,还要对该节点的左右子树分别进行合并
public TreeNode mergeTrees(TreeNode root1, TreeNode root2)
{
//触底时返回 null 或者不为 null 的那个结点
if (root1 == null)
return root2;
if (root2 == null)
return root1;
//两个结点均不为 null 则进行合并,生成一个新结点(显性合并)
TreeNode mergeNode = new TreeNode(root1.val + root2.val);
//合并两个结点的左子树,然后衔接到新结点上
mergeNode.left = mergeTrees(root1.left, root2.left);
//合并两个结点的右子树,然后衔接到新结点上
mergeNode.right = mergeTrees(root1.right, root2.right);
return mergeNode; //返回合并后的新结点
}
路径专题
二叉树的所有路径
257. 二叉树的所有路径 - 力扣(LeetCode)
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
示例 1:
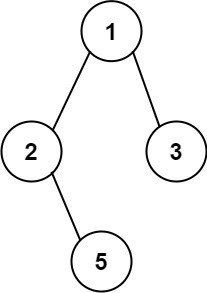
输入:root = [1,2,3,null,5]
输出:["1->2->5","1->3"]
示例 2:
输入:root = [1]
输出:["1"]
提示:
- 树中节点的数目在范围
[1, 100]内
前序遍历+ list
调整一下对结点的处理操作即可
public List<String> binaryTreePaths(TreeNode root)
{
ArrayList<String> list = new ArrayList<>();
preOrder(root, list, "");
return list;
}
public void preOrder(TreeNode root, List<String> list, String ans)
{
if (root == null)
return;
//找到一个叶子结点后,将路径添加到列表,返回
if (root.left == null && root.right == null)
{
ans = ans + String.format("%s",root.val);
list.add(ans);
return;
}
//保存路径上的节点
ans = ans + String.format("%s->",root.val);
preOrder(root.left, list, ans);
preOrder(root.right, list, ans);
}
二叉树的路径总和
112. 路径总和 - 力扣(LeetCode)
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
示例 1:
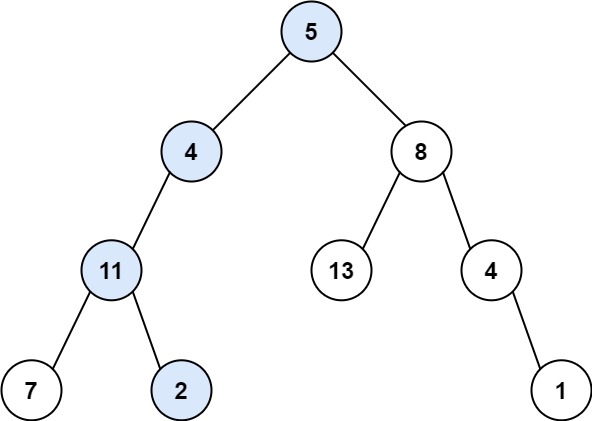
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
解释:等于目标和的根节点到叶节点路径如上图所示。
示例 2:
输入:root = [], targetSum = 0
输出:false
解释:由于树是空的,所以不存在根节点到叶子节点的路径。
提示:
- 树中节点的数目在范围
[0, 5000]内
前序遍历 + list
本来想着用一个 boolean 类型的 flag 标记一下即可,但发现即使找到答案路径后,flag 在往后的递归中也会受到影响而改变结果,于是不得已用了一个列表来标记(似乎列表才属于循环不变量、递归不变量)
public boolean hasPathSum(TreeNode root, int targetSum)
{
ArrayList<Boolean> list = new ArrayList<Boolean>();
preOrder(root,list,0, targetSum);
return !list.isEmpty();
}
public void preOrder(TreeNode root, ArrayList<Boolean> list, int sum, int targetSum)
{
if (root == null)
return;
//在叶子结点处进行判断,然后返回
if (root.left == null && root.right == null)
{
sum = sum + root.val;
if(sum == targetSum)
list.add(true);
return;
}
//计算路径上非叶节点的和
sum = sum + root.val;
preOrder(root.left, list, sum, targetSum );
preOrder(root.right, list, sum, targetSum);
}
递归地询问子节点是否满足条件
若当前节点就是叶子节点,则直接判断 val 是否等于 targetSum;若当前节点不是叶子节点,则递归地询问它的两个子节点是否满足条件 val == targetSum - 父节点.val ,有一个满足即返回 true,两个都不满足则返回 false (子节点为 null 视为不满足)。
public boolean hasPathSum(TreeNode root, int targetSum)
{
if (root == null)
return false;
if (root.left == null && root.right == null)
return root.val == targetSum;
boolean left = hasPathSum(root.left, targetSum - root.val);
boolean right = hasPathSum(root.right, targetSum - root.val);
return left || right;
}
翻转二叉树
226. 翻转二叉树 - 力扣(LeetCode)
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
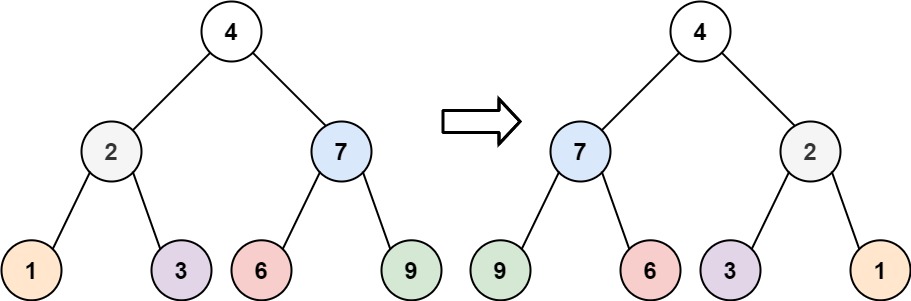
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
递归
递归地翻转当前结点的两个子节点即可
public TreeNode invertTree(TreeNode root)
{
if (root == null)
return null;
TreeNode t = root.left;
root.left = root.right;
root.right = t;
invertTree(root.left);
invertTree(root.right);
return root;
}
层次遍历
public TreeNode invertTree(TreeNode root)
{
if (root == null)
return null;
ArrayDeque<TreeNode> queue = new ArrayDeque<>();
queue.offer(root);
while (!queue.isEmpty())
{
TreeNode curNode = queue.poll();
TreeNode t = curNode.left;
curNode.left = curNode.right;
curNode.right = t;
if (curNode.left != null)
queue.offer(curNode.left);
if (curNode.right != null)
queue.offer(curNode.right);
}
return root;
}