章节知识点分析
第一章绪论
基本概念
-
数据
-
数据元素(记录、表目,是数据集合中一个个体)
-
数据项:一个数据元素可由若干数据项组成
-
数据对象:性质相同的数据元素的集合,是数据的一个子集
-
数据结构:带结构的数据元素集合
- 包括(D:元素集合、S:D上的关系、Op:D上的运算)
-
逻辑结构:数据元素之间的逻辑关系,与计算机无关
- 包括(D,S)
四种基本的逻辑结构:
- 集合结构
- 线性结构
- 树形结构
- 图状结构
- 存储结构(物理结构):指数据的逻辑结构在计算机存储器中的映像表示。
- 用二进制位串表示数据元素。元素映像叫结点,数据项映像叫数据域。
四种不同的存储结构
- 顺序存储结构
- 链式存储结构
- 哈希存储结构
- 索引存储结构
- 算法:建立在数据结构基础上的、求解问题的一系列确切的步骤
- 五个特性:有穷性、确定性、可行性、输入、输出
- 性能指标:正确性、可读性、健壮性、高效率与低存储需求
- 事前估计:空间复杂度、时间复杂度
- 时间复杂度有最坏、最好、平均等。
- 原地算法:空间复杂度O(1)、存储密度:数据本身存储量/实际所占存储量
题型
- 基本概念的填写
- 复杂度分析
第二章线性表(线性逻辑结构)
线性表:在数据元素的非空有限集中
- 数据元素在表中的位置只取决于其序号
- 除第一个和最后一个、每个数据元素均只有一个前驱和后驱。存在唯一第一个和最后一个
基础是用顺序表存储(存储结构)。

单链表(存储结构)
注意区分有无头结点的情况
当无头结点时,考虑是否需要对头元素做特殊处理
- 单循环链表:最后一个的尾指针是第一个(或空表头)
- 双向链表:也可是双向的循环

静态链表用数组模拟链表,逻辑上像链表,物理上看是数组。
采用结构体创建带数据域和指针域(整数)的结构,使用这种结构构成数组。
题型
主要是一些实现特定操作的算法题
第三章栈与队列(逻辑结构)
-
栈:先进后出(栈顶top、栈底bottom、入栈出栈push\pop)
-
栈也可以由顺序存储结构或链式存储结构实现(不同的存储结构)
-
八股:n个元素依次入栈,最多可以得到的合法序列数 ( 2 n ) ! / [ ( n + 1 ) ! ∗ n ! ] (2n)!/[(n+1)!*n!] (2n)!/[(n+1)!∗n!]
-
应用:递归算法(保存现场变量)、整数表达式求值
-
队列:先进先出
-
链式可以是循环队列、逻辑上的优化可以是双端队列。
题型
- 递归相关计算
- 操作合法性、出入序列合法性
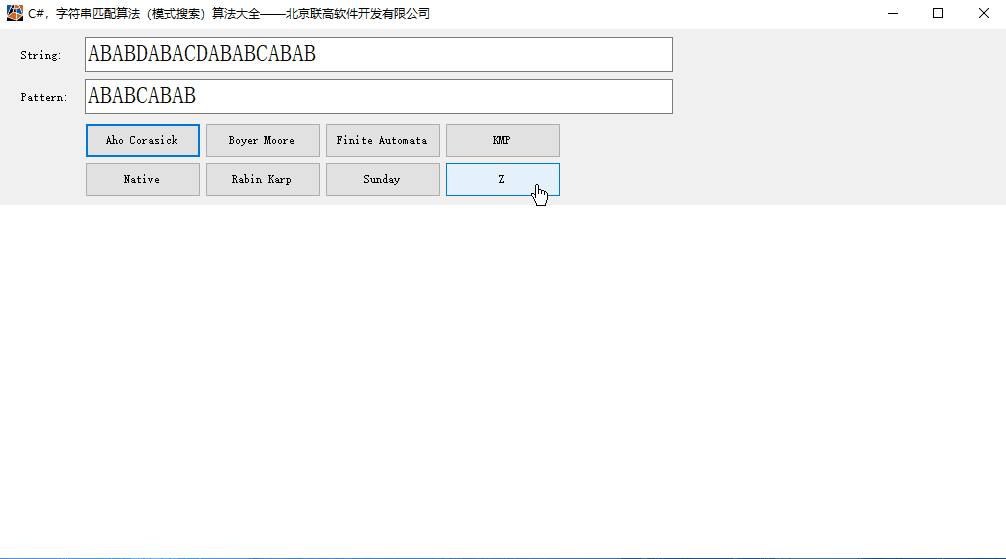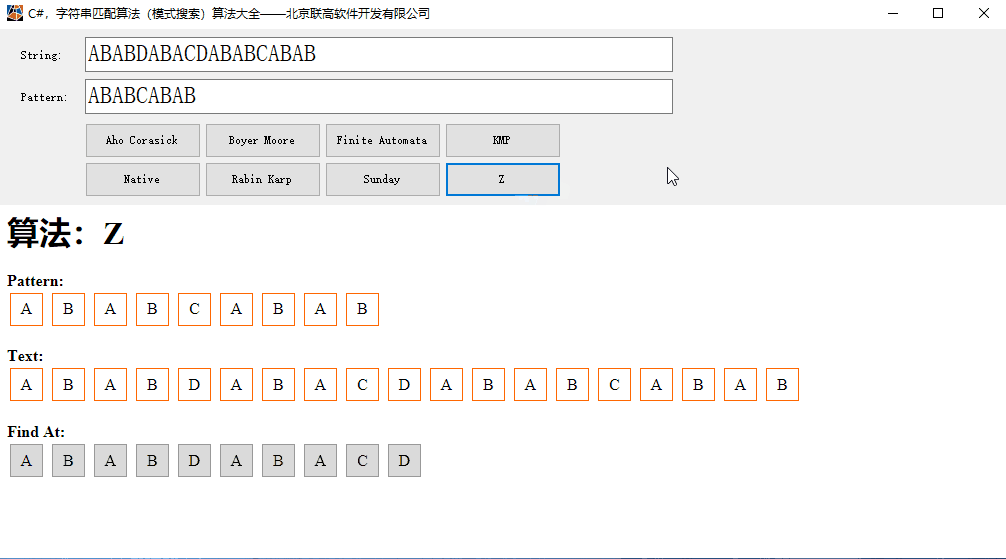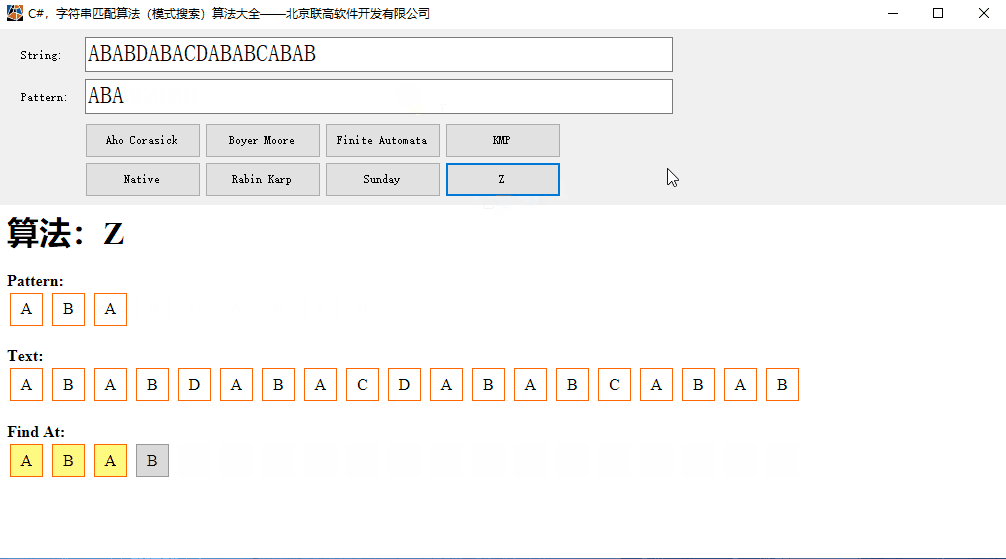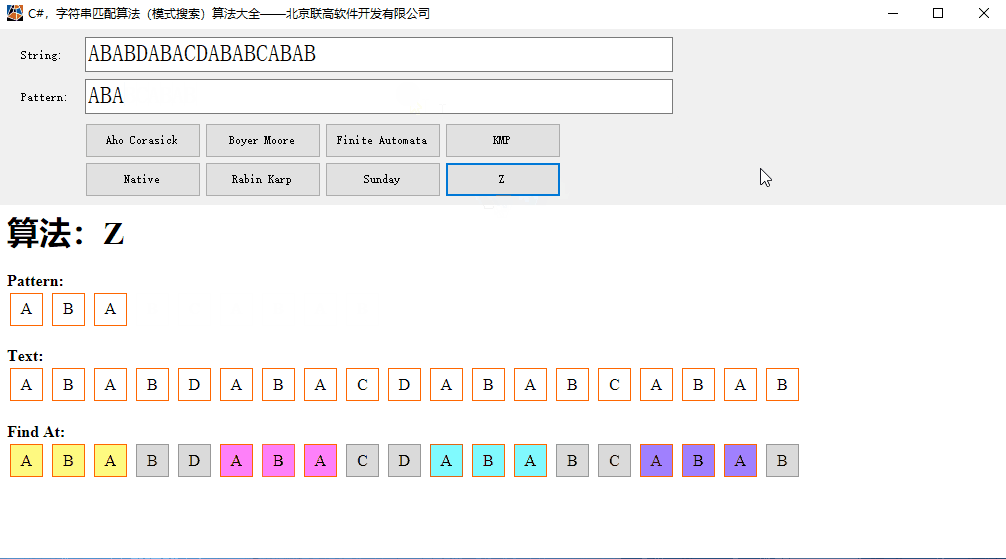
第四章字符串和模式匹配
- 存储
- 静态就是数组存储
- 动态就是申请空间或链式结构存储
- 模式匹配
- 目标:原始串、模式:需要找到的子串、结果:第一次匹配到的位置
KMP算法
复杂度:(m+n)
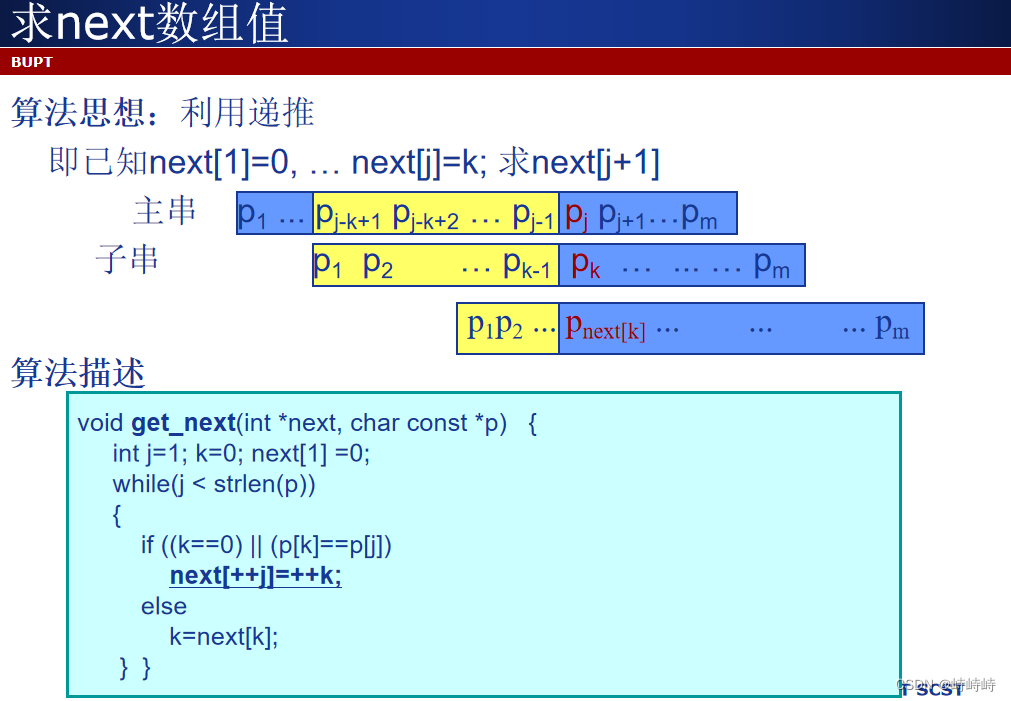

KMP算法思想
当模式串j位成功匹配或j=0时,i j同时自增,否则j回退到next[j]记录的位置,重新比较。
next数组求解
k=0或当前位置能匹配上,下一个位置记录k+1,否则k回溯到next[k]
修正
对于next数组的修正,若当前位置可以匹配,本来是直接填写下一个位置的值的,但现在需要检查下一个位置的值是否和k位置相同,若相同则填写next[k]的值,不直接写k
题型
模拟KMP算法求Next数组,注意记录关键点在于时刻明确k的值。
第五章数组和广义表
数组本质上就是线性表,下标有确定的转化关系
矩阵的压缩存储
-
对称矩阵

-
带状矩阵
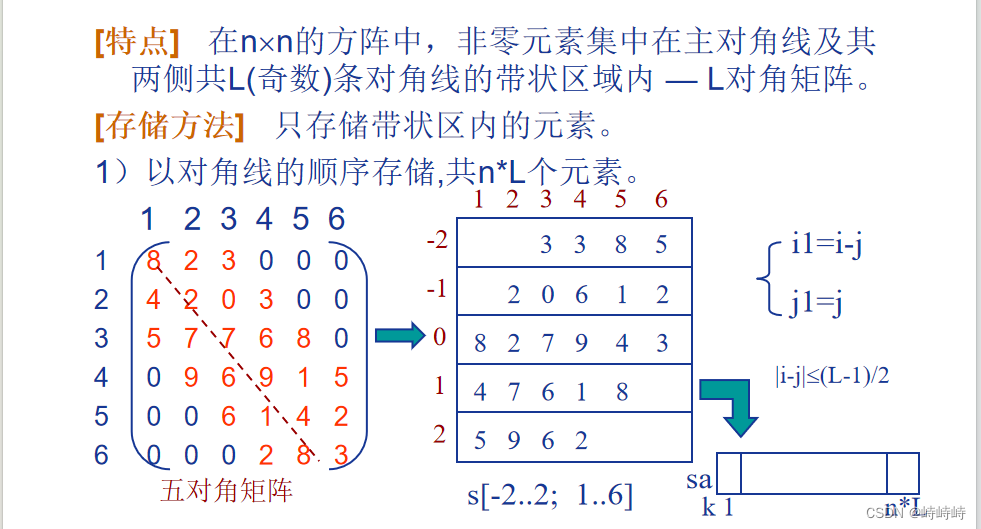
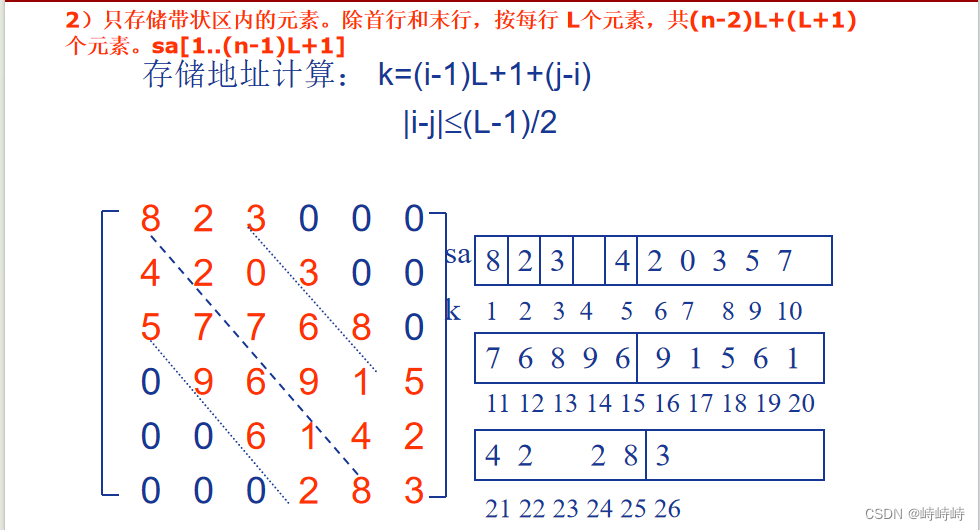
以对角线元素为中心,其确定每行中心位置,同行元素按照原来的相对中心的位置分布。
- 稀疏矩阵
-
三元组表

-
十字正交链表
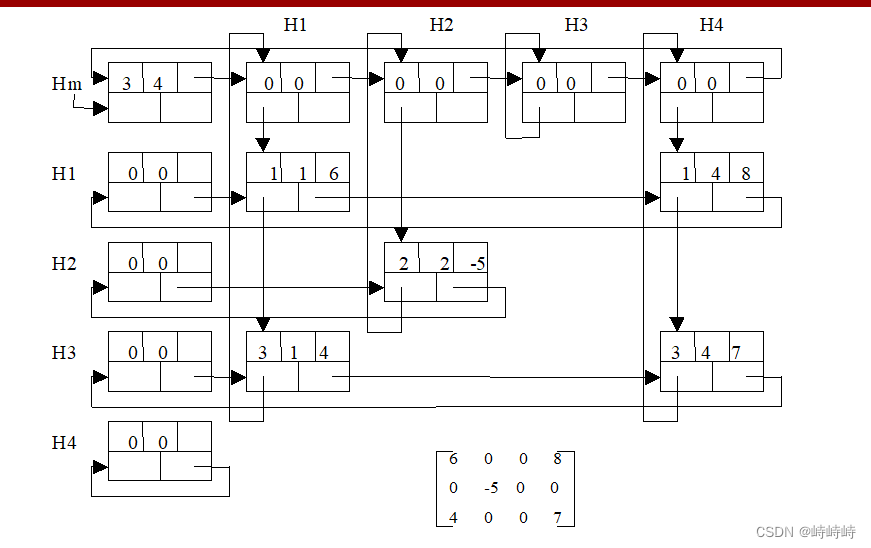
-
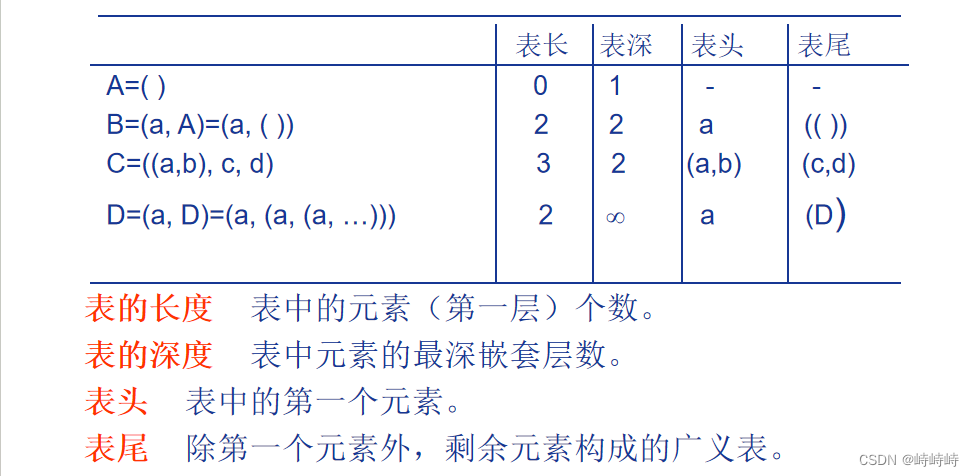
广义表
广义表的定义是递归的
注意表头表尾是一对相对概念。
正常情况下只有取表头能取出原子。
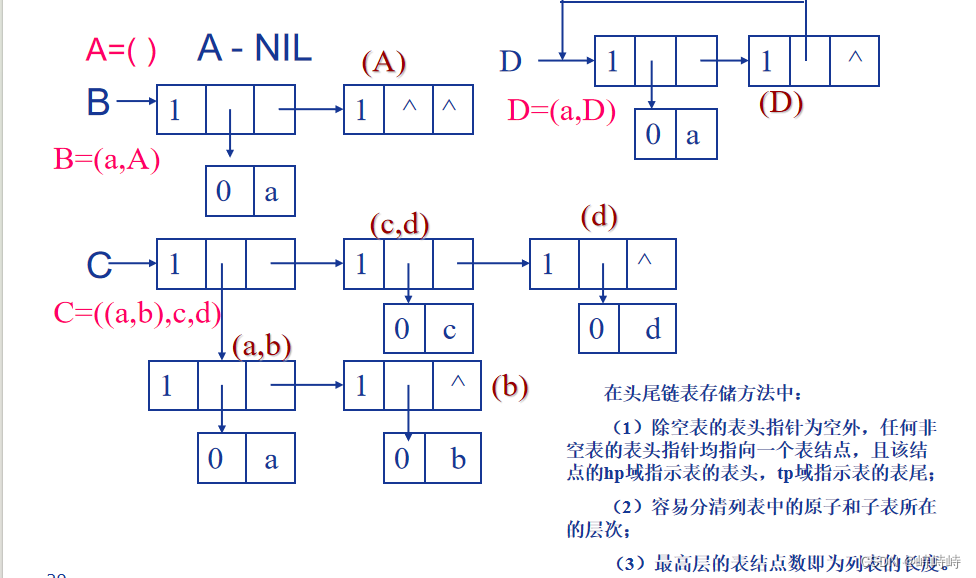
存储方式一:表头表尾分法
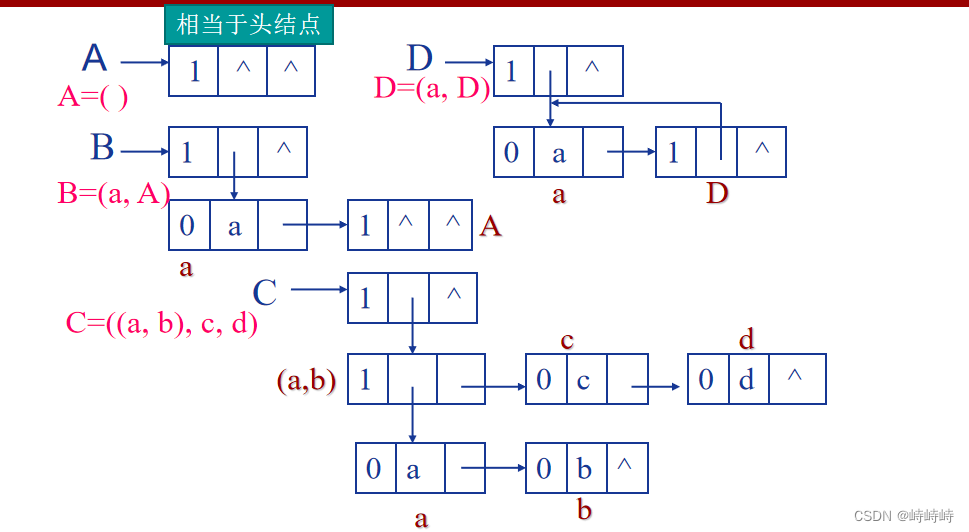
存储方式二:孩子兄弟兄弟分法(扩展的线性链表)
题型
- 矩阵压缩下角标对应关系、三元组表或十字链表表示
- 广义表取表头表尾、相关操作(递归)
- 取头、取尾、求长度、深度等
- 头尾链表存储形式、扩展的线性链表形式
第六章树与二叉树

度之和==结点数之和+1
完全二叉树中,双亲和左右孩子的序号有明确对应关系2i 2i+1
消除尾递归:想办法把尾递归改成迭代形式。
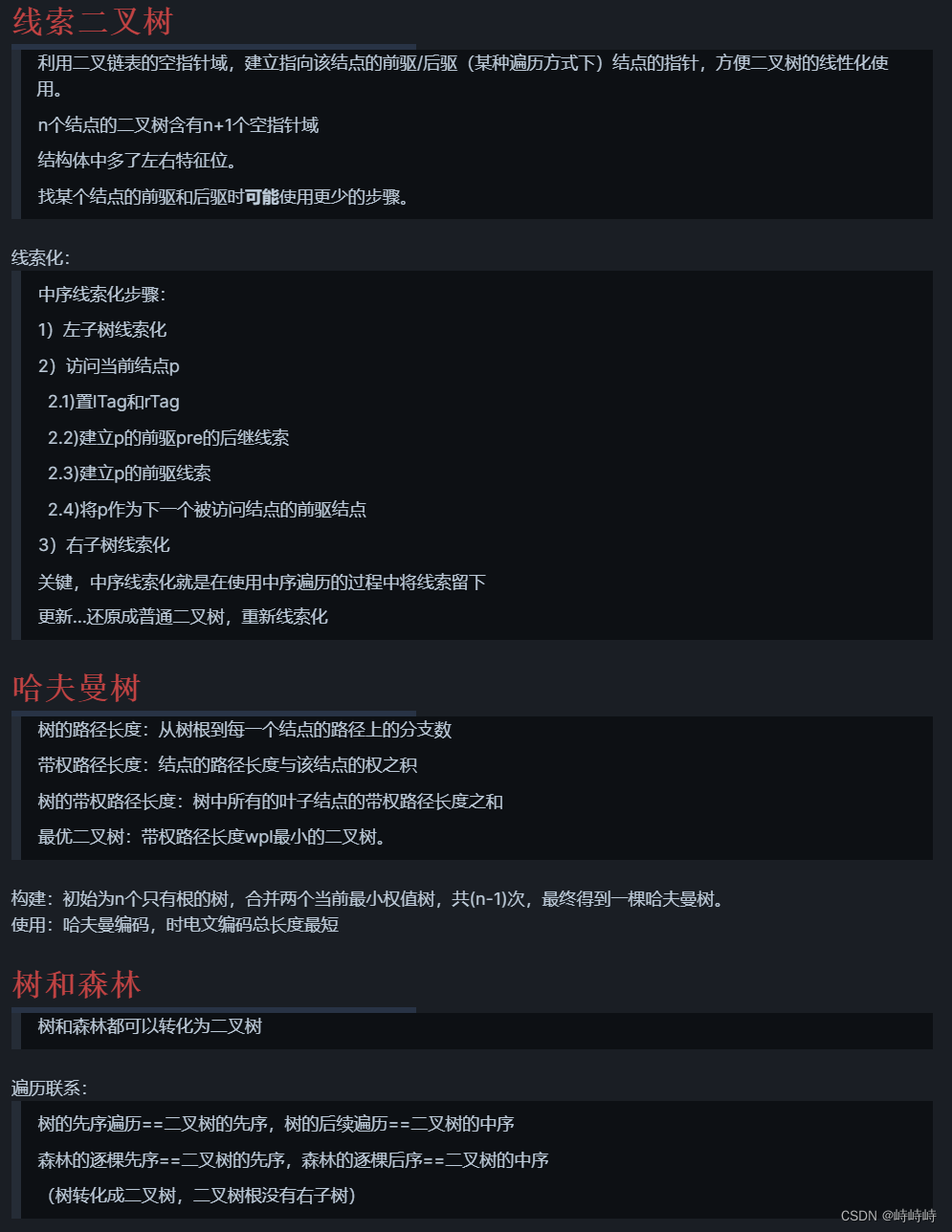
WPL:带权路径长度之和。使WPL最小的数是哈夫曼树树。(路径长度是层数减1,根层数为1)
哈夫曼不等长,是前缀编码,没有度为1的结点。结点总数为2n-1
树转化为二叉树:根无右子树,左支是孩子,右支是兄弟。树/森林的先、后序对应二叉树的先、中序。
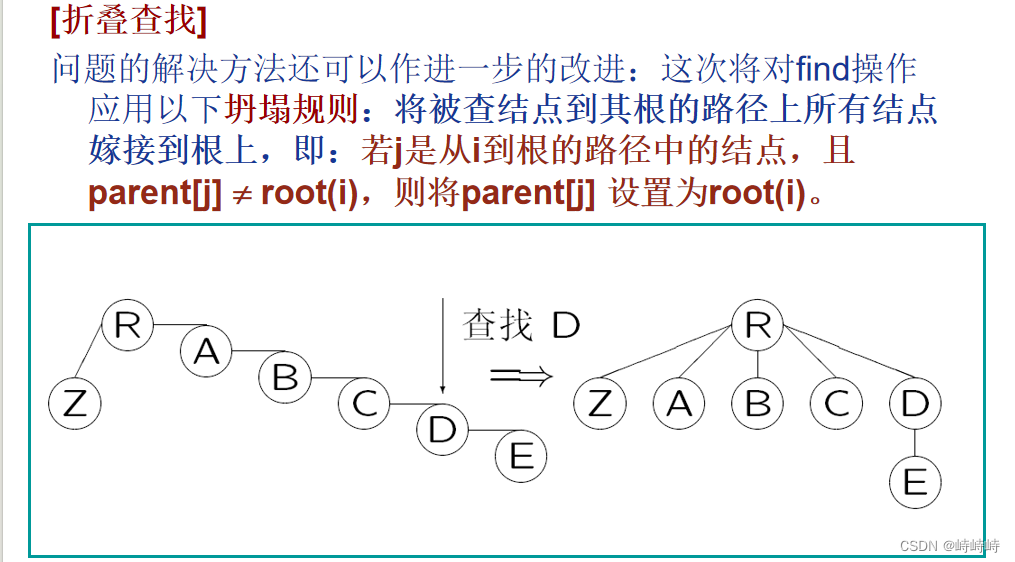
并查集,互不相交的集合。
使用树或数组表示。通常包括合并和查找操作。(通常选出一个代表做根)
合并时,为了防止退化树的出现,通常使用加权合并的方式(结点数大的做双亲)。
题型
- 树的遍历序、树的相关算法
- 并查集相关操作。
第七章图
图的基本概念
- 顶点
- 无向图、有向图
- 权、网(边、弧带权的图)
- 邻接:顶点间关系、关联:边关联于两个顶点
- 子图、生成子图:由图的全部顶点和部分边组成
- 度
- 路径、回路、简单路径、简单回路(加上简单后,除起点和终点外其它点不同)
- 连通图:无向图中,任何一对顶点间都存在路径
- 强连通分量:无向图中的极大连通子图 (加强说明对应有向图范畴)
- 生成树:包含全部顶点的极小连通子图
图的存储结构
- 邻接矩阵:矩阵
(i,j)表示i-j的路径 - 邻接表:顶点数组+边链表
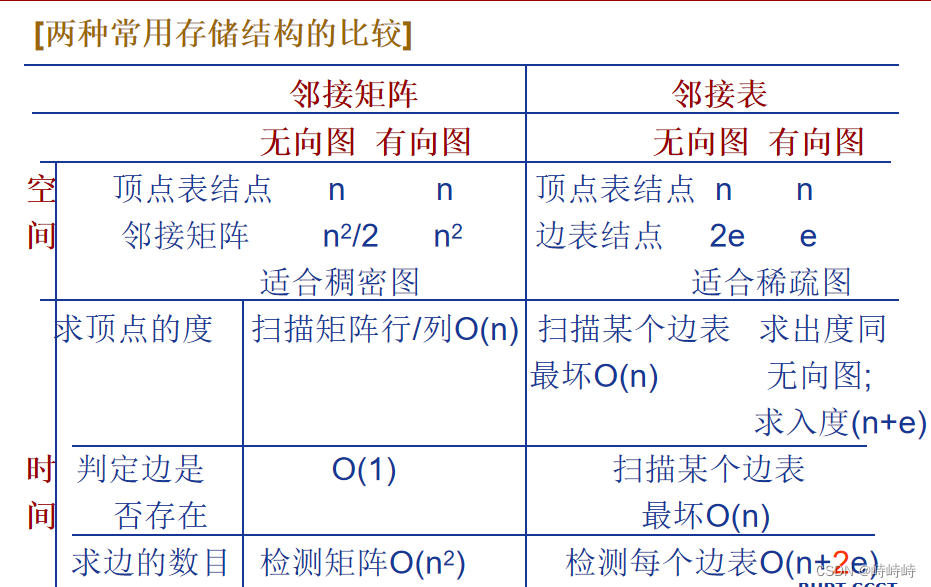
- 关联矩阵:定点数*边数的矩阵
- 十字链表:同时有指向入边集合和出边集合的链
- 邻接多重表
图的遍历
深度优先和广度优先(每个顶点只能访问一次)
对于图而言,深度优先遍历可以判断其是否有环。
图的联通性
一个图的生成树不唯一,一般广度优先生成树的高度更小。
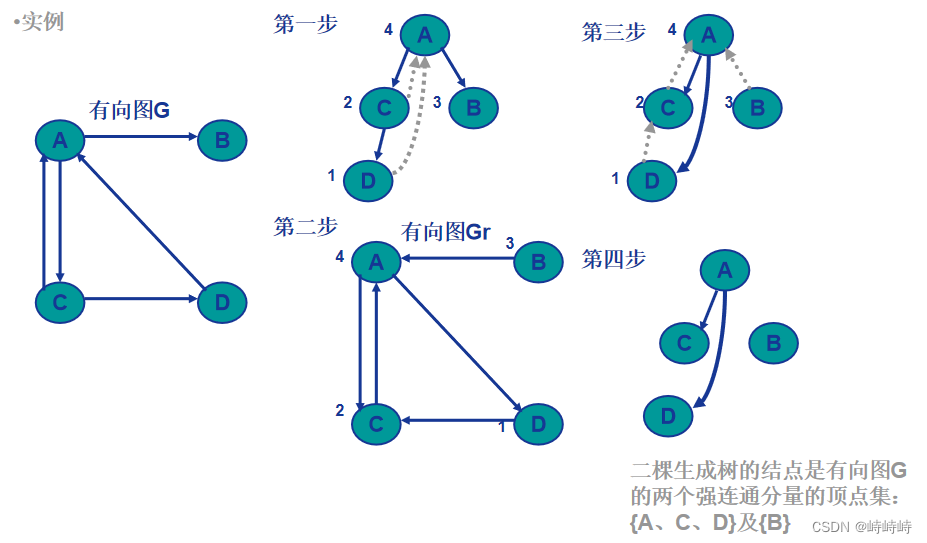
强连通分量求法
深搜+逆序编号
反边+按编号从大到小深搜,每一次新开的搜索集合属于同一个强连通分量。
最小生成树
Prim算法:(在不形成环的基础上),每次挑出以连通部分到未连通部分最小的边。
Kruskal算法:在不形成环的基础上,每次挑出所有边中最小的一个加入。
有向无环图的应用
有向无环图DAG:AOV网络:表示活动执行次序;AOE网络:有向边定义活动进行所需时间
拓扑排序:每次取出入度(出度)为0的顶点。
当使用深搜实现时,要注意只适用于有向无环图。
关键路径:AOE网中,进入顶点v的事件全部发生,v才可以开始。
关键路径长度==最短工期。
关键路径加快可以缩短工期
- 步骤一:求所有事件(顶点)发生的最早时间(依赖于拓扑排序,按照排序结果依次求解)
- 步骤二:求所有事件发生的最迟时间(先设置为最早时间,再遍历所有后继邻接点,找到最迟时间。依赖于逆向拓扑排序,按照逆向拓扑排序顺序依次求解)
- 步骤三:根据事件(顶点)的最早开始和最迟结束时间。计算每条边的最早开始和最迟开始时间,二者相等的为关键路径上的边。
注意前两步是利用拓扑排序求出顶点的最早和最迟时间。第三步需要求边的最早开始和最迟开始时间。也就是起点的最早和(终点最迟-边长)
最短路径
问题对象:有向网络
典型问题:单源最短路径:迪杰斯特拉、贝尔曼福德
多源:弗洛伊德、Johnson
迪杰斯特拉:按路径长度递增(以连通集合出发的边)依次产生个顶点最短路径。(不断松弛未确定的点集距离)
Floyd:二维矩阵存距离,依次增加可供做桥梁的中间点集。
第八章查找
基本概念和术语
平均查找长度:ASL=所有记录查找的概率和比较次数乘积之和
-
顺序表查找

-
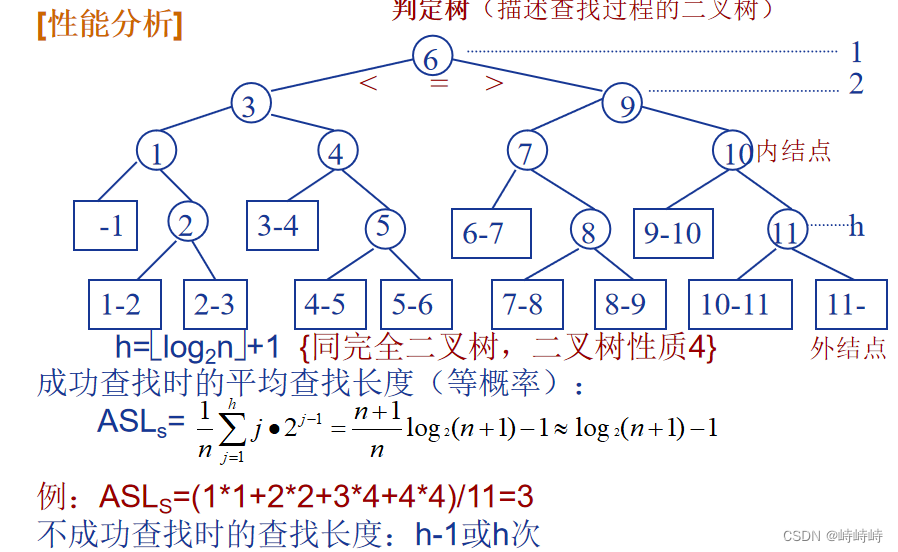
二分查找(注意ASL求法)
-
静态树的查找
类似二分,构造成树的样子,每次和根比较后,就可以确定在左子树或是在右子树。
静态最优查找树:带权内路径长度之和最小。(与ASL成正比)
次优查找树,构造开销更小。通过找到使两侧概率和尽可能相等的元素为根。 -
分块查找
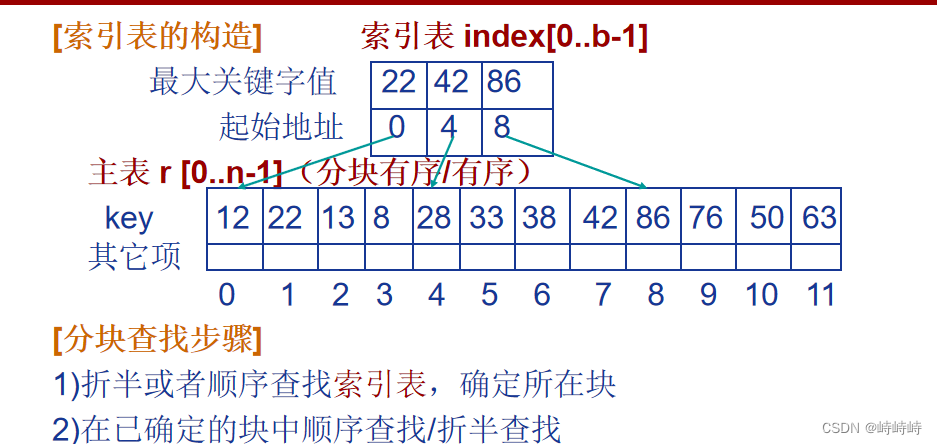
每块中记录个数为根号n时,ASL最小=根号n+1。
-
二叉排序树
-
平衡二叉树
-
B树
-
哈希表
第九章内部排序
基本概念和术语
- 插入排序
- 交换排序
- 选择排序
- 并归排序
- 基数排序
算法比较
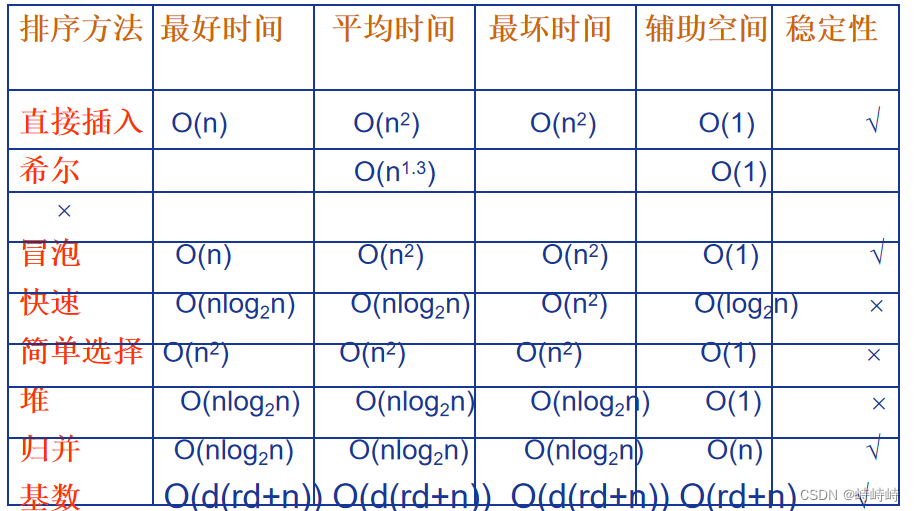
关键例题

第十章外部排序
- 并归排序
- 多路平衡并归
- 置换-选择排序
- 磁盘排序
例题