关于CNN卷积神经网络与Conv2D标准卷积的重要概念

温故而知新，可以为师矣！

一、参考资料

深入解读卷积网络的工作原理（附实现代码）
深入解读反卷积网络（附实现代码）
Wavelet U-net进行微光图像处理
卷积知识点
CNN网络的设计论：NAS vs Handcraft

二、卷积神经网络(CNN)相关介绍

1. CNN网络简介

1.1 CNN特征提取

学习输入到输出的映射，并对映射关系加以训练，训练好的模型也具备了这种映射能力。浅层网络一般学习的是边缘、颜色、亮度等，较深层网络学习的是纹理，而更深层的网络学习的是具有一些辨识度的特征，所以卷积神经网络学习的特征逐渐抽象到更高级别。

1.2 CNN网络优点

参数共享。对输入图像进行卷积操作时，对不同的区域都会共享同一个卷积核，即共享同一组参数，使得网络的参数量才会大大减少；
稀疏性连接。进行卷积操作之后，输出图像的任何一个区域只跟输入图像的一部分有关。

2. CNN网络结构

CNN网络一般由输入层、卷积层(convolution layer)、激活层、池化层(pooling layer)和全连接层(fully-connected layer，FC layer)五部分组成。其中，最核心的层包括：

convolution layer：提取spacial information；
pooling layer：降低图像或特征图分辨率，减少运算量并获得semantic information；
FC layer：回归目标。

注意：随着时代的改变，虽然pooling layer时常被较大stride的convolution取代，global average pooling 与1x1 convolution也时不时代替了 FC layer，这个大思路依然是大致没变的。

3. 卷积层

如果没有特殊说明，卷积指的是标准卷积(Conv2D)，卷积操作指的是标准卷积的正向卷积过程。

卷积层功能：一张图像在计算机中自动识别为一个二维矩阵。卷积层对输入图像进行特征提取，其内部是由多个卷积核组成的，多个卷积核构成滤波器。

卷积层参数：卷积核大小、步长和填充方式。

卷积层重要特性：权值共享。对于任意一张图像，用一个滤波器按照先横后竖的顺序去覆盖这张图，因为这张图像的每个区域都是被同一个滤波器覆盖，所以各个区域的权重一样。

多卷积层：一层卷积学到的特征往往是局部的，而卷积层数越多，学到的特征就越全局化。实际应用中，往往使用多层卷积，然后再使用全连接层进行训练。

3.1 卷积核(kernel/filters)

kernel称为卷积核，filters称为滤波器，多个kernel构成filters。卷积核的数量，也就是卷积核通道数。例如，卷积核的尺寸为： $K * K * 3 * M$ ，单个卷积核尺寸为： $K * K * 3$ ，卷积核的数量为： $M$ ，即表示通道数。

在TensorFlow中叫filters，在keras中叫kernel，不同文献有不同的叫法，在这里统一叫做卷积核kernel，一般kernel的大小(height*width)为1X1，3X3，5X5，7X7。

卷积核与特征（特征图）的关系：不同的卷积核可以提取不同的特征，一个卷积核只能提取一种特征，32个卷积核就可以提取32种特征。通过卷积操作，一个卷积核对应输出一维特征图，多个卷积核对应输出多维特征图，维度也称为特征图的深度，即对应特征图通道数。
在这里插入图片描述

3.2 卷积操作

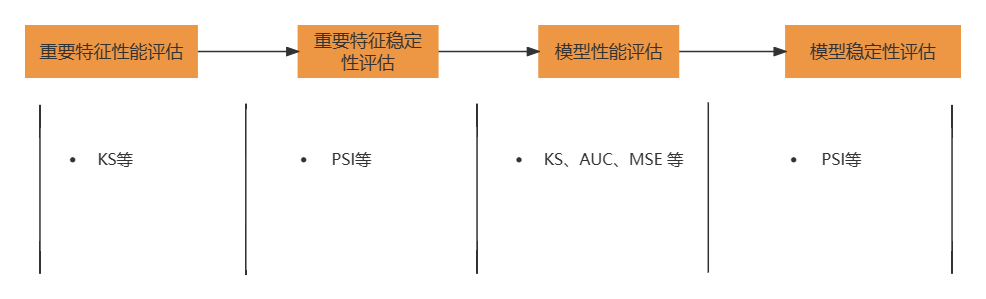
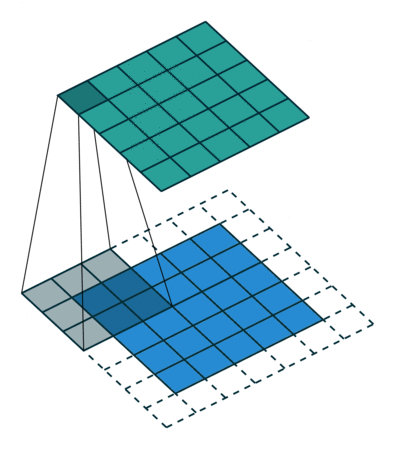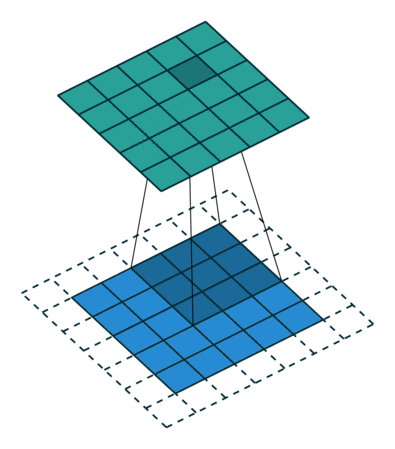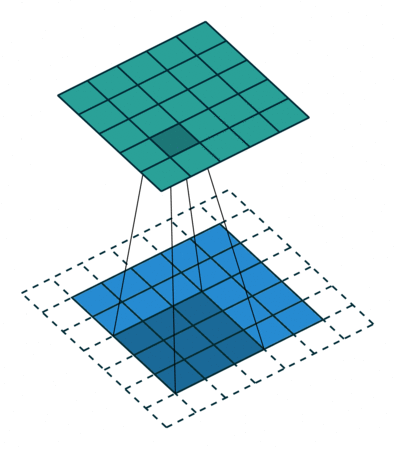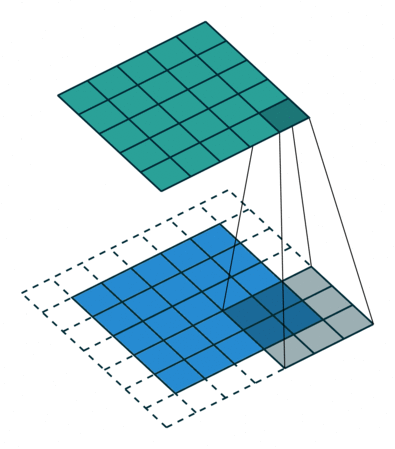
卷积操作是基于卷积的数学运算，可以将卷积核看成一个二维数字矩阵，输入图像与卷积核进行卷积后就得到了特征图。先在输入图像的某一个区域覆盖卷积核，然后将卷积核中的每一个数值与输入图像相应位置像素的数值相乘，把乘积累加起来，得到的和便是输出图像对应位置中目标像素的数值，多次重复此操作直到输入图像中所有区域被卷积核覆盖完整。
在这里插入图片描述

3.3 卷积操作的数学原理

定义一个尺寸为 4×4 的输入矩阵 input：
$\left.input=\left[\begin{array}{cccc}x_1&x_2&x_3&x_4\\x_5&x_6&x_7&x_8\\x_9&x_{10}&x_{11}&x_{12}\\x_{13}&x_{14}&x_{15}&x_{16}\end{array}\right.\right]$
一个尺寸为3×3 的标准卷积核 kernel：
$kernel=\begin{bmatrix}w_{0,0}&w_{0,1}&w_{0,2}\\w_{1,0}&w_{1,1}&w_{1,2}\\w_{2,0}&w_{2,1}&w_{2,2}\end{bmatrix}$
令步长 $s t r i d es = 1$ ，填充 $p a dd in g = 0$ ，即 $i = 4, k = 3, s = 1, p = 0$ ，则按照 $公式 (1)$ 计算可得尺寸为 2×2的输出矩阵 $o u tp u t$ ：
$output=\begin{bmatrix}y_0&y_1\\y_2&y_3\end{bmatrix}$
这里，我们换一个表达方式，我们将输入矩阵 input 和输出矩阵 output 展开成列向量 X 和列向量 Y ，那么向量 X 和向量 Y 的尺寸就分别是 16×1 和 4×1，可以分别用如下公式表示：

把输入矩阵 input 展开成一个16×1列向量 $X$ ：
$\begin{array}{llllllllllll}X=[x_{1}&x_{2}&x_{3}&x_{4}&x_{5}&x_{6}&x_{7}&x_{8}&x_{9}&x_{10}&x_{11}&x_{12}&x_{13}&x_{14}&x_{15}&x_{16}]^T\end{array}$
把输出矩阵 $o u tp u t$ 展开成一个 4×1列向量 $Y$ ：
$Y=\begin{bmatrix}y_1&y_2&y_3&y_4\end{bmatrix}^T$
再用矩阵运算来描述标准卷积运算，这里使用矩阵 C 来表示标准卷积核矩阵：
$Y = CX$
经过推导，我们可以得到这个稀疏矩阵 C 的尺寸为 4×16：
$C=\begin{bmatrix}u_{0,0}&w_{0,1}&w_{0,2}&0&w_{1,0}&w_{1,1}&w_{1,2}&0&w_{2,0}&w_{2,1}&w_{2,3}&0&0&0&0&0\\0&w_{0,0}&w_{0,1}&w_{0,2}&0&w_{1,0}&w_{1,1}&w_{1,2}&0&w_{2,0}&w_{2,1}&w_{2,2}&0&0&0&0\\0&0&0&0&w_{0,0}&w_{0,1}&w_{0,2}&0&w_{1,0}&w_{1,1}&w_{1,2}&0&w_{2,0}&w_{2,1}&w_{2,2}&0\\0&0&0&0&0&w_{0,0}&w_{0,1}&w_{0,2}&0&w_{1,0}&w_{1,1}&w_{1,2}&0&w_{2,0}&w_{2,1}&w_{2,2}\end{bmatrix}$
上述矩阵运算如下图所示：
在这里插入图片描述

3.4 卷积计算公式

卷积计算的输入输出特征图尺寸的对应关系如下：
$o=\left\lfloor\frac{i+2p-k}{s}\right\rfloor+1 \quad \begin{array}{l} \\i=\textit{size of input}\\o=\textit{size of output}\\p=padding\\k=\textit{size of kernel}\\s=strides\end{array}\quad (1)$

其中， $\left\lfloor\cdot\right\rfloor$ 表示向下取整符号。

3.5 卷积参数量和计算量

卷积的三种模式:full, same, valid
卷积中参数量和计算量
卷积神经网络中的参数计算
理解分组卷积和深度可分离卷积如何降低参数量
网络解析（一）：LeNet-5详解
图像识别-AlexNet网络结构详解
抽丝剥茧，带你理解转置卷积（反卷积）
深度学习中不同类型卷积的综合介绍：2D卷积、3D卷积、转置卷积、扩张卷积、可分离卷积、扁平卷积、分组卷积、随机分组卷积、逐点分组卷积等pytorch代码实现和解析。

//TODO

参数量（神经元数量）的概念：参与计算的参数个数，占用内存空间。
计算量，运算量（连接数）：包括乘法和加法计算。

3.6 `1x1`卷积

一般来说，1x1的卷积对神经网络特征的学习作用不大，通常用来做shape的调整，即升维和降维。

3.7 `1x1`特征图

当输入特征图的width和heigth为1时，此时输出将由卷积核大小唯一决定，即卷积核若为nxn，则输出特征图大小也为nxn，后续计算可在此基础上继续套用卷积计算公式。

4. 池化层

4.1 引言

一个96x96的图像，如果用一个8x8大小的卷积核，每个特征的维度为(96-8+1)x(96-8+1)（假设padding使用VALID，步长strides为1）。定义400个特征（通道），最后的维度即为7921x400=3168400 大小的向量。最后再使用全连接进行分类的话，最后是三百万的卷积特征输入，由于维度太高十分容易出现过拟合。这时就需要用到池化。

4.2 池化层作用

池化又称作下采样，池化层通常在卷积层和激活层之后。池化层没有相应的参数，它往往存在于连续的卷积层之间。通过卷积和池化分别进行特征提取以及降维的目的。池化在图像识别中应用较多，但在一些网络模型的应用比如图像重建等并没有采用池化。

池化层是对不同位置的特征进行聚合统计。例如可以计算一个区域上某个特定特征的平均值（average_pooling），或者最大值（max_pooling）。最大值池化是最经常使用的池化方式，选取区域的最大值能够很好地保持原图的特征。在这一步操作过后不仅能够得到低得多的维度，还会增强泛化性能。

池化层是对卷积层提取到的特征再一次压缩。一方面，卷积输出中包含的大部分信息是冗余的，通过池化操作获得更主要的特征，防止出现过拟合现象；另一方面，通过池化操作减小输入的大小，减少输出中相似值的数量，从而减少参数的数量来简化网络计算的复杂性，提高网络模型的鲁棒性、容错性和运行效率。

4.3 池化层分类

最大池化(Max Pooling)。选择图像某一区域像素的最大值作为该区域池化操作后的数值。
平均池化(Average Pooling)。选择图像某一区域像素的平均值作为该区域池化操作后的数值。

4.4 池化计算公式

池化的计算与卷积计算类似，只是将stride步长设置为2，使得输出大小减半。
$o=\left\lfloor\frac{i+2p-k}{2}\right\rfloor+1 \quad \begin{array}{l} \\i=\textit{size of input}\\o=\textit{size of output}\\p=padding\\k=\textit{size of kernel}\\s=strides\end{array}\quad (2)$

其中， $\left\lfloor\cdot\right\rfloor$ 表示向下取整符号。

5. 全连接层

全连接层常常出现在整个卷积神经网络的末尾处，将所有的局部特征连接起来。如果说卷积层是用来提取局部特征，那么全连接层就是把所有的局部特征通过权值矩阵进行整合，并进行归一化操作，最后对各种分类情况都输出一个概率值。全连接层的输出是一个一维向量，一方面可以起到维度变换的作用，特别是可以将高维度转变为低维度，同时把有用的信息保留下来；另一方面可以起到“分类器”的作用，根据全连接得到的概率完成对特征的分类。

6. 常用CNN网络架构

常见的CNN网络架构可以被切成三个部分：

Stem: 将输入图像用少量的 convolution 扫过，并调整分辨率度。

Body: 网络的主要部分，又可分为多个stage，通常每个stage执行一次下采样（降低分辨率）的操作，其内部则为一个或多个building block (如residual bottleneck)的重复组合。

Head: 使用stem与body提取的feature，执行目标任务的预测。
在这里插入图片描述

除此之外，Building block也是一个很常被使用的术语，指的是那些被不断重复使用的小网络组合，比如说ResNet中的 residual block、residual bottleneck block，又或是MobileNet中的depthwise convolution block 与 reverted bottleneck block。

7. 关于CNN网络的深度/宽度/分辨率

在不大幅改动主架构的情况下，一般调整的参数有以下三种：

7.1 深度D(depth)

深度是指从输入到输出，堆叠的 building block 或 convolution layer 的数量。在深度方面，越深的网络可以捕捉越复杂的特征，并且带来更好的泛化 (generalization) 能力。然而，过深的网络即使使用 skip connection 与 batch normalization，仍然容易因梯度消失 (gradient vanishing) 导致不易训练。

7.2 宽度W (width)

宽度是指 building block 或 convolution layer 输出 feature map的宽度 (channels或filters数)。在宽度方面，一般来说越宽的网络可以捕捉到更细节 (fine-grained) 的信息，并且容易训练。然而，宽而浅的网络却是难以捕捉复杂的特征。

7.3 分辨率R(resolution)

分辨率是指 building block 或 convolution layer输出 feature map 张量的长与宽。在分辨率方面，高分辨率无庸置疑的可以得到更多细节信息，在大多的论文中基本上都是提升performance的好法宝。显而易见的缺点就是运算量，然后在localization问题需要调整、匹配的receptive field。