ABSTRACT

   交通流分析、预测和管理是新时代智慧城市建设的关键。借助深度神经网络和大交通数据，我们可以更好地理解复杂交通网络中隐藏的潜在模式。一条道路上的交通流动态不仅依赖于时间维度上的顺序模式，还依赖于空间维度上的其他道路。虽然目前已有预测未来交通流量的工作，但大多数工作在空间和时间依赖性建模方面存在一定的局限性。在本文中，我们提出了一种新的用于交通流预测的时空图神经网络，它可以全面地捕捉时空模式。特别是，该框架提供了一种可学习的位置注意机制，以有效地聚集来自相邻道路的信息。同时，它提供了一个顺序组件来建模交通流动态，可以利用局部和全局的时间依赖性。在各种真实交通数据集上的实验结果证明了该框架的有效性。

本文创新点：

1. 提出了一种新的具有位置注意机制的图神经网络层，以更好地聚合邻近道路的交通流信息;
2. 结合了RNN和Transformer，以捕获局部和全局的时间依赖性;
3. 提出了一个新的时空GNN框架STGNN，该框架专门用于建模具有复杂拓扑和时间依赖性的系列数据

 

问题描述

   给定交通网络g=(V, E)和历史交通信息y=(Y1,Y2,..,Yn),我们的目的是建立一个模型f，可以将一个长度为T的新序列X=(X1,…,XT)作为输入，预测未来T’个时间步的交通信息Xpred=(XT+1,…,XT+T’)。

  每一个交通流网络可以被定义为G = (V, E)，其中V = {v1, . . . ,vN } ,是包含N个交通传感器节点（一段路经常会有多个传感器节点），然后E则代表连接这些节点的边。adjacency matrix定义为A ∈ R N ×N，如果不联通的话就是A[i，j] = 0 。历史交通流信息就可以被表示为：Y = (Y1, . . . , Yτ ) 。交通流预测问题就可以定义如下

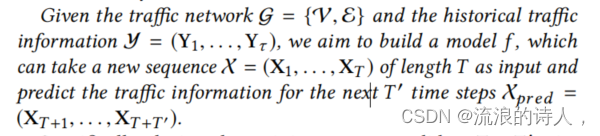
模型框架：

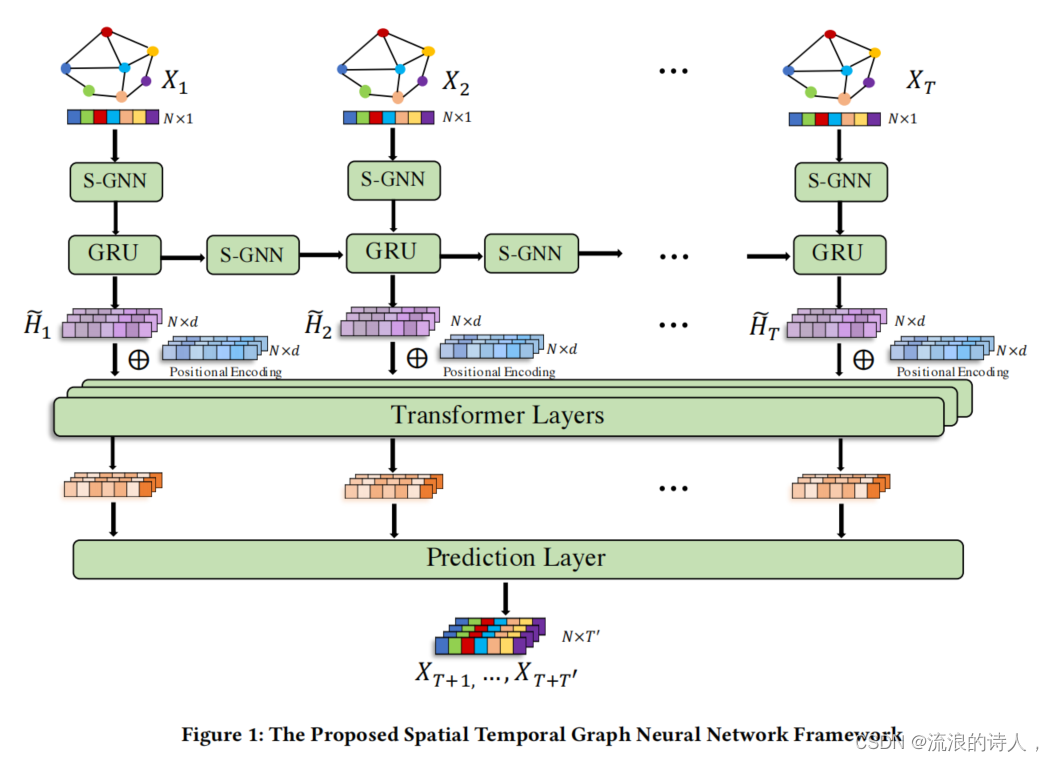
主要包含三块：

1. S-GNN层（空间）
   通过交通网络来捕捉道路之间的空间关系，注意，S-GNN层被用来建模节点之间的空间关系，它被应用于GRU单元的输入和隐藏表示的操作（用在俩地方）。
2. GRU层（时间-局部）
   按顺序捕获时间关系(或局部时间依赖)
3. transformer层（时间-全局）
   直接捕捉序列中的长期时间依赖(或全局时间依赖)，GRU层和transformer层分别用于捕获每个节点的时间依赖关系，从不同的角度罢了。

本文所提出的时空图神经网络框架如图所示。它主要由三个部分组成：1）空间图神经网络（S-GNN）层，旨在捕获通过交通网络的道路之间的空间关系；2）GRU层，该GRU层是用来按顺序捕获时间关系（或局部时间相关性）；3）Transformer层，其目的是直接捕获序列中的长期时间依赖性（或全局时间依性）。其中，S-GNN层用于建模节点之间的空间关系，并将其应用于GRU单元的输入和隐藏表示。需要注意的是GRU层和Transformer层都用于分别捕获每个节点的时间依赖性，但是分别是从不同角度捕获时间依赖性。

算法如下：

主要看一下S-GNN,作者的主要灵感来自于对GaAN的改进

1.S-GNN

交通网络G对道路之间的关系进行编码。交通网络中连通的道路更有可能具有相似的属性。具体到交通流预测问题中，如果两条道路相距较近，则道路上的交通状况更有可能相互影响。于是作者用了下边这个公式代表S-GNN操作。里边的 σ 是非线性操作，作者用了ReLU。 W就是要学的参数。

简化一下变成：

本文中使用了一种空间图卷积神经网络的方法去捕捉路网空间上的相关性。其中在图神经网络中引入了注意力机制以学习邻居节点对于中心节点的贡献度，但是稍微不同于图注意力神经网络GAT，在这里的注意力计算的所需参数更少。注意力计算的公式如下所示：

GaAN试图利用注意力机制对道路之间的复杂关系进行建模。然而，在计算注意力分数时，GaAN只利用了速度信息。理想情况下，我们可以使用上述因素来计算注意力得分。然而，这些因素并不总是可用的。此外，可能还有一些我们没有意识到的其他因素影响节点之间的关系。于是作者提出了一种位置表示来捕捉每个节点的这些因素、对于每一个节点 vi 我们试着学习一个潜在位置表示 pi  ,于是就能得到了任意俩路节点的相似性公式：

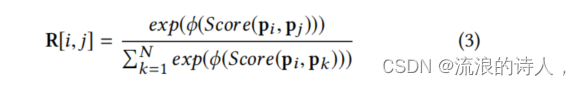
其中代表一种激活函数，pi和pj代表不同节点i和j的潜空间特征。Score( )是一种评分函数，在本文中没有像GAT中使用参数化的方法计算评分函数，而是直接用pi和pj的点积区去计算。在这里仍然采用了与GAT中相同的mask机制用计算得到的权重值替换原邻接矩阵中的非零元素。

作者还简化了W,采用掩膜办法降低计算量：

然后就用GCN操作，进行迭代

说白了这块就是改了一下GaNN里边相似性计算的部分，还增加了一点减少计算的小技巧。

所以整个文章主要就是采用了多种操作，把时空结合来做，这里边GRU和Transformer的结合可以借鉴。

2)GRU层

GRU的作用是捕捉每个空间节点在时间维度上的短时依赖，在这里每个GRU单元的输入Xt和隐藏层输出Ht-1都要经过S-GNN的计算：

本文中总的GRU公式与普通的GRU公式区别不大，主要需要注意的地方是输入和隐藏层都要经由S-GNN以捕捉空间的关系。

(3)Transformer层

Transformer是一种适合学习长序列的神经网络模型，弥补了RNN系列模型在误差积累，梯度爆炸，长时记忆等方面的短板，其作用是捕捉每个空间节点在时间维度上的长时依赖。这里的Transformer层与一般的Transformer基本结构别无二致，分别由位置编码机制，多头注意力层和前馈输出层组成。Transformer层的输入为GRU层中每个循环单元的输出。

Transformer中最核心的还是自注意力机制。本文中的单个自注意力计算与原始的自注意力计算公式一致，分别为查询向量Q、键向量K和值向量V组成：
 

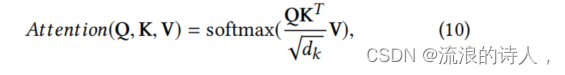
为了提升训练的稳定性，可采用多头形式的自注意力：

本文中Transformer总体结构如下图所示：

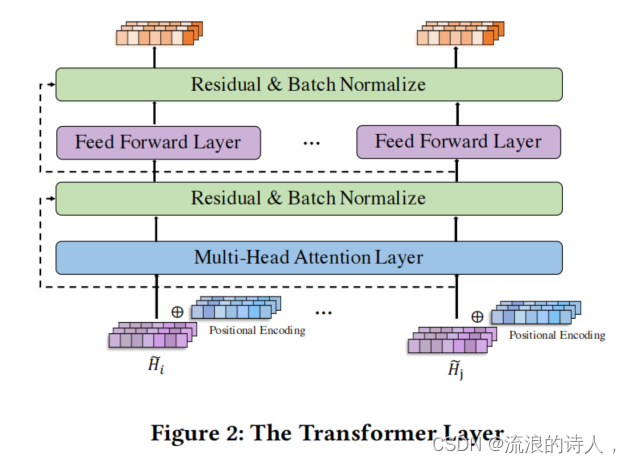
最后在Transformer层的末端接上一个Prediction Layer, 一个普通的前馈神经网络，直接输出未来T’个时间步的交通信息。论文中用MAE作为整体模型训练的损失函数。

实验结果

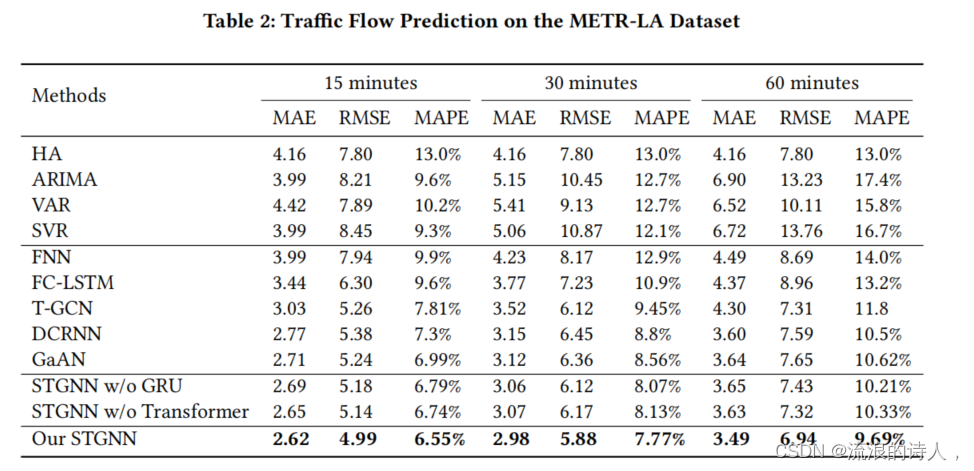
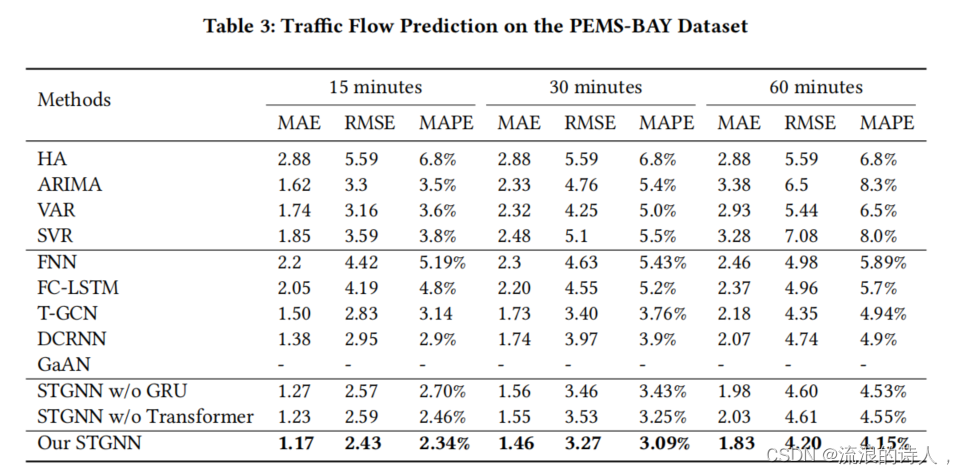
  论文中使用了两个数据集，分别是METR-LA和PEMS-BAY两个道路速度传感器网络数据。分别对于时间片切分为15分钟，30分钟和60分钟的情况下做了实验，并设计移除GRU的变体STGCN w/o GRU和移除Transformer的变体STGCN w/o Transformer, 证明了同时捕捉短时时间依赖和长时时间依赖的有效性。总体试验结果表明该模型优于其他方法。
 

 

 

创新点

本文的最大亮点是引入了Transformer模型应用于交通预测领域并首次提出了在交通预测中结合时间维度的局部特征和全局特征的模型。但是运用RNN于较长序列仍然会带来误差积累，并且RNN模型的运算效率并不高，可以考虑运用一维卷积模型对于短时依赖进行捕捉。

Attention