在循环神经网络中,当时间步数较大或者时间步较小时,循环神经网络的梯度较容易出现衰减或爆炸。上一篇文章中介绍的裁剪梯度可以应对梯度爆炸,但无法解决梯度衰减的问题。因此,循环神经网络在实际中较难捕捉时间序列中时间步距离较大的依赖关系。
为了更好地捕捉时间序列中时间步距离较大的依赖关系,从而提出了门控循环神经网络(gated recurrent neural network)。它可以通过学习的门来控制信息的流动。其中,门控循环单元(gated recurrent unit,GRU)是一种常用的门控循环神经网络 。
目录
- 1. 门控循环单元设计
- 1.1 重置门和更新门
- 1.2 候选隐藏状态
- 1.3 隐藏状态
- 2 读取数据集
- 3 从零实现门控循环单元并进行歌词训练与预测
- 3.1 初始化模型参数
- 3.2 定义模型
- 3.3 训练模型并创作歌词
- 4 基于Pytorch的nn.GRU模块实现GRU并进行歌词训练与预测
- 总结
1. 门控循环单元设计
门控循环单元的设计在原始RNN的基础上引入了重置门(reset gate)和更新门(update gate)的概念,从而修改了循环神经网络中隐藏状态的计算方式。
1.1 重置门和更新门
如下图所示,门控循环单元中的重置门和更新门的输入均为当前时间步输入 X t \boldsymbol{X}_t Xt与上一时间步隐藏状态 H t − 1 \boldsymbol{H}_{t-1} Ht−1,输出由激活函数为sigmoid函数的全连接层计算得到。
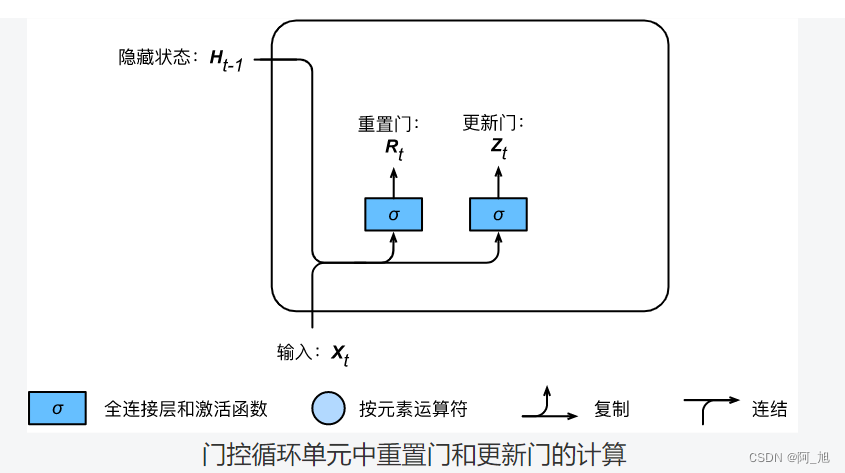
假设隐藏单元个数为 h h h,给定时间步 t t t的小批量输入 X t ∈ R n × d \boldsymbol{X}_t \in \mathbb{R}^{n \times d} Xt∈Rn×d(样本数为 n n n,输入个数为 d d d)和上一时间步隐藏状态 H t − 1 ∈ R n × h \boldsymbol{H}_{t-1} \in \mathbb{R}^{n \times h} Ht−1∈Rn×h。重置门 R t ∈ R n × h \boldsymbol{R}_t \in \mathbb{R}^{n \times h} Rt∈Rn×h和更新门 Z t ∈ R n × h \boldsymbol{Z}_t \in \mathbb{R}^{n \times h} Zt∈Rn×h的计算如下:
R t = σ ( X t W x r + H t − 1 W h r + b r ) , Z t = σ ( X t W x z + H t − 1 W h z + b z ) , \begin{aligned} \boldsymbol{R}_t = \sigma(\boldsymbol{X}_t \boldsymbol{W}_{xr} + \boldsymbol{H}_{t-1} \boldsymbol{W}_{hr} + \boldsymbol{b}_r),\\ \boldsymbol{Z}_t = \sigma(\boldsymbol{X}_t \boldsymbol{W}_{xz} + \boldsymbol{H}_{t-1} \boldsymbol{W}_{hz} + \boldsymbol{b}_z), \end{aligned} Rt=σ(XtWxr+Ht−1Whr+br),Zt=σ(XtWxz+Ht−1Whz+bz),
其中 W x r , W x z ∈ R d × h \boldsymbol{W}_{xr}, \boldsymbol{W}_{xz} \in \mathbb{R}^{d \times h} Wxr,Wxz∈Rd×h和 W h r , W h z ∈ R h × h \boldsymbol{W}_{hr}, \boldsymbol{W}_{hz} \in \mathbb{R}^{h \times h} Whr,Whz∈Rh×h是权重参数, b r , b z ∈ R 1 × h \boldsymbol{b}_r, \boldsymbol{b}_z \in \mathbb{R}^{1 \times h} br,bz∈R1×h是偏差参数。sigmoid函数可以将元素的值变换到0和1之间。因此,重置门 R t \boldsymbol{R}_t Rt和更新门 Z t \boldsymbol{Z}_t Zt中每个元素的值域都是 [ 0 , 1 ] [0, 1] [0,1]。
1.2 候选隐藏状态
接下来,门控循环单元将计算候选隐藏状态来辅助稍后的隐藏状态计算。如下图所示,我们将当前时间步重置门的输出与上一时间步隐藏状态做按元素乘法(符号为
⊙
\odot
⊙)。如果重置门中元素值接近0,那么意味着重置对应隐藏状态元素为0,即丢弃上一时间步的隐藏状态。如果元素值接近1,那么表示保留上一时间步的隐藏状态。然后,将按元素乘法的结果与当前时间步的输入连结,再通过含激活函数tanh的全连接层计算出候选隐藏状态,其所有元素的值域为
[
−
1
,
1
]
[-1, 1]
[−1,1]。

具体来说,时间步 t t t的候选隐藏状态 H ~ t ∈ R n × h \tilde{\boldsymbol{H}}_t \in \mathbb{R}^{n \times h} H~t∈Rn×h的计算为
H ~ t = tanh ( X t W x h + ( R t ⊙ H t − 1 ) W h h + b h ) , \tilde{\boldsymbol{H}}_t = \text{tanh}(\boldsymbol{X}_t \boldsymbol{W}_{xh} + \left(\boldsymbol{R}_t \odot \boldsymbol{H}_{t-1}\right) \boldsymbol{W}_{hh} + \boldsymbol{b}_h), H~t=tanh(XtWxh+(Rt⊙Ht−1)Whh+bh),
其中 W x h ∈ R d × h \boldsymbol{W}_{xh} \in \mathbb{R}^{d \times h} Wxh∈Rd×h和 W h h ∈ R h × h \boldsymbol{W}_{hh} \in \mathbb{R}^{h \times h} Whh∈Rh×h是权重参数, b h ∈ R 1 × h \boldsymbol{b}_h \in \mathbb{R}^{1 \times h} bh∈R1×h是偏差参数。从上面这个公式可以看出,重置门控制了上一时间步的隐藏状态如何流入当前时间步的候选隐藏状态。而上一时间步的隐藏状态可能包含了时间序列截至上一时间步的全部历史信息。因此,重置门可以用来丢弃与预测无关的历史信息。
1.3 隐藏状态
最后,时间步 t t t的隐藏状态 H t ∈ R n × h \boldsymbol{H}_t \in \mathbb{R}^{n \times h} Ht∈Rn×h的计算使用当前时间步的更新门 Z t \boldsymbol{Z}_t Zt来对上一时间步的隐藏状态 H t − 1 \boldsymbol{H}_{t-1} Ht−1和当前时间步的候选隐藏状态 H ~ t \tilde{\boldsymbol{H}}_t H~t做组合:
H t = Z t ⊙ H t − 1 + ( 1 − Z t ) ⊙ H ~ t . \boldsymbol{H}_t = \boldsymbol{Z}_t \odot \boldsymbol{H}_{t-1} + (1 - \boldsymbol{Z}_t) \odot \tilde{\boldsymbol{H}}_t. Ht=Zt⊙Ht−1+(1−Zt)⊙H~t.

更新门可以控制隐藏状态应该如何被包含当前时间步信息的候选隐藏状态所更新,如上图所示。假设更新门在时间步 t ′ t' t′到 t t t( t ′ < t t' < t t′<t)之间一直近似1。那么,在时间步 t ′ t' t′到 t t t之间的输入信息几乎没有流入时间步 t t t的隐藏状态 H t \boldsymbol{H}_t Ht。实际上,这可以看作是较早时刻的隐藏状态 H t ′ − 1 \boldsymbol{H}_{t'-1} Ht′−1一直通过时间保存并传递至当前时间步 t t t。这个设计可以应对循环神经网络中的梯度衰减问题,并更好地捕捉时间序列中时间步距离较大的依赖关系。
总结:
- 重置门有助于捕捉时间序列里短期的依赖关系;
- 更新门有助于捕捉时间序列里长期的依赖关系。
2 读取数据集
为了实现并展示门控循环单元,下面依然使用上一篇文章中的周杰伦歌词专辑数据集来训练模型作词。
数据集获取参见上一篇文章《【从零开始学习深度学习】34. Pytorch-RNN项目实战:RNN创作歌词案例–使用周杰伦专辑歌词训练模型并创作歌曲【含数据集与源码】》。
import numpy as np
import torch
from torch import nn, optim
import torch.nn.functional as F
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
(corpus_indices, char_to_idx, idx_to_char, vocab_size) = d2l.load_data_jay_lyrics()
3 从零实现门控循环单元并进行歌词训练与预测
3.1 初始化模型参数
对模型参数进行初始化,超参数num_hiddens定义了隐藏单元的个数。
num_inputs, num_hiddens, num_outputs = vocab_size, 256, vocab_size
print('will use', device)
def get_params():
def _one(shape):
ts = torch.tensor(np.random.normal(0, 0.01, size=shape), device=device, dtype=torch.float32)
return torch.nn.Parameter(ts, requires_grad=True)
def _three():
return (_one((num_inputs, num_hiddens)),
_one((num_hiddens, num_hiddens)),
torch.nn.Parameter(torch.zeros(num_hiddens, device=device, dtype=torch.float32), requires_grad=True))
W_xz, W_hz, b_z = _three() # 更新门参数
W_xr, W_hr, b_r = _three() # 重置门参数
W_xh, W_hh, b_h = _three() # 候选隐藏状态参数
# 输出层参数
W_hq = _one((num_hiddens, num_outputs))
b_q = torch.nn.Parameter(torch.zeros(num_outputs, device=device, dtype=torch.float32), requires_grad=True)
return nn.ParameterList([W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q])
3.2 定义模型
定义隐藏状态初始化函数init_gru_state,它返回由一个形状为(批量大小, 隐藏单元个数)的值为0的Tensor组成的元组。
def init_gru_state(batch_size, num_hiddens, device):
return (torch.zeros((batch_size, num_hiddens), device=device), )
下面根据门控循环单元的计算表达式定义模型。
def gru(inputs, state, params):
W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q = params
H, = state
outputs = []
for X in inputs:
Z = torch.sigmoid(torch.matmul(X, W_xz) + torch.matmul(H, W_hz) + b_z)
R = torch.sigmoid(torch.matmul(X, W_xr) + torch.matmul(H, W_hr) + b_r)
H_tilda = torch.tanh(torch.matmul(X, W_xh) + torch.matmul(R * H, W_hh) + b_h)
H = Z * H + (1 - Z) * H_tilda
Y = torch.matmul(H, W_hq) + b_q
outputs.append(Y)
return outputs, (H,)
3.3 训练模型并创作歌词
我们在训练模型时只使用相邻采样。设置好超参数后,我们将训练模型并根据前缀“分开”和“不分开”分别创作长度为50个字符的一段歌词。
num_epochs, num_steps, batch_size, lr, clipping_theta = 160, 35, 32, 1e2, 1e-2
pred_period, pred_len, prefixes = 40, 50, ['分开', '不分开']
我们每过40个迭代周期便根据当前训练的模型创作一段歌词。
d2l.train_and_predict_rnn(gru, get_params, init_gru_state, num_hiddens,
vocab_size, device, corpus_indices, idx_to_char,
char_to_idx, False, num_epochs, num_steps, lr,
clipping_theta, batch_size, pred_period, pred_len,
prefixes)
输出:
epoch 40, perplexity 152.550790, time 2.29 sec
- 分开 我不不 你不我 你不我 你不我 你不我 你不我 你不我 你不我 你不我 你不我 你不我 你不我 你
- 不分开 一哼我 我不不 你不了我 你不我 你不我 你不我 你不我 你不我 你不我 你不我 你不我 你不我
epoch 80, perplexity 32.991306, time 2.28 sec
- 分开 我想要这样的微笑在人人卷戏 爱不再再我 你的美美 你在完人 你在在人的溪边默默默默默著著我 娘子
- 不分开 我不能再想 我不要再想 我不能再想 我不能再想 我不能再想 我不能再想 我不能再想 我不能再想 我
epoch 120, perplexity 6.238240, time 2.39 sec
- 分开 我想就这样牵着你的手不放开 爱可不可以简简单单没有伤害 你 靠着我的肩膀 你 在我胸口睡著 一定个
- 不分开 不知再觉 你是一个人演慢 一直风 三步三步步步四望 连成线背著背默默许下心愿 看远方的星如下听的见
epoch 160, perplexity 1.926641, time 2.64 sec
- 分开 我不要再宣牵我对你 感感 让给我抬起你有 从杰去真医 你在过人 何都没有 说我该轻的证 从情着头
- 不分开 不知再觉 你是心蒙 迷迷了中留的寻找 停堡里一只点芜 长满杂草的泥剩 不会骑扫二的胖女还 用拉丁文
4 基于Pytorch的nn.GRU模块实现GRU并进行歌词训练与预测
在PyTorch中我们直接调用nn模块中的GRU类即可。
lr = 1e-2 # 注意调整学习率
gru_layer = nn.GRU(input_size=vocab_size, hidden_size=num_hiddens)
model = d2l.RNNModel(gru_layer, vocab_size).to(device)
d2l.train_and_predict_rnn_pytorch(model, num_hiddens, vocab_size, device,
corpus_indices, idx_to_char, char_to_idx,
num_epochs, num_steps, lr, clipping_theta,
batch_size, pred_period, pred_len, prefixes)
输出:
epoch 40, perplexity 1.017262, time 0.87 sec
- 分开始乡相信命运 感谢地心引力 让我碰到你 漂亮的让我面红的可爱女人 温柔的让我心疼的可爱女人 透明的让
- 不分开始打呼 管家是一只会说法语举止优雅的猪 吸血前会念约翰福音做为弥补 拥有一双蓝色眼睛的凯萨琳公主 专
epoch 80, perplexity 1.015187, time 1.22 sec
- 分开始乡相信命运 感谢地心引力 让我碰到你 漂亮的让我面红的可爱女人 温柔的让我心疼的可爱女人 透明的让
- 不分开 它一定实现 娘子 娘子却依旧每日 折一枝杨柳 你在那里 在小村外的溪边河口默默等著我 娘子依旧每日
epoch 120, perplexity 1.013440, time 0.85 sec
- 分开始乡相信命运 感谢地心引力 让我碰到你 漂亮的让我面红的可爱女人 温柔的让我心疼的可爱女人 透明的让
- 不分开 陷入了危险边缘Baby 我的世界已狂风暴雨 Wu 爱情来的太快就像龙卷风 离不开暴风圈来不及逃
epoch 160, perplexity 1.910635, time 0.82 sec
- 分开的话你甘会听 有教堂有城堡 每天忙碌地的寻找 到底什么我有多烦恼 没有你烦我有多烦恼 没有多烦恼
- 不分开 别发抖 快给我抬起头 有话去对医药箱说 别怪我 别发抖 快给我抬起头 有话去对医药箱说 别怪我 别
总结
- 门控循环神经网络可以更好地捕捉时间序列中时间步距离较大的依赖关系。
- 门控循环单元引入了门的概念,从而修改了循环神经网络中隐藏状态的计算方式。它包括重置门、更新门、候选隐藏状态和隐藏状态。
- 重置门有助于捕捉时间序列里短期的依赖关系。
- 更新门有助于捕捉时间序列里长期的依赖关系。
如果文章内容对你有帮助,感谢点赞+关注!