曲线全局逼近

本文是基于 这篇文章 翻译而来的，仅学习。

在插值中，插值曲线以给定的顺序通过所有给定的数据点。正如在全局插值页面中所讨论的，插值曲线可能会在所有数据点上摆动，而不是紧紧跟随数据多边形。为了克服这个问题，引入了逼近技术，放宽了曲线必须包含所有数据点的严格要求。在全局近似中，除了第一个和最后一个数据点外，曲线不必包含每个点。

为了测量曲线“近似”给定数据多边形的程度，使用了误差距离的概念。误差距离是数据点与其曲线上的“对应”点之间的距离。因此，如果这些误差距离的总和最小化，曲线应该紧密地跟随数据多边形的形状。插值曲线当然是这样一种解决方案，因为每个数据点的误差距离都是零。然而，要讨论的公式不太可能产生插值曲线。用这种方法得到的曲线称为近似曲线。

假设我们有n+1个数据点D₀, D₁，…， D_n，并希望找到一条b样条曲线，它遵循数据多边形的形状，而不实际包含数据点。为此，我们需要另外两个输入：控制点的数量(即h+1)和度数( p )，其中必须保持n > h >= p >= 1。因此，近似比插值更灵活，因为我们不仅选择了度数，还选择了控制点的数量。以下是对我们问题的总结：
least square：最小二乘

有了h和p，我们可以确定一组参数和节点向量。设参数为t₀, t₁，…， t_n。注意，参数的数量等于数据点的数量。假设p次b样条曲线的近似是

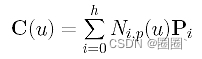
其中P₀, P₁，…， P_h为 h+1 个未知控制点。由于我们希望曲线通过第一个和最后一个数据点，我们有D₀ = C(0) = P₀和D_n = C(1) = p_h。因此，只有 h - 1 个未知控制点P₁, P₂，…, P_h-1。考虑到这一点，曲线方程如下所示:

最小二乘的意义

我们如何测量误差距离？由于参数t_k对应数据点D_k，因此D_k与曲线上t_k对应点的距离为|D_k - C(t_k)|。由于该距离由一个平方根组成，不容易处理，因此我们选择使用平方距离|D_k - C(t_k)|²。因此，所有误差距离的平方和为

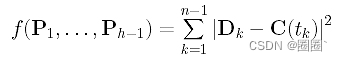
当然，我们的目标是找到那些控制点P₁，…， P_h-1，使得函数f()最小化。因此，近似是在最小二乘意义下进行的。

寻找解决方案

这部分有点乱，需要一些线性代数的知识。首先，让我们把D_k - C(t_k)改写成另一种形式:

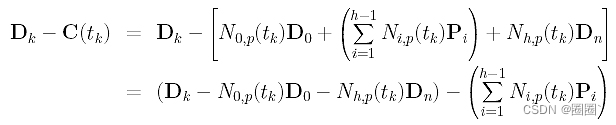
上面给出了D₀, D_k和D_n，通过计算N_0,p(u)和N_h,p(u)可以得到N_0,p(t_k)和N_h,p(t_k)。点击这里学习如何计算这些系数。为了方便起见，我们定义一个新的向量Q_k为:

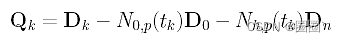
那么平方和函数f()可以写成:

接下来，我们将找出误差距离的平方。回想恒等式x·x = |x|²。这意味着向量x与自身的内积给出了x长度的平方。因此，误差平方项可以重写为

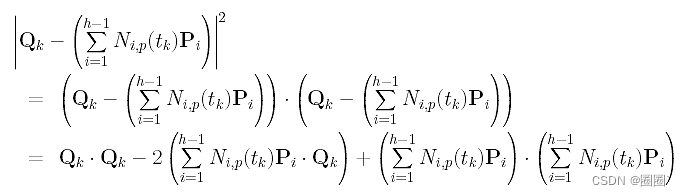
然后，f()函数为：

我们如何最小化这个函数?函数f()实际上是一个椭圆抛物面，变量P₁，…, P_h-1。因此，我们对f()对每个P_g进行微分，并找到这些偏导数的公共零。这些0是函数f()达到其最小值时的值。

在计算对P_g的导数时，请注意所有Q_k和N_i,p(t_k)都是常数(即不涉及P_k)，它们对任何P_g的偏导数必须为零。因此，我们有

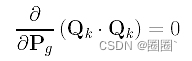
考虑求和中的第二项，它是N_i,p(t_k)P_i · Q_k的和。各子项的导数计算如下:

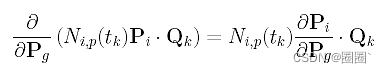
只有当i = g时，P_i对P_g的偏导数是非零的，因此，第二项的偏导数为:

第三项的导数更复杂；但这仍然很简单。下面使用乘法规则(f·g)’ = f ‘·g + f·g’。

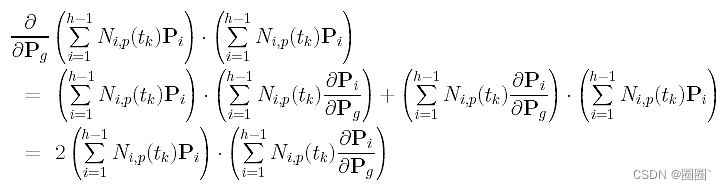
如果i不等于g，则P_i对P_g的偏导数为零，因此求和中的第三项对P_g的偏导数为:

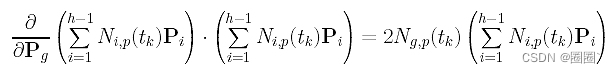
结合这些结果，f()对P_g的偏导数为

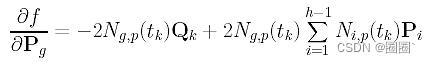
将其设置为0，我们得到以下内容:

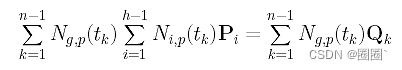
因为我们有h-1变量，g从1到h-1，有h-1这样的方程。注意，这些方程在未知数P_i中是线性的。在继续之前，我们先定义三个矩阵:

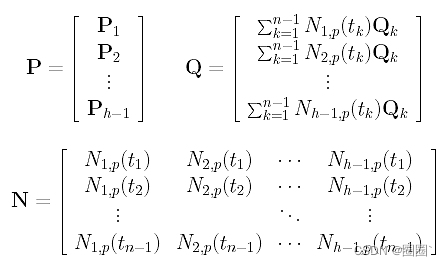
这里，P的第k行是向量P_k, Q的第k行是上面第k个方程的右边，N的第k行包含了在t_k 计算 N_1,P(u)， N_2,P(u)，…， N_h-1,p(u)的值。因此，如果输入数据点是s维向量，P、N和Q分别是(h-1)×s、(N -1)×(h-1)和(h-1)×s矩阵。

现在我们重写第g个线性方程

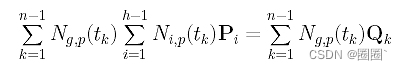
转换成另一种形式，以便容易读出P_i的系数：

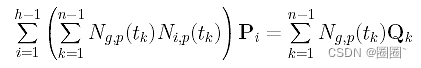
最后，P_i的系数是

如果你观察矩阵N，你会看到N_g,p(t₁)， N_g,p(t₂)，…， N_g,p(t_n-1)为N的第g列，N_i,p(t₁)， N_i,p(t₂)，…， N_i,p(t_n-1)是N的第i列。注意，N的第g列是N的转置矩阵 N^T的第g行，P_i的系数是N^T的第g行和N的第i列的“内积”。根据这种观察，线性方程组可以重写为

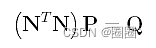
由于N和Q是已知的，求解P的线性方程组可以得到所需的控制点。当然，我们已经找到了解决方案。

算法

虽然上一节的开发过程冗长而乏味，但最终结果却出奇地简单：解一个线性方程组，就像我们在全局插值中遇到的那样。因此，全局近似的算法也非常简单。

• 输入：n+1个数据点D₀, D₁，…， D_n，度p，所需控制点数量h+1;

• 输出：p次b样条曲线，由h+1个控制点定义，逼近给定的数据点;

• 算法：
  Obtain a set of parameters t₀, …, t_n and a knot vector U;
  Let P₀ = D₀ and P_h = D_n;
  for k := 1 to n-1 do
       Compute Q_k with the following formula:
  
  for i := 1 to h-1 do
       Compute the following and save it to the i-th row of matrix Q;
  

  /* matrix Q is available /
  for k := 1 to n-1 do
       for i := 1 to h-1 do
           Compute N_i,p(t_k) and save to row k and column i of N;
  / matrix N is available */
  Compute M = N^T·N;
  Solving for P from M·P = Q;
  Row i of P is control point P_i;
  Control points P₀, …, P_h, knot vector U and degree p determines an approximation B-spline curve;

度和控制点数量的影响

很明显，数据点对近似曲线的形状有影响。p度和控制点的数量对曲线形状的影响是什么?下图显示了10个数据点(n=9)在不同的度数和控制点数量下的近似曲线。每一行给出次数相同但控制点个数不同的近似曲线，每一列给出次数相同但控制点个数不同的近似曲线。注意，所有曲线都使用向心方法来计算其参数。

可以理解的是，低阶曲线通常不能很好地逼近数据多边形，因为它们不是很灵活。因此，在每一列上，阶数越高，结果越好(即越接近数据多边形)。基于同样的原因，控制顶点越多，逼近曲线的灵活性越高。因此，在每一行上，随着控制点数量的增加，曲线变得更接近数据多边形。

我们应该使用高阶曲线和许多控制点吗?答案是否定的，因为全局逼近可能比全局插值使用更少的控制点。如果控制点的数量等于数据点的数量，全局逼近就变成了全局插值，我们就可以使用全局插值！至于次数，我们当然希望是最小的次数，只要生成的曲线能符合数据多边形的形状。

为什么这个方法是全局的?

这种近似方法是全局的，因为改变数据点的位置会导致整个曲线发生变化。下图中的黄色点是给定的数据点，将被3次b样条曲线和5个控制点(即n = 7, p=3和h = 4)近似。参数是用向心方法计算的。假设数据点4被移动到一个由浅蓝色点表示的新位置。新的近似b样条是蓝色的。如你所见，除了第一个和最后一个数据点被算法固定外，原始曲线和新曲线的形状非常不同。因此，由于修改数据点而产生的变化是全局的！

补充：距离度量常见的有几何距离和代数距离。几何距离表示某点到曲线最近点的距离。平面内某点（x0,y0）到方程 f(x,y)=0 所代表曲线的代数距离就是 f(x0,y0)。