题目一:DS静态查找 -- 顺序查找
题目描述:
给出一个队列和要查找的数值,找出数值在队列中的位置,队列位置从1开始
要求使用带哨兵的顺序查找算法
输入要求:
第一行输入n,表示队列有n个数据
第二行输入n个数据,都是正整数,用空格隔开
第三行输入t,表示有t个要查找的数值
第四行起,输入t个数值,输入t行
输出要求:
每行输出一个要查找的数值在队列的位置,如果查找不成功,输出字符串error
输入样例:
8
33 66 22 88 11 27 44 55
3
22
11
99
输出样例:
3
5
error代码示例:
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int sequenceSearch(int arr[], int key, int n) {
int i = n;
arr[0] = key;//设置哨兵
while (arr[i] != key) i--;
return i;
}
int main() {
int n;
int array[10010];
cin >> n;
for (int i = 1; i <= n; i++) cin >> array[i];
int t;
cin >> t;
while (t--) {
int k;
cin >> k;
int index = sequenceSearch(array, k, n);
if (index) cout << index << endl;
else cout << "error" << endl;
}
}题目二:DS静态查找 -- 折半查找
题目描述:
给出一个队列和要查找的数值,找出数值在队列中的位置,队列位置从1开始
要求使用折半查找算法
输入要求:
第一行输入n,表示队列有n个数据
第二行输入n个数据,都是正整数,用空格隔开
第三行输入t,表示有t个要查找的数值
第四行起,输入t个数值,输入t行
输出要求:
每行输出一个要查找的数值在队列的位置,如果查找不成功,输出字符串error
输入样例:
8
11 22 33 44 55 66 77 88
3
22
88
99
输出样例:
2
8
error代码示例:
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int binarySearch(int arr[], int l, int r, int key) {
while (l < r) {
int mid = l + r >> 1;
if (arr[mid] >= key) r = mid;
else l = mid + 1;
}
return l;
}
int main() {
int n;
int array[10010];
cin >> n;
for (int i = 1; i <= n; i++) cin >> array[i];
int t;
cin >> t;
while (t--) {
int num;
cin >> num;
int index = binarySearch(array, 1, n, num);
if (array[index] != num) cout << "error" << endl;
else cout << index << endl;
}
}题目三:DS静态查找 -- 顺序索引查找
题目描述:
给出一个队列和要查找的数值,找出数值在队列中的位置,队列位置从1开始
要求使用顺序索引查找算法,其中索引表查找和块内查找都采用不带哨兵、从头开始的顺序查找方法。
输入要求:
第一行输入n,表示主表有n个数据
第二行输入n个数据,都是正整数,用空格隔开
第三行输入k,表示主表划分为k个块,k也是索引表的长度
第四行输入k个数据,表示索引表中每个块的最大值
第五行输入t,表示有t个要查找的数值
第六行起,输入t个数值,输入t行
输出要求:
每行输出一个要查找的数值在队列的位置和查找次数,数据之间用短划线隔开,如果查找不成功,输出字符串error
输入样例:
18
22 12 13 8 9 20 33 42 44 38 24 48 60 58 74 57 86 53
3
22 48 86
6
13
5
48
40
53
90
输出样例:
3-4
error
12-8
error
18-9
error代码示例:
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int main() {
int n;
int array[1010];
cin >> n;
for (int i = 1; i <= n; i++) cin >> array[i];
int x;
cin >> x;
int index[100], maxnum[100];
for (int i = 1; i <= x; i++) cin >> maxnum[i];
int pos = 2, maxindex = 1;
index[1] = 1;
for (int i = 2; i <= x; i++) {
for (int j = 1; j < n; j++) {
if (array[j] > maxnum[maxindex]) {
index[pos] = j;
maxindex++;
pos++;
}
}
}
int t;
cin >> t;
while (t--) {
int num;
cin >> num;
int cnt = 0;
int startpos = 0;
for (int i = 1; i <= x; i++) {
cnt++;
if (num <= maxnum[i]) {
startpos = index[i];
break;
}
}
if (!startpos) {
cout << "error" << endl;
continue;
}
for (int i = startpos; i <= n; i++) {
cnt++;
if (num == array[i]) {
cout << i << "-" << cnt << endl;
break;
}
else if (i == n) {
cout << "error" << endl;
}
}
}
}题目四:DS静态查找 -- 折半查找求平方根
题目描述:
假定输入y是整数,我们用折半查找来找这个平方根。在从0到y之间必定有一个取值是y的平方根,如果我们查找的数x比y的平方根小,则x2<y,如果我们查找的数x比y的平方根大,则x2>y,我们可以据此缩小查找范围,当我们查找的数足够准确时(比如满足|x2-y|<0.00001),就可以认为找到了y的平方根。
比如求5的平方根x,则x一定满足0<=x<=5,取x为(5+0)/2=2.5,因为2.5的平方为6.25>5,所以x一定小于2.5,也即x满足0<=x<=2.5,取x为1.25,以此类推
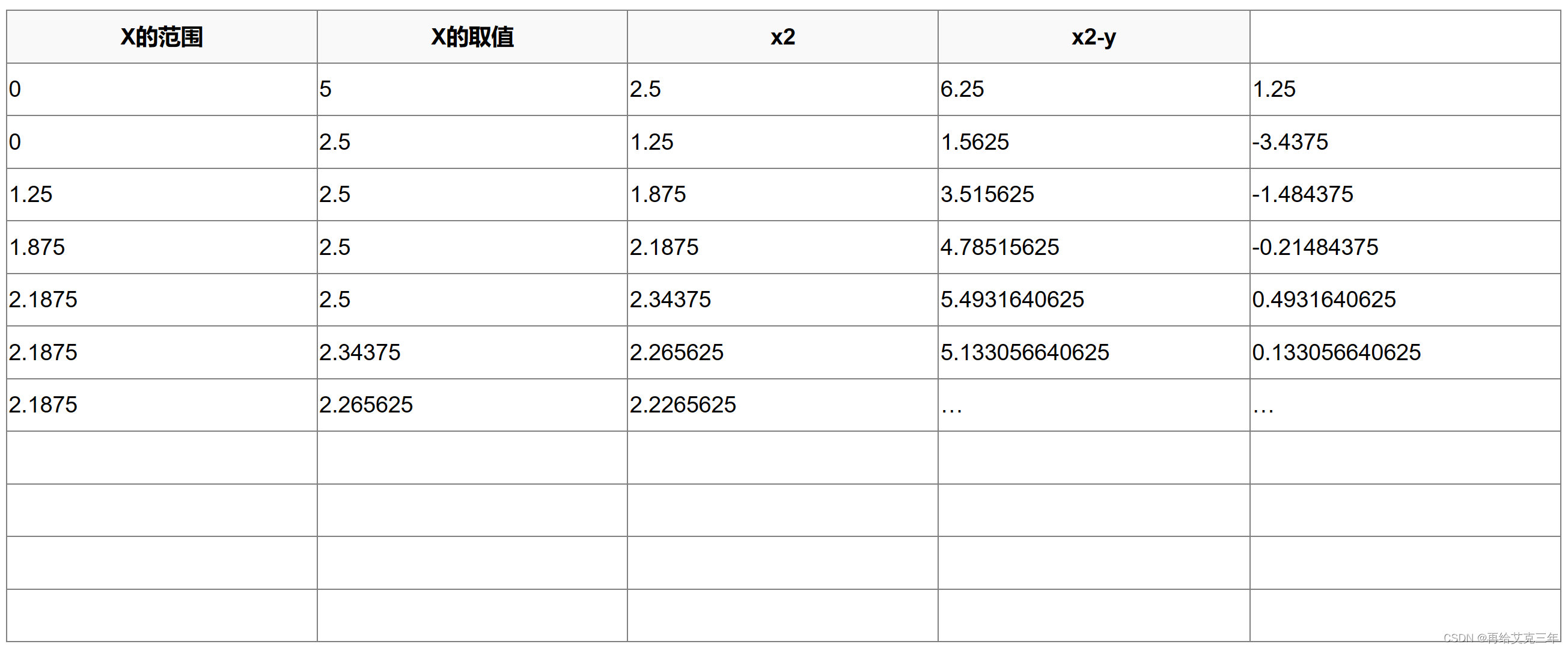
最后求得5的平方根为2.236
输入要求:
第1行输入一个整数n(<100),表示有n个数
从第2行起到第n+1行输入n个整数
输出要求:
输出n个数的平方根,精确到小数点后三位。
输入样例:
2
13
5
输出样例:
3.606
2.236代码示例:
#include <iostream>
#include <cmath>
#include <algorithm>
#include <iomanip>
using namespace std;
const double eps = 1e-8; // eps 表示精度,取决于题目对精度的要求
int main(){
int t;
cin >> t;
while (t--) {
double n;
cin >> n;
double l, r;
if (n >= 1) l = 1, r = n;
else if (n > 0) l = 0, r = 1;
else if (n <= -1) l = n, r = -1;
else l = -1, r = 0;
while (r - l > eps)
{
double mid = (l + r) / 2;
if (pow(mid, 2) >= n) r = mid;
else l = mid;
}
cout << fixed << setprecision(3) << l << endl;
}
}题目五:DS静态查找 -- 两个有序序列的中位数
题目描述:
已知有两个等长的非降序序列S1, S2, 设计函数求S1与S2并集的中位数。有序序列A0,A1,⋯,AN−1的中位数指A(N−1)/2的值,即第⌊(N+1)/2⌋个数(A0为第1个数)。
只需考虑中位数唯一的情况
4输入要求:
输入分三行。第一行给出序列的公共长度N(0<N≤100000),随后每行输入一个序列的信息,即N个非降序排列的整数。数字用空格间隔。
输出要求:
在一行中输出两个输入序列的并集序列的中位数。
输入样例:
5
1 3 5 7 9
2 3 4 5 6输出样例:
4代码示例:
#include <iostream>
#include <cmath>
#include <algorithm>
#include <iomanip>
using namespace std;
void quick_sort(int q[], int l, int r){
if (l >= r) return;
int i = l - 1, j = r + 1, x = q[(l + r) / 2];
while (i < j){
do i++; while (q[i] < x);
do j--; while (q[j] > x);
if (i < j) swap(q[i], q[j]);
}
quick_sort(q, l, j), quick_sort(q, j + 1, r);
}
int main() {
int n;
cin >> n;
int array[100];
for (int i = 0; i < 2 * n; i++)cin >> array[i];
quick_sort(array, 0, 2 * n - 1);
int center = (2 * n - 1) / 2;
cout << array[center] << endl;
}题目六:DS静态查找 -- 链表的有序构建和查找
题目描述:
单链表结点的存储结构包含两部分:数据、下一结点指针(默认为空)。
单链表包含头结点,存储实际数据的结点位置从1开始。
现输入一批无序的整数队列,编写程序完成以下要求
1)构建单链表并且把数据按递增顺序插入到链表中,并且统计非空指针发生变化的次数。
例如在初始只包含头结点的单链表中,依次插入3和2
当把3插入时,是头结点的next指针发生变化,初始头结点的next指针是空的,现在指向3的结点,所以不计入指针变化次数。
当把2插入时,它是插入到头结点和3结点之间,这时候头结点的next指针从指向3变成指向2,因此这次计入指针变化次数。
总之,如果是把一个空的next指针指向新的结点,则不计入变化次数;如果是把一个非空next指针修改指向新结点则计入变化次数。
2)实现对单链表的元素查找。输入一个链表位置,返回该位置对应的数据。如果位置非法则输出提示信息,看样例。
要求:必须使用单链表结构实现上述要求,并且不能用第三方算法库或容器类对象
输入要求:
第一行:第一个数字n表示样本数目,其后跟n个样本。
第二行:查找测试次数m 后跟m个待查找的位置。
输出要求:
第一行输出构建链表过程中,非空指针变化的总次数,格式看样本
第二行输出单链表创建后,从头到尾依次输出链表中元素数据
第三行到第n+1行,对每个查找位置,若结点存在,输出结点数据;否则输出error
输入样例:
6 1 8 5 2 4 3
4 0 2 10 6
输出样例:
非空指针变化4次
1 2 3 4 5 8
error
2
error
8代码示例:
#include<iostream>
#include<cmath>
#include<iomanip>
#include<algorithm>
#include<cstring>
using namespace std;
struct Node {
int data;
Node* next;
Node() :data(-1), next(nullptr) {}
Node(int e) :data(e), next(nullptr) {}
};
class list {
private:
int num = 0;
Node* head;
int size;
public:
list() {
size = 0;
head = new Node();
}
~list() {}
void Insert(int x) {
Node* tmp = new Node(x);
Node* s;
s = head;
while (1) {
if (s->next == NULL) {
s->next = tmp;
break;
}
if (s->next->data > x) {
num++;
tmp->next = s->next;
s->next = tmp;
break;
}
s = s->next;
}
size++;
}
void Display() {
Node* s;
s = head;
for (int i = 0; i < size - 1; i++) {
s = s->next;
cout << s->data << " ";
}
s = s->next;
cout << s->data << endl;
}
int Find(int x) {
Node* s;
s = head;
if (x > size) return -1;
else {
for (int i = 0; i < x; i++) s = s->next;
return s->data;
}
}
int getNum() { return num; }
};
int main() {
int n;
cin >> n;
list l;
int x;
while (n--) {
cin >> x;
l.Insert(x);
}
cout << "非空指针变化" << l.getNum() << "次" << endl;
l.Display();
int m, result;
cin >> m;
for (int i = 0; i < m; i++) {
cin >> x;
result = l.Find(x);
if (result == -1) cout << "error" << endl;
else cout << result << endl;
}
return 0;
}