1.做题链接：. - 力扣（LeetCode）

2.做题前须：

两数之和降低复杂度：

1.问题描述：一个数组中找到两个数字之和是taeget

例如：[2,7,11,15,19,21],target=30

2.解法一：暴力枚举时间复杂度为O(n^2)放心力扣绝对不会让你过的

解法二：双指针+单调性时间复杂度是O(n)

第一步：先排序

第二步：利用单调性来找出答案，建议大家多画几遍

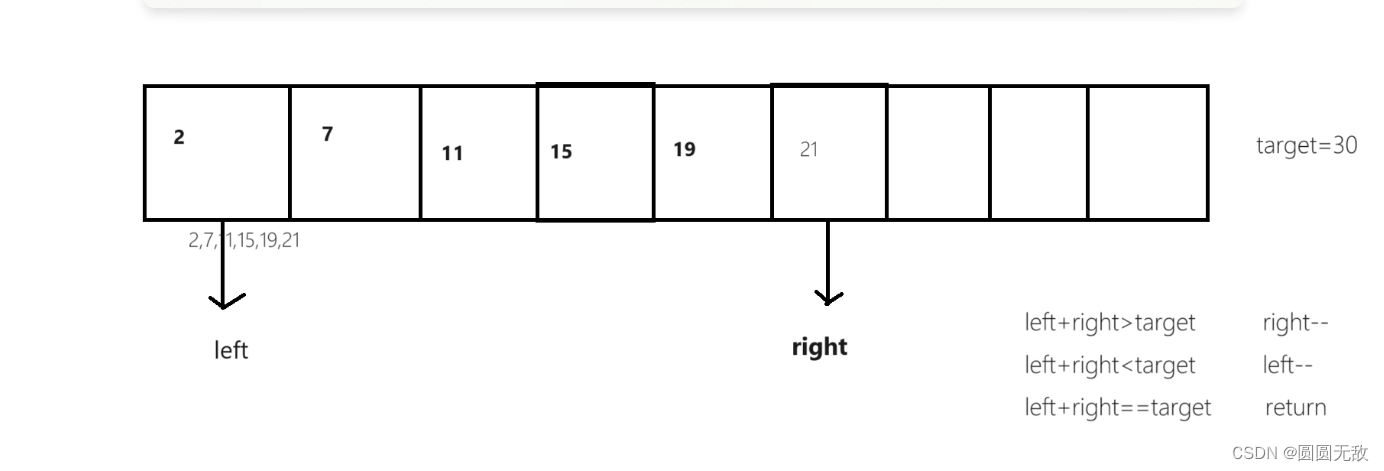
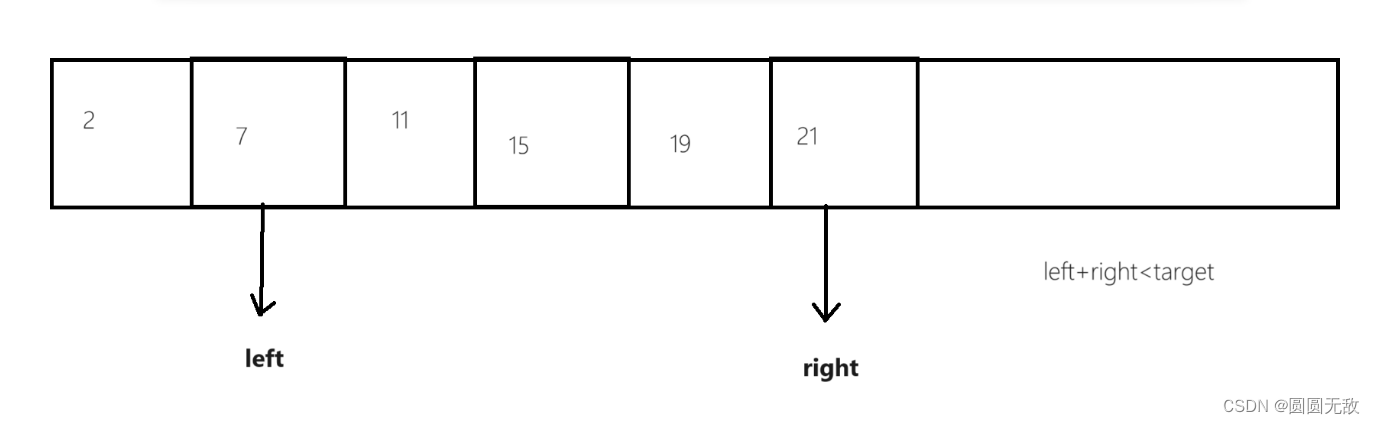
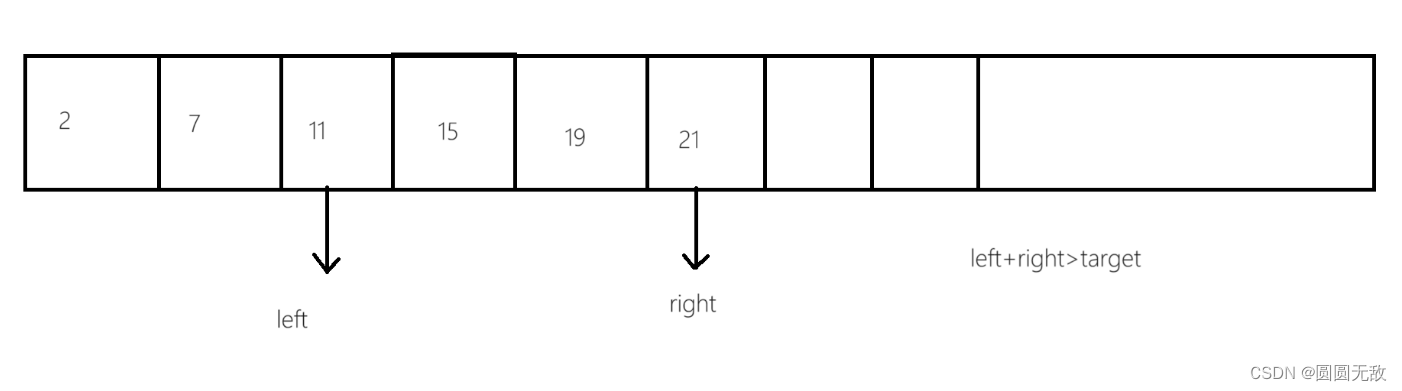
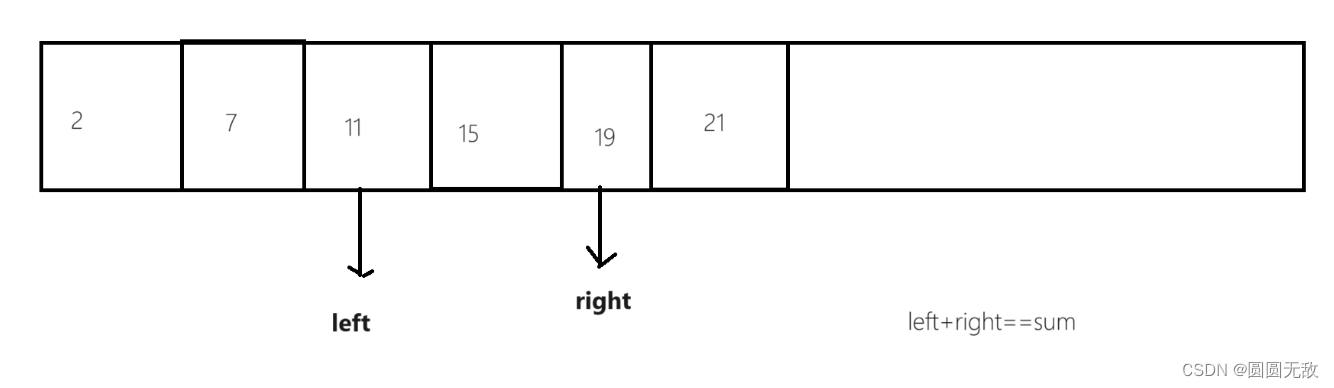第三步：编写代码

public int[] ways(int[] nums,int target)
    {
        if(nums.length<=0)
        {
            return new int[]{};
        }
        else 
        {
            int left=0;
            int right=nums.length-1 ;
            while (left<right && left<nums.length && right<nums.length)
            {
                int sum=nums[left]+nums[right];
                if(sum==target)
                {
                    return new int[]{nums[left],nums[right]};
                }
                else if(sum<target && left<nums.length)
                {
                    left++;
                }
                else if(sum>target && right<nums.length)
                {
                    right--;
                }
            }
        }
        return new int[]{};
    }

3.开始正式做题

1.分析题目：

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请

你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

得出结论： nums[i]+nums[j]+nums[k]==0 && i!=k!=j;

2.算法原理：

1.暴力枚举：显然是不行的都O(n^3)，力扣肯定顶过不了，通过上面的阐述，我们可以将三个数返程1+2的形式：将一个指针i指向数组的元素，然后用target去减去nums[i]的到两个数的target然后转化成求两数之和这个就是解法二

2解法二：单调性，双指针加上暴力枚举，时间复杂度降到O(n^2)

主题步骤：

1.先排序：有冒泡，选择，堆排序，归并排序，快速排序等

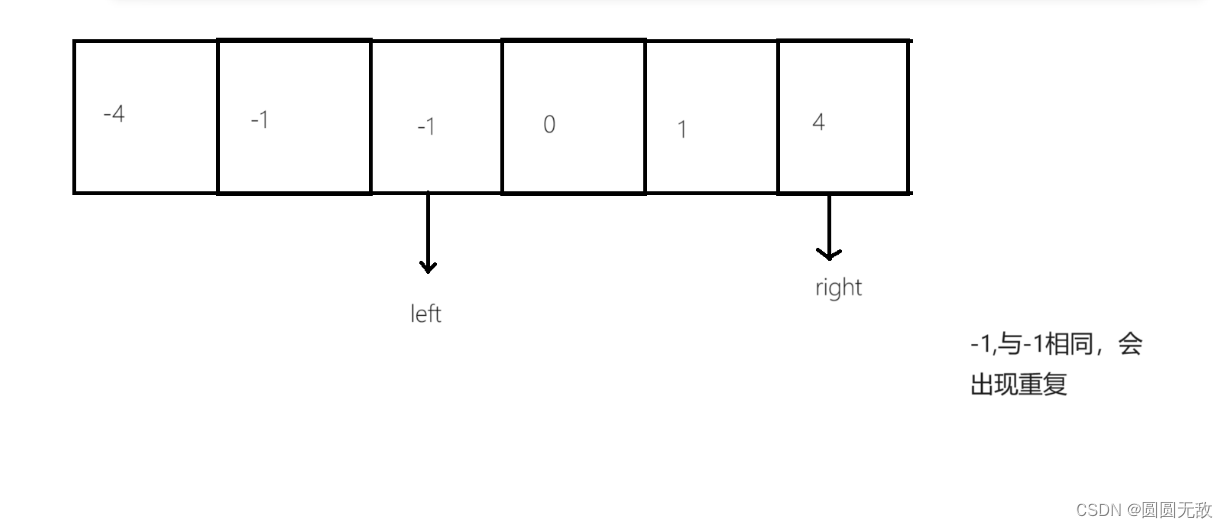
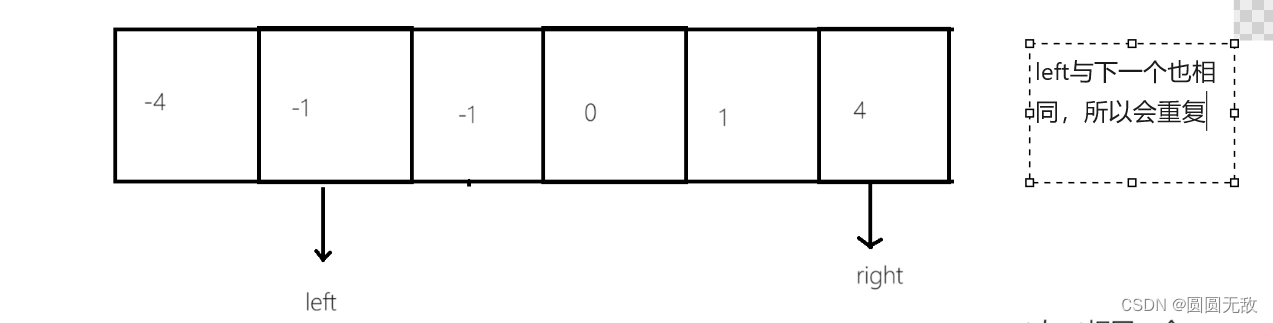
2.去重：避免重复，我们要注意两个点：

指定数nums[i]和上一个相同

left 与right和上一个相同

3.避免遗漏

再找到后只要left<right就还可以找

代码编写：

public static List<List<Integer>> threeSum(int[] nums) {
        if(nums.length==0)
        {
            return null;
        }
        List<List<Integer>> sum=new ArrayList<>();
        Arrays.sort(nums);
        for(int i=0;i<nums.length;i++)
        {
            if (i!=0 && nums[i-1]==nums[i])
            {
                continue;
            }
            int left=i+1;
            int right=nums.length-1;
            int target=0-nums[i];
            while (left<right && left<nums.length && right<nums.length)
            {
                if(nums[left]+nums[right]==target)
                {
                    List<Integer>num=new ArrayList<>();
                    num.add(nums[i]);
                    num.add(nums[left]);
                    num.add(nums[right]);
                    sum.add(num);
                    while (left<nums.length && nums[left]==num.get(1))
                    {
                        left++;
                    }
                    while (right>0 && nums[right]==num.get(2))
                    {
                        right--;
                    }

                }
                else if(nums[left]+nums[right]<target && left<nums.length)
                {
                    left++;
                }
                else if(nums[left]+nums[right]>target && right<nums.length)
                {
                    right--;
                }
            }
        }
        return sum;
    }