一、介绍
在时间序列分析中,通常需要通过考虑先前的值来了解序列的趋势方向。序列中下一个值的近似可以通过多种方式执行,包括使用简单基线或构建高级机器学习模型。
指数(加权)移动平均线是这两种方法之间的稳健权衡。在幕后有一个简单的递归方法可以有效地实现该算法。同时,它非常灵活,可以成功适应大多数类型的序列。
本文介绍了该方法背后的动机、其工作流程和偏差校正的描述——一种克服近似中偏差障碍的有效技术。
二、动机
想象一个近似随时间变化的给定参数的问题。在每次迭代中,我们都知道它之前的所有值。目标是根据先前的值来预测下一个值。
一种幼稚的策略是简单地取最后几个值的平均值。这在某些情况下可能有效,但不太适合参数更依赖于最新值的情况。
克服此问题的可能方法之一是将较高的权重分配给较新的值,并将较少的权重分配给先前的值。指数移动平均线正是遵循这一原则的策略。它基于这样的假设:变量的较新值比先前值对下一个值的形成贡献更大。
三、公式
为了理解指数移动平均线的工作原理,让我们看看它的递归方程:
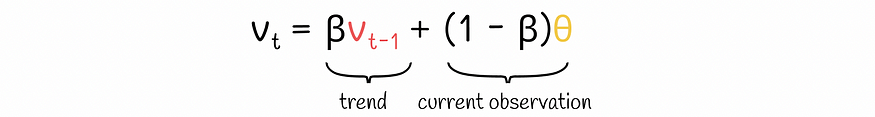
指数移动平均公式
- vₜ 是近似给定变量的时间序列。它的索引 t 对应于时间戳 t。由于该公式是递归的,因此需要初始时间戳 t = 0 的值 v₀。实际中,v₀通常取0。
- θ 是当前迭代的观测值。
- β 是一个介于 0 和 1 之间的超参数,定义权重重要性应如何在先前平均值 vₜ-₁ 和当前观测值 θ 之间分布
让我们为前几个参数值写下这个公式:

第t个时间戳的获取公式
结果,最终的公式如下所示:

第 t 个时间戳的指数移动平均值
我们可以看到,最近的观测值 θ 的权重为 1,倒数第二个观测值 — β,倒数第三个 — β² 等。由于 0 < β < 1,乘法项 βᵏ 随着 k 的增加呈指数下降,因此,观察结果越旧,它们就越不重要。最后,将每个总和项乘以 (1 -β)。
实际上,β 的值通常选择接近 0.9。
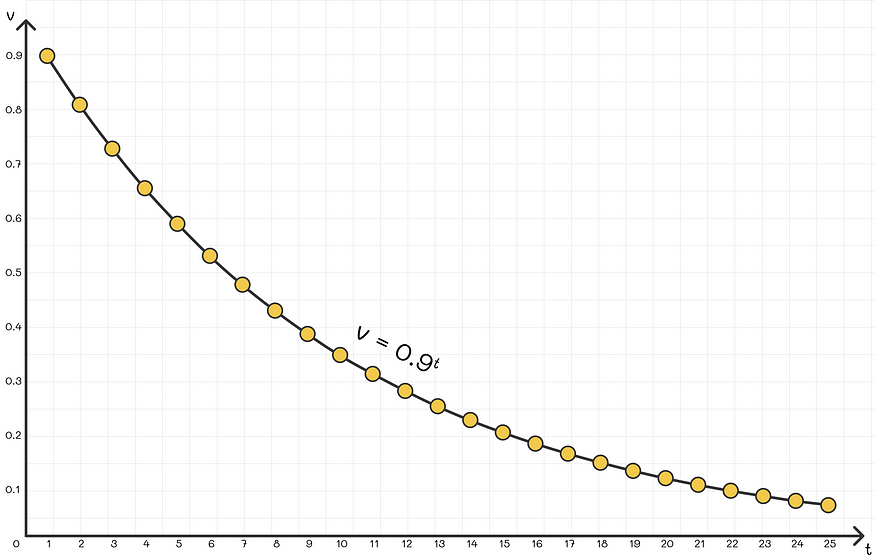
不同时间戳的权重分布(β = 0.9)
四、数学解释
利用数学分析中著名的第二奇妙极限,可以证明以下极限:

通过替换 β = 1 - x,我们可以将其重写为以下形式:
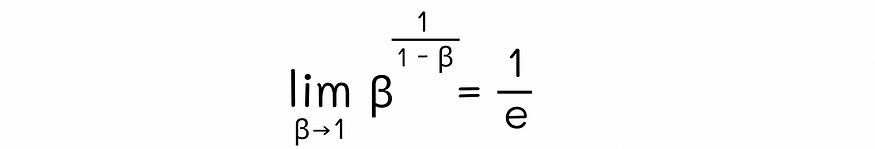
我们还知道,在指数移动平均值的方程中,每个观测值都乘以项 βᵏ,其中 k 表示计算观测值之前的时间戳。由于两种情况下的底数 β 相等,因此我们可以使两个公式的指数相等:
通过使用这个方程,对于选定的 β 值,我们可以计算权重项达到值 1 / e ≈ 0.368 所需的时间戳 t 的近似数量。这意味着在最后 t 次迭代中计算的观测值具有大于 1 / e 的权重项,而在最后 t 次时间戳范围内计算出的更先例的权重项则低于 1 / e,其重要性要小得多。
实际上,低于 1 / e 的权重对指数加权平均值的影响很小。这就是为什么说对于给定的 β 值,指数加权平均值会考虑最后 t = 1 / (1 - β) 观测值。
为了更好地理解该公式,让我们为 β 代入不同的值:

例如,取 β = 0.9 表示大约在 t = 10 次迭代中,与当前观测值的权重相比,权重衰减至 1 / e。换句话说,指数加权平均值主要取决于最后 t = 10 个观测值。
五、偏差校正
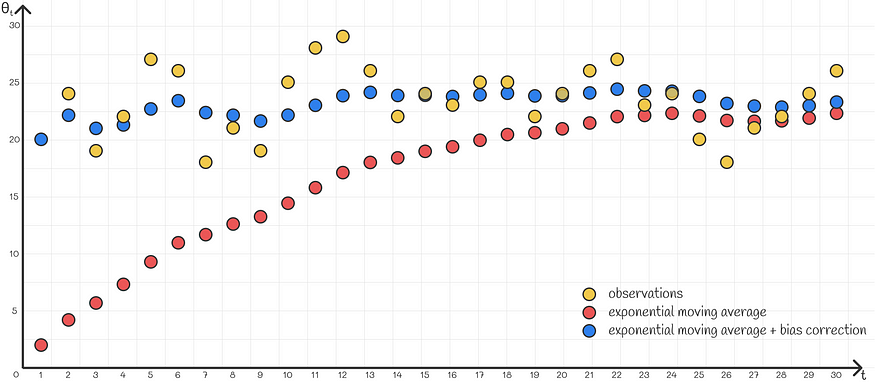
使用指数加权平均值的常见问题是,在大多数问题中,它不能很好地近似第一个系列值。发生这种情况的原因是第一次迭代时缺乏足够的数据。例如,假设我们给出以下时间序列:
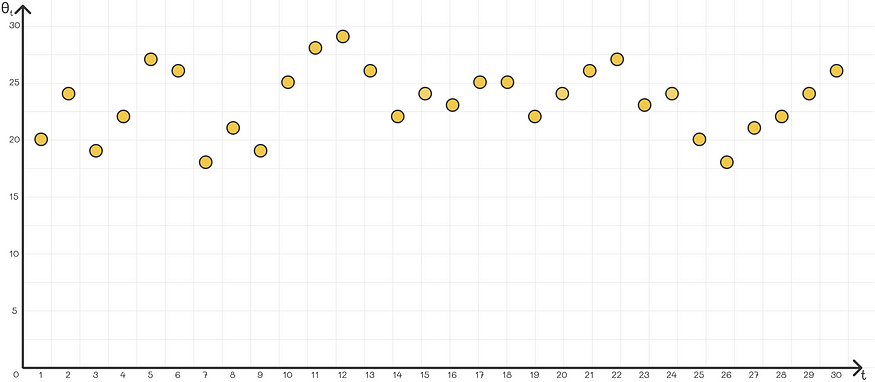
目标是用指数加权平均值来近似它。然而,如果我们使用正常公式,那么前几个值将对 v₀ 施加很大的权重,即 0,而散点图上的大多数点都在 20 以上。因此,第一个加权平均值的序列将太低精确地近似原始序列。
其中一个简单的解决方案是采用接近第一个观测值 θ1 的 v0 值。尽管这种方法在某些情况下效果很好,但它仍然不完美,特别是在给定序列不稳定的情况下。例如,如果 θ2 与 θ1 差异太大,则在计算第二个值 v2 时,加权平均值通常会比当前观测值 θ2 更重视先前趋势 v1。结果,近似值将非常差。
一种更灵活的解决方案是使用一种称为“偏差校正”的技术。它们不是简单地使用计算值 vₖ,而是除以 (1 —βᵏ)。假设选择的 β 接近 0.9-1,则对于 k 较小的第一次迭代,该表达式趋于接近 0。因此,现在不是慢慢累加 v₀ = 0 的前几个值,而是将它们除以相对较小的数字,将它们缩放为更大的值。
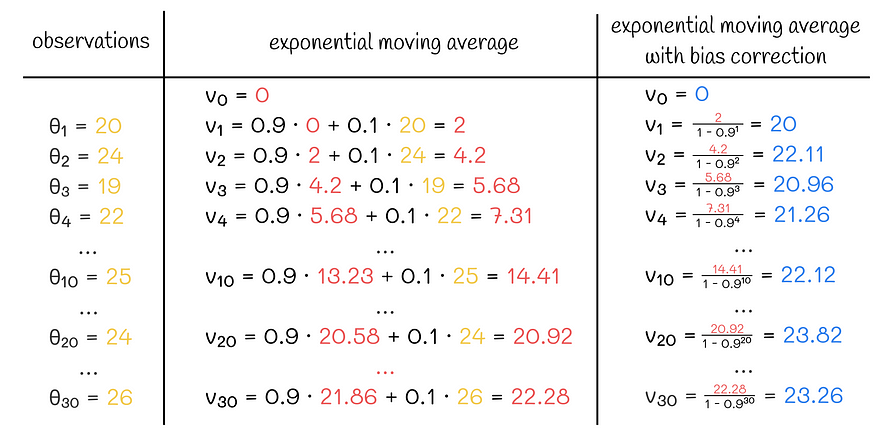
带和不带偏差校正的指数移动平均计算示例
一般来说,这种缩放效果非常好,并且精确地适应了前几项。当k变大时,分母逐渐接近1,从而逐渐忽略不再需要的这种缩放的影响,因为从某个迭代开始,算法可以高度可信地依赖其最近的值,而无需任何额外的缩放。
六、结论
在本文中,我们介绍了一种非常有用的近似时间序列序列的技术。指数加权平均算法的鲁棒性主要是通过其超参数β来实现的,β可以适应特定类型的序列。除此之外,引入的偏差校正机制使得即使在信息太少的早期时间戳上也可以有效地近似数据。
指数加权平均在时间序列分析中有着广泛的应用范围。此外,它还用于梯度下降算法的变体中以加速收敛。其中最受欢迎的之一是深度学习中的动量优化器,它消除了优化函数不必要的振荡,使其更精确地对准局部最小值。