一、前言
Medium 难度主要考察结合二叉树性质的 CRUD 操作,而这一切的基础都离不开遍历二叉树。
二叉树是图的子集,因而同样适用以下两种搜索思想:
-
**DFS(深度优先搜索):**沿着根节点递归下去,遇到叶子节点则向上回溯;
-
**BFS (广度优先搜索):**按照二叉树的层次访问,通常采用队列保存每个层次的节点。
由于二叉树本身的定义就是递归的,所以采用递归处理起来,代码更容易理解。但是递归的效率相对比较慢,主要原因在于:一个函数被调用的时间和空间成本开销很大,递归太多很可能导致调用栈溢出的问题。上一篇中也提到可以采用尾递归的书写方式,让 JavaScript 引擎去将递归优化成迭代,从而解决性能上的问题。
但是在一些情况下,尾递归并没有那么好写,所以本文会同时给出递归和迭代的解决方案。
接下来,通过具体的题目解析,带大家了解 DFS 和 BFS 搜索思想在二叉树中的应用。
二、102. 二叉树的层次遍历
给定一个二叉树,返回其按层次遍历的节点值。(即逐层地,从左到右访问所有节点)。
1、BFS
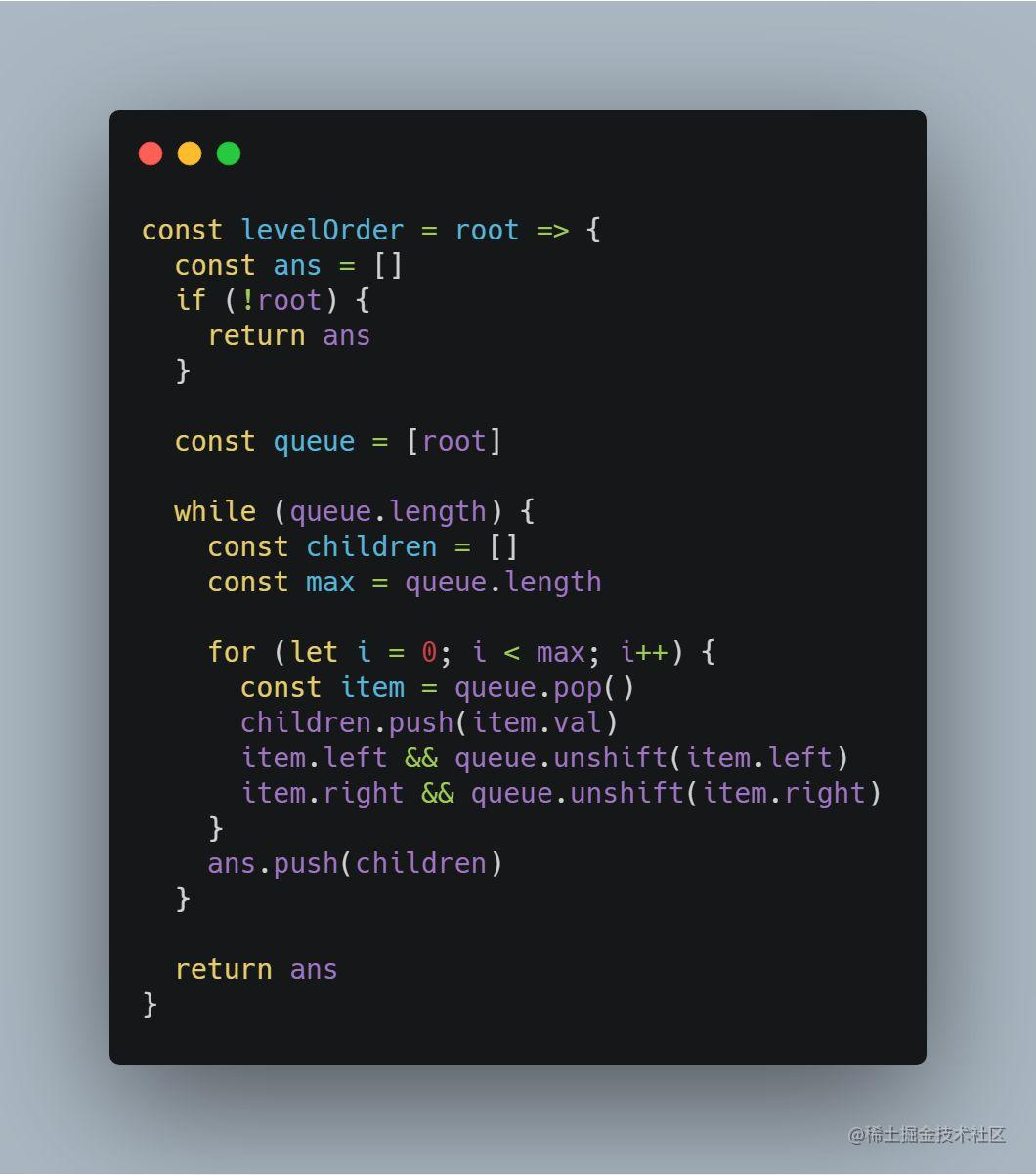
这道题目要求按层次遍历节点,很符合 BFS 搜索思想的定义,所以代码也很好理解。
这里需要利用队列(queue)来保存每一层需要访问的节点,需要特别注意队列的特性是先进先出,而本题要求每一层从左到右遍历,所以需要先将左子树放入队列。
2、DFS
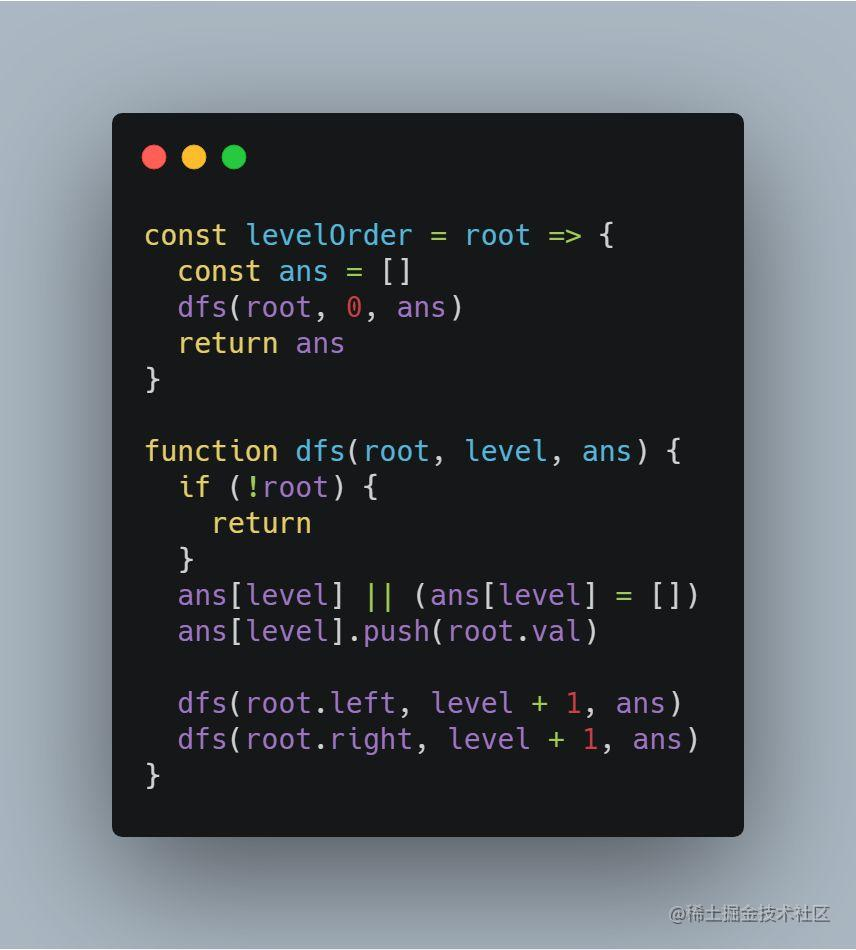
采用 DFS 搜索思想,需要注意在递归的过程中记录当前节点的层次信息:
三、145. 二叉树的后序遍历
给定一个二叉树,返回它的 后序 遍历。
二叉树中最常见的就是按照根节点访问次序定义的三种遍历方式:
-
先序遍历:首先访问根,再先序遍历遍历左子树,最后先序遍历右子树;
-
中序遍历:首先中序遍历左子树,再访问根,最后中序遍历右子树;
-
后序遍历:首先后序遍历左子树,再后序遍历右子树,最后访问根;
以本道题的后序遍历为例,尝试递归和迭代两种不同的方法:
1、递归实现 DFS
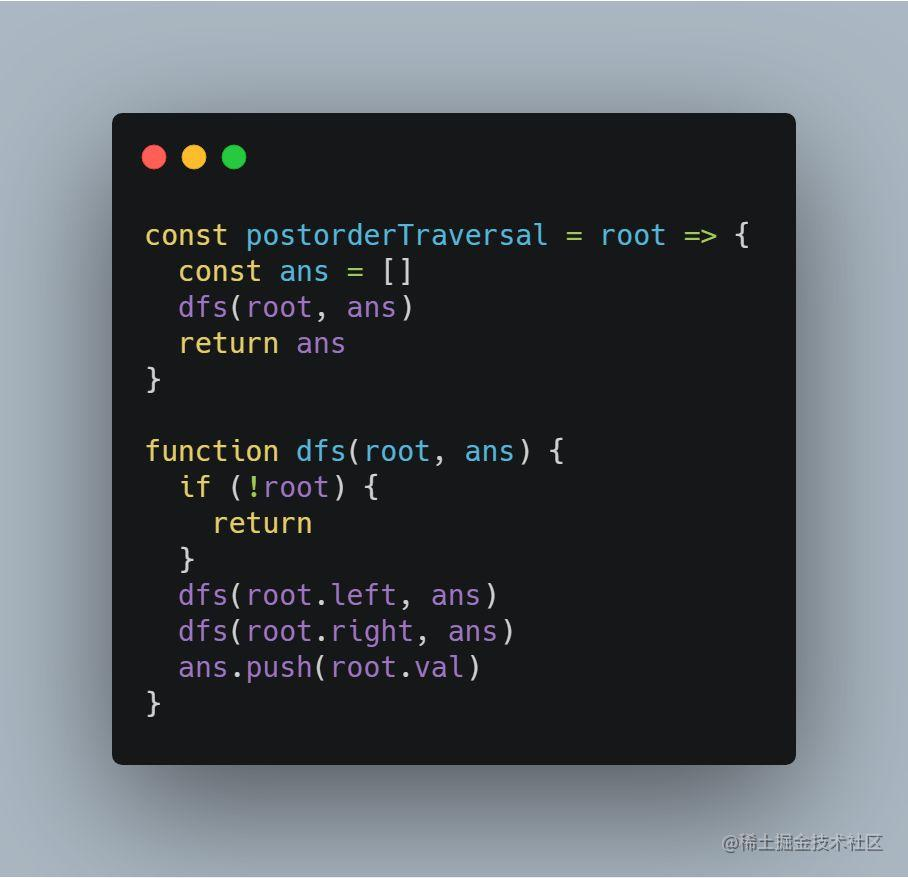
从定义中,大家应该能够想象到递归的代码如何书写:
参考视频:传送门
2、迭代实现 DFS
本道题目采用迭代实现 DFS 不太容易理解,主要由于迭代不能像递归那样向上回溯,所以迭代向下遍历的过程中,无法保证根节点最后访问。
再回顾一下后序遍历最终得到的序列:
左子树 --> 右子树 --> 根
如果必须先访问根节点,那么是不是可以得到这样的序列:
根 --> 右子树 --> 左子树
最后,再将该序列反转,是不是就是本题所要求解的后序遍历!
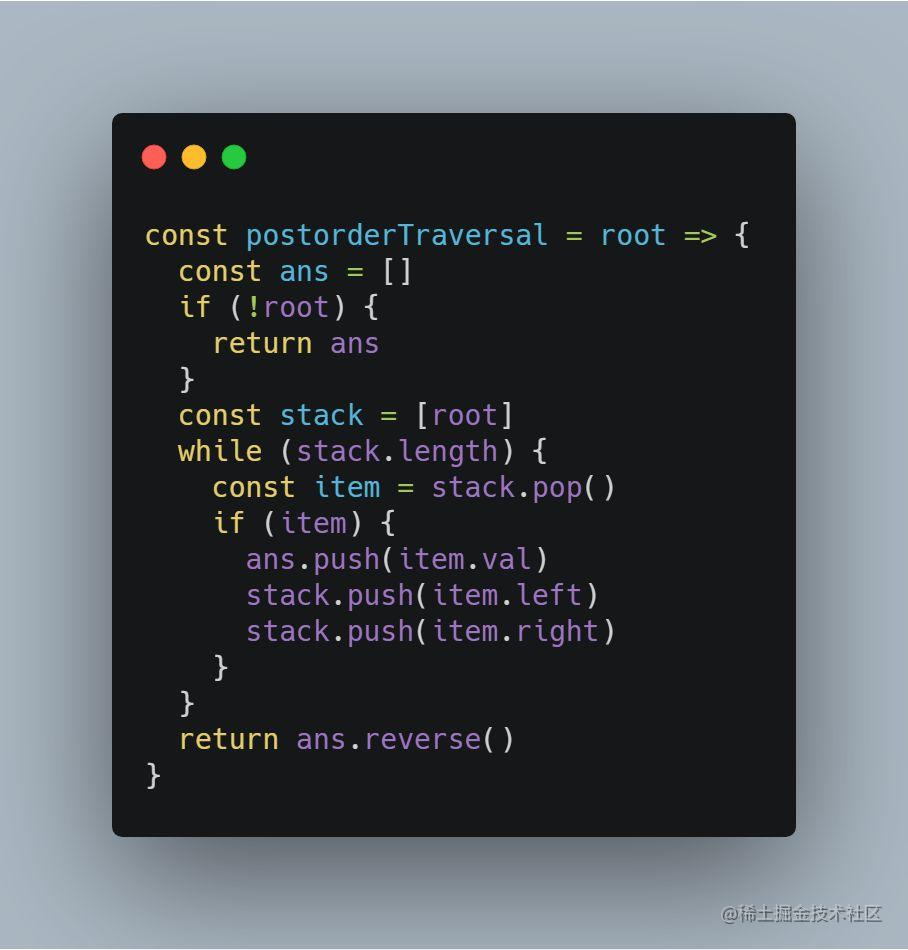
这里我们利用栈后进先出的特性,将右子树最后推进栈,使得右子树先进行深度搜索:
四、987. 二叉树的垂序遍历
给定二叉树,按垂序遍历返回其结点值。对位于 (X, Y) 的每个结点而言,其左右子结点分别位于 (X-1, Y-1) 和 (X+1, Y-1)。把一条垂线从 X = -infinity 移动到 X = +infinity ,每当该垂线与结点接触时,我们按从上到下的顺序报告结点的值( Y 坐标递减)。如果两个结点位置相同,则首先报告的结点值较小。按 X 坐标顺序返回非空报告的列表。每个报告都有一个结点值列表。
最后,通过本道题目来开启 Medium 难度题型的讲解。
这道题目要求我们求出垂序遍历序列,那么首先还是得先遍历二叉树,这里采用递归实现 DFS 来遍历二叉树。
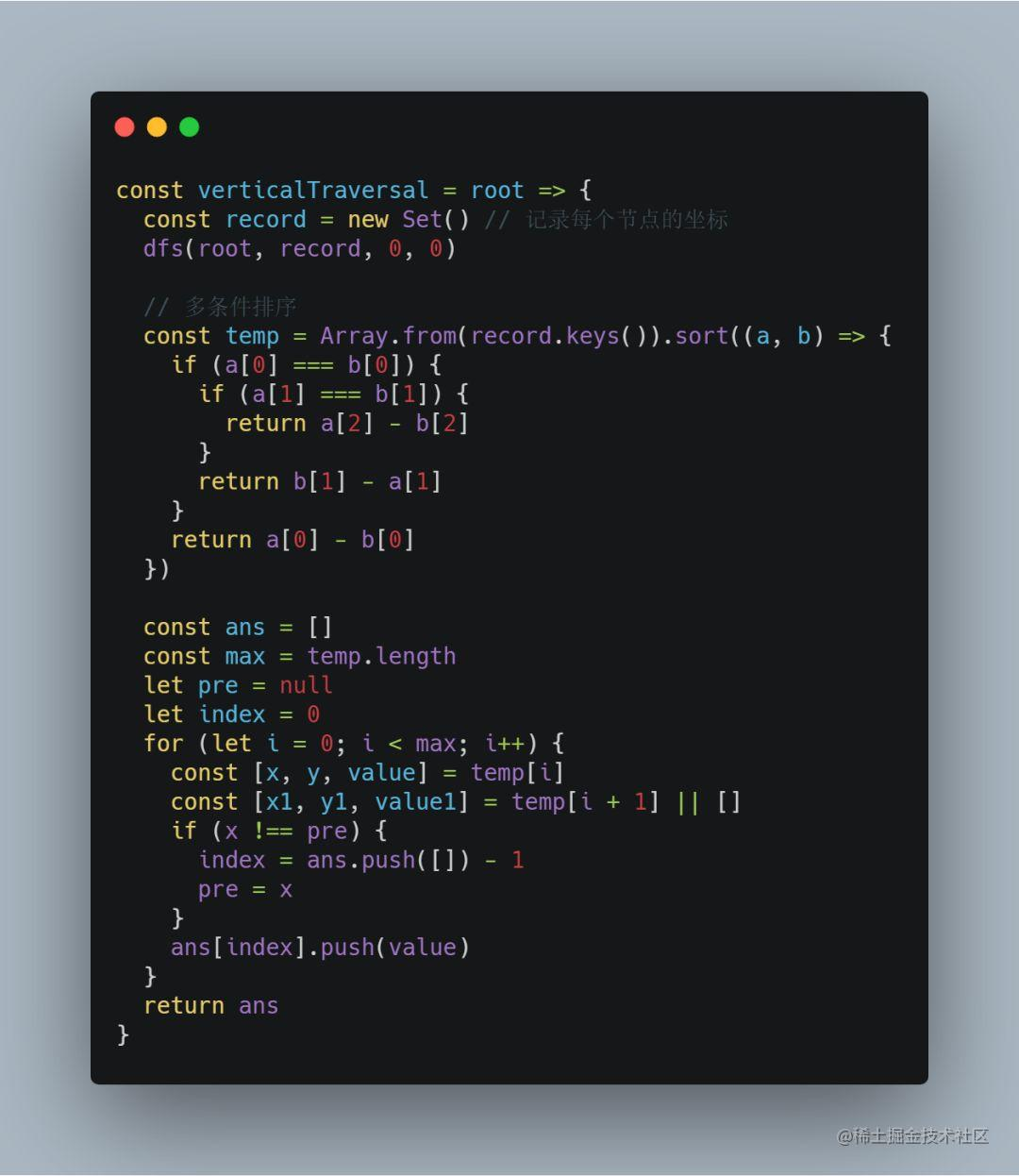
在递归的过程中需要向下传递坐标信息,并且通过 HashTable 记录各个节点的三元组信息( x 坐标、y 坐标,节点值),以便后续构造垂序序列:

得到坐标之后,需要对三元组进行综合排序,最后再根据 x 坐标构造垂序遍历序列,时间复杂度 O(nlogn)。
写在最后
算法作为计算机的基础学科,用 JavaScript 刷,一点也不丢人ε=ε=ε=┏(゜ロ゜;)┛。
本系列文章会分别给出一种算法的3种难度的总结篇(简单难度,中等难度以及困难难度)。在简单难度中,会介绍该算法的基本知识与实现,另外两个难度,着重讲解解题的思路。
如果本文对您有所帮助,可以点赞或者关注来鼓励博主。