一、区间问题1：最大不相交区间数量

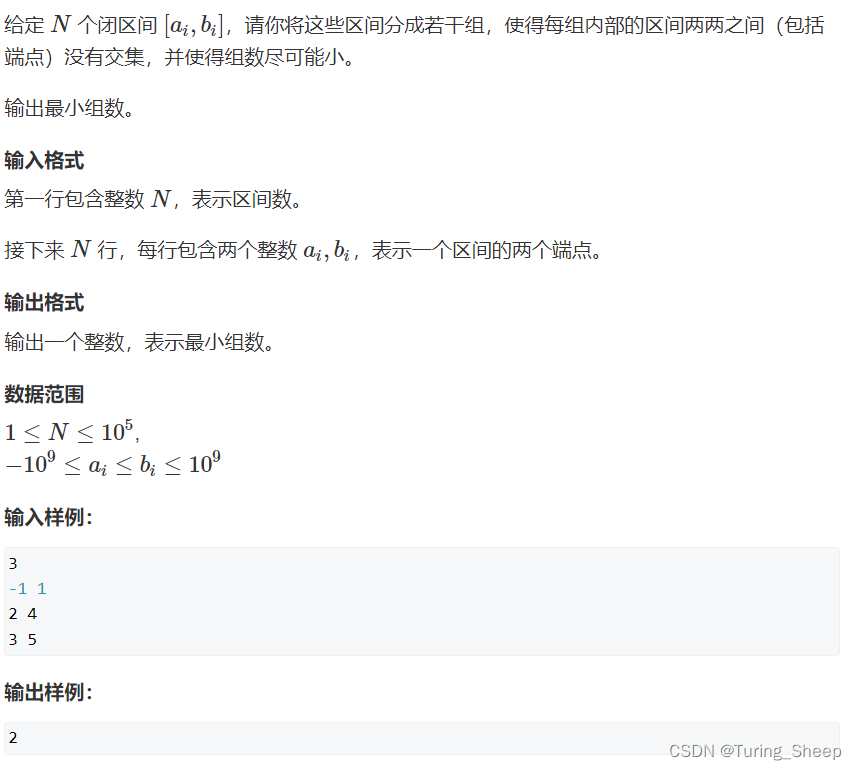
1、思路详解

这道题和前一章讲的最后一道题思路非常的相似，如果大家没看过那篇文章的话，作者建议先去看看那篇：
传送门：贪心算法——区间问题（上）

步骤：

1、将所有区间按左端点从小到大排序
2、从前往后处理每个区间判断能够将其放到某个现有的组中，即判断当前组内最靠左的左端点和前一个组最靠右的右端点之间关系：L[i]和Max_r之间的关系。
（1）如果存在这样的组，即L[i]>Max_r，说明可以把当前的区间放到这个组中，但是由于我们加入了一个新的区间所以要更新一下右端点的最大值。由于我们的L[i]>Max_r，那么加入之后的r[i]一定大于Max_r。所以，这个Max_r删掉即可。
（2）如果不存在这样的组，就让它成为一个新的组。

由于我们判断的是是否存在。因此，我们需要在所有组的Max_r之中选出一个最小值，记作Mr_min。如果L[i]<Mr_min的话，那么必定是不存在的。反之则存在。故我们可以采用小根堆。

2、代码实现

#include<iostream>
#include<vector>
#include<algorithm>
#include<queue>
using namespace std;
int n;
vector<pair<int,int>>a;
int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
    {
        int l,r;
        scanf("%d%d",&l,&r);
        a.push_back({l,r});
    }
    sort(a.begin(),a.end());
    priority_queue<int,vector<int>,greater<int>>max_r;
    for(int i=0;i<n;i++)
    {
        if(!max_r.size())
        {
            max_r.push(a[i].second);
            continue;
        }
        if(max_r.top()>=a[i].first)max_r.push(a[i].second);
        else 
        {
            max_r.pop();
            max_r.push(a[i].second);
        }
    }
    cout<<max_r.size()<<endl;
    return 0;
}

二、区间问题2：区间覆盖

1、问题

2、思路

步骤：
1、按照左端点从小到大排序
2、从前往后依次枚举每一个区间，在所有能覆盖目标区间左端点的区间当中选择一个右端点最大的区间。选完之后，我们的第二次选择为了和上次选择的区间之间不出现断档，那么就必须保证第二个区间的左端点是大于第一次选择的区间的右端点的。后续过程也是一样。

3、代码

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int main()
{
    vector<pair<int,int>>a;
    int start,end;
    cin>>start>>end;
    int n;
    cin>>n;
    for(int i=0;i<n;i++)
    {
        int l,r;
        scanf("%d%d",&l,&r);
        a.push_back({l,r});
    }
    sort(a.begin(),a.end());
    int res=0;
    for(int i=0;i<n;i++)
    {
        int max_r=-2e9;
        int j;
        for( j=i;j<n;j++)
        {
            if(a[j].first<=start)
            {
                max_r=max(a[j].second,max_r);
            }
            else
                break;
        }
        if(max_r==-2e9)
        {
            cout<<-1<<endl;
            return 0;
        }
        start=max_r;
        res++;
        i=j-1;
        if(max_r>=end)
        {
            cout<<res<<endl;
            return 0;
        }
    }
    cout<<-1<<endl;
}