🌳🌳🌳小谈:一直想整理机器学习的相关笔记,但是一直在推脱,今天发现知识快忘却了(虽然学的也不是那么深),但还是浅浅整理一下吧,便于以后重新学习。
📙参考:ysu期末复习资料和老师的课件
1.回归问题
回归分析用于预测输入变量(自变量)和输出变量(因变量)之间的关系,特别是当输入变量的值发生变化时,输出变量值随之发生变化。
🍀理解:直观来说回归问题等价于函数拟合,选择一条函数曲线使其很好地拟合已知数据且很好地预测未知数据。
回归分析根据自变量个数可分为一元回归分析与多元回归分析。

2.一元线性回归
线性回归算法假设特征和结果满足线性关系。
这就意味着可以将输入项分别乘以一些常量,再与偏置项相加得到输出。
一元线性回归指的是分析只有一个自变量x与因变量y线性相关关系的方法。
过程如下:

举个例子:
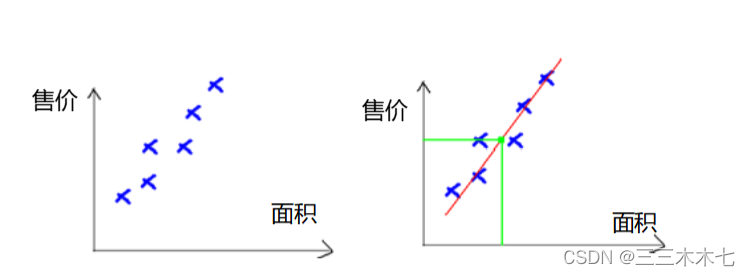
左图是以面积为X轴,售价为Y轴建立房屋销售数据的特征空间表示图。
回归分析是:用一条曲线去尽量准的拟合这些数据,然后如果有新的输入过来,我们可以在将曲线上这个点对应的值返回。
3.一元线性回归求解方法
3.1 最小二乘法
最小二乘法的主要思想:就是求解未知参数,使得理论值与观测值之差(即误差,或者说残差)的平方和达到最小。
【所谓最小二乘,其实也可以叫做最小平方和,其目的就是通过最小化误差的平方和,使得拟合对象无限接近目标对象。】
缺点:最小二乘法主要针对于线性函数,有全局最优解且是闭式解,针对更加复杂的函数难起作用
3.2 梯度下降法
梯度下降法是用来计算函数最小值的。
根据计算一次目标函数梯度的样本数量可分为批量梯度下降(Batch graduebt descent, BGD),随机梯度下降(Stochatic gradient decent, SGD),小批量梯度下降(mini-batch gradient descent)。
(1)批量梯度下降 BGD
在训练过程中,每一步迭代都使用训练集的所有内容。
也就是说,利用现有参数对训练集中的每一个输入生成一个估计输出y ̂_i,然后跟实际输出 y_i 比较,统计所有误差,求平均以后得到平均误差,以此来作为更新参数的依据。
优点:由于每一步都利用了训练集中的所有数据,因此当损失函数达到最小值以后,能够保证此时计算出的梯度为0,换句话说,就是能够收敛。因此,使用BGD时不需要逐渐减小学习速率。
缺点:由于每一步都要使用所有数据,因此随着数据集的增大,运行速度会越来越慢.
(2)随机梯度下降 SGD
随机梯度下降方法一次只抽取一个随机样本进行目标函数梯度计算。
优点:由于每次只计算一个样本,所以SGD收敛非常快。
缺点:因为是随机抽取样本,因此误差是不可避免的,且每次迭代的梯度受抽样的影响比较大。
(3)小批量梯度下降 mini-batch GD
小批量梯度下降结合了批量梯度下降和随机梯度下降的优点,它一次以小批量的训练数据计算目标函数的权重并更新参数。
🌍梯度下降法的问题
1. 难以选择合适的学习速率:如果学习速率选择过小会造成网络收敛太慢,但是设得太大可能使得损失函数在最小点周围不断摇摆而永远达不到最小点;
2.如果训练数据十分稀疏并且不同特征的变化频率差别很大,这时候对变化频率慢得特征采用大的学习率,而对变化频率快的特征采用小的学习率是更好的选择;
3.3 梯度下降改进
(1)Momentum
若当前的梯度方向与累积的历史梯度方向一致,则当前的梯度会被加强,从而这一步下降的幅度更大。若当前的梯度方向与累积的梯度方向不一致,则会减弱当前下降的梯度幅度。
(2)AdaGrad(Adaptive Gradient)
每一次更新参数时(一次迭代),不同的参数使用不同的学习率。
(3)Adam( Adaptive Moment Estimation)
Adam利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。其优点主要在于经过偏置校正后,每一次迭代学习率都有个确定范围,使得参数比较平稳。
4.损失函数
1.平均绝对误差:平均绝对误差MAE(Mean Absolute Error)又被称为l1范数损失(l1-norm loss)
2.平均平方误差:平均平方误差MSE(Mean Squared Error)又被称为l2范数损失(l2-norm loss):
3.均方根差RMSE:是MSE的算术平方根
5.线性回归的改进
5.1 过拟合
过拟合是指模型学习的参数过多,导致拟合的函数完美的预测训练集,但对新数据的测试集预测结果差。
解决办法:
(1)获取更多的数据
(2)数据增强(Data Augmentation)
通过一定规则扩充数据。
(3)使用合适的模型:
减少网络的层数、神经元个数等均可以限制网络的拟合能力;
(4)使用正则项约束模型的权重,降低模型的非线性。
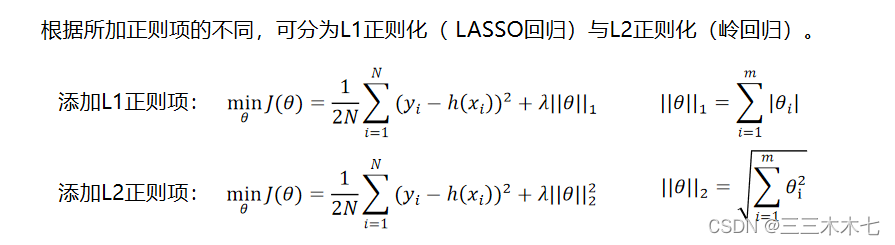
6.项目实战
6.1 波士顿房价
以Scikit-learn的内置数据集波士顿(Boston)房屋价格为案例,采用单变量线性回归算法对数据进行拟合与预测。
波士顿房屋的数据于1978年开始统计,共506个数据点,涵盖了波士顿不同郊区房屋的14种特征信息。
在这里,选取房屋价格(MEDV)、每个房屋的房间数量(RM)两个变量进行回归,其中房屋价格为目标变量,每个房屋的房间数量为特征变量。将数据导入进来,并进行初步分析。
机器学习基本步骤:
数据预处理→特征工程→数据建模→结果评估
💬
🍨🍄🍬🍺🍹🍸🥤🍷🍥📙
🌸🌸🍔🥪🍟
🌸
🌸
🌸🌸🌸🌸🌸🌸🌸🌸
🌼🌻🍨🦄🌰
🌸🍀🌟🌵🌻👣👣🍧🍬🍡🌾🎄🌳🌴🌱☘🌳🍇🍎
🔥
🍀🌹🌍🌎🌏💪💎💰🌈🌏⚡🌟💫☀️⭐🌙🌛💦💤☔🌂💯🍋🥭🍓🥒🥠🍇✩🌕🍊👉🧁
🌸🍞🍭🍧🌹🥀🌷💐🌸🍀☘️🌲🏵️🍂🎍🌴🌳🌵🎋🍃🍁🌾
🌟☄
🐳自我总结:
💬一起加油!