期末考试临近,每天复习一点知识,还是可以复习完的,加油
前言
我后来才知道这是力扣上的一道题,我当时写他的时候名字叫找到单身狗,即使那个只出现了一次的数字
题目
136. 只出现一次的数字
给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。

题目
所谓单身狗问题翻译成数学问题就是在已知的一串数字,有一个数字只出现一次,其余的出现两次,现在你要找到是哪个数是单身狗
解析
一.一条单身狗
我们要用到按位操作符
首先异或表示当两个数的二进制表示,进行异或运算时,当前位的两个二进制表示不同则为1 ,相同则为0.
即:
0 ^ 0 = 0 ,
0 ^ 1 = 1,
1 ^ 0 = 1 ,
1 ^ 1 = 0 ,
按位异或的2个特点:
- 0 ^ 0 = 0 , 0 ^ 1 = 1, 可以发现0异或a=a。
- 任何数异或自己 = 把自己置0。
而除了单身狗其它数都是两个数那么我们知道了只要把他们一起全部进行按位异或元算就可以
例如:1 , 3 ,5,8,9,8,5,3,1
可以发现9是单身狗,则

可以发现我们要找的单身狗9出来了。
代码如下
int singleNumber(int* nums, int numsSize) {
int x = 0;
for(int i = 0; i < numsSize; i++)
x ^= nums[i];
return x;
}二.两条单身狗
可是又有一个问题出来了,如果有两条单身狗呢,那最后我们的结果就是两条单身狗的异或结果
所以我们还要进一步变换
思路:我们可以想办法把数字们分为两队,每队有一个且只有一条单身狗,然后就可俺刚才的办法写出来了
那么我们分队的标准是什么呢,就是二进制位!举个例子
1^2=3,3的二进制位时00000000 00000000 00000000 00000011
则可以知道1与2的二进制最后一位和倒数第二位是不一样的,我们就可以把最后一位二进制为1的放在一队上,是0的放在另一队上
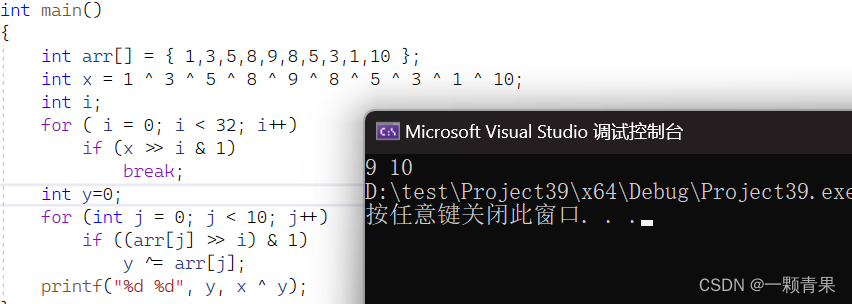
现在列出数据1 , 3 ,5,8,9,8,5,3,1,10
int x = 1 ^ 3 ^ 5 ^ 8 ^ 9 ^ 8 ^ 5 ^ 3 ^ 1^10;
int i;
for ( i = 0; i < 32; i++)
if (x >> i & 1)
break;
这样一来我们就知道按照第一位的二进制进行排队了
我们只需要在其中一个队中找到单身狗即可,因为我们已经有两个单身狗的异或了,
因为a^b^b=a,结果就出来了
ok,今天的分享就到这里了,祝大家寒假快乐,找到对象,
感觉这篇博客对你有用的话就点个赞支持一下吧!