最近公共祖先

最近公共祖先简称 LCA（Lowest Common Ancestor）。两个节点的最近公共祖先，就是这两个点的公共祖先里面，离根最远的那个。

题目链接

祖孙询问

题目描述

给定一棵包含 $n$ 个节点的有根无向树，节点编号互不相同，但不一定是 $1\sim n$。

有 $m$ 个询问，每个询问给出了一对节点的编号 $x$ 和 $y$，询问 $x$ 与 $y$ 的祖孙关系。

输入格式

输入第一行包括一个整数 $n$ 表示节点个数；

接下来 $n$ 行每行一对整数 $a$ 和 $b$，表示 $a$ 和 $b$ 之间有一条无向边。如果 $b$ 是 $-1$，那么 $a$ 就是树的根；

第 $n+2$ 行是一个整数 $m$ 表示询问个数；

接下来 $m$ 行，每行两个不同的正整数 $x$ 和 $y$，表示一个询问。

输出格式

对于每一个询问，若 $x$ 是 $y$ 的祖先则输出 $1$，若 $y$ 是 $x$ 的祖先则输出 $2$，否则输出 $0$。

数据范围

$1\le n,m\le 4\times 10^4$，$1\le$每个节点的编号$\le 4\times 10^4$

输入样例

10
234 -1
12 234
13 234
14 234
15 234
16 234
17 234
18 234
19 234
233 19
5
234 233
233 12
233 13
233 15
233 19

输出样例

1
0
0
0
2

算法思想

朴素算法

可以每次找深度比较大的那个点，让它向上跳。显然在树上，这两个点最后一定会相遇，相遇的位置就是想要求的 LCA。 或者先向上调整深度较大的点，令他们深度相同，然后再共同向上跳转，最后也一定会相遇。

朴素算法预处理时需要 dfs 整棵树，时间复杂度为 $O(n)$，单次查询时间复杂度为 $O(n)$。如果树满足随机性质，则时间复杂度与这种随机树的期望高度有关。

倍增法

倍增算法是最经典的 LCA 求法，是朴素算法的改进算法。通过预处理 $f[i][j]$ 数组，可以大幅减少了跳转次数。 $f[i][j]$ 表示点 $i$ 的第 $2^j$ 个祖先。 $f[i][j]$ 数组可以通过 dfs 预处理出来。

根据倍增思想，$f[i][j]=f[f[i][j-1]][j-1]$。

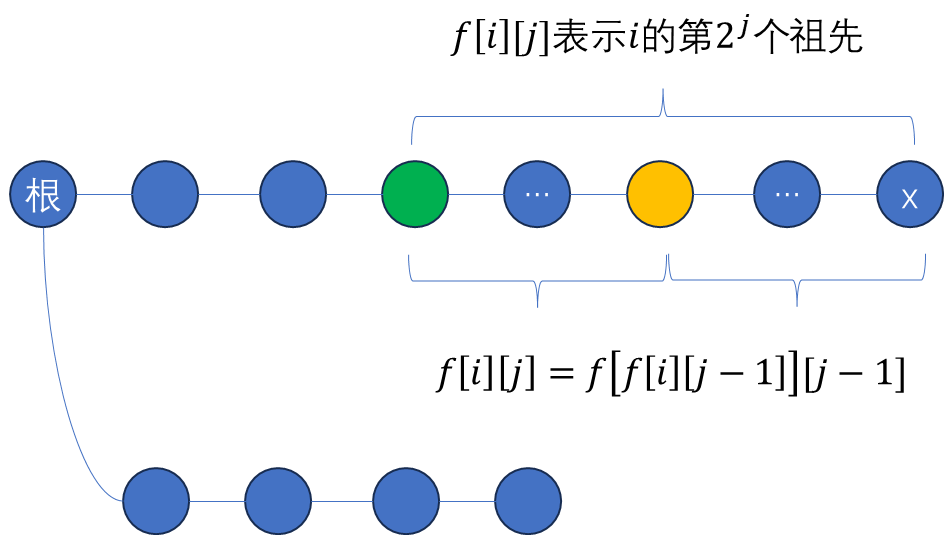
寻找$\text{LCA}(x,y)$过程可以分为两个阶段：

• 第一阶段中，将 $x,y$ 两点跳转到同一深度。
• 在第二阶段中，从最大的 $i$ 开始循环尝试，一直尝试到 $0$（包括 $0$），如果$f[x][i]\ne f[y][i]$，则 $x\leftarrow f[x][i],y\leftarrow f[y][i]$，那么最后的 LCA 为 $f[x][0]$（或$f[y][0]$）。

时间复杂度

• 倍增算法的预处理时间复杂度为$O(n\log n)$
• 单次查询时间复杂度为 $O(\log n)$

代码实现

#include <iostream>
#include <vector>
using namespace std;
const int N = 40010;
vector<int> g[N];
//f[i][j]表示从结点i的第2^j个祖先
int f[N][20], depth[N];
//预处理每个结点的深度和f[i][j]
void dfs(int i, int fa)
{
    depth[i] = depth[fa] + 1;
    f[i][0] = fa;
    //计算f[i][j]
    for(int j = 1; j <= 15; j ++) f[i][j] = f[f[i][j - 1]][j - 1];
    //递归计算i的子结点
    for(int j : g[i])
        if(j != fa) dfs(j, i);
}
int LCA(int x, int y)
{
    //将x设置为较深结点
    if(depth[x] < depth[y]) swap(x, y);
    //将x向上跳，直到跳到同一层
    for(int k = 15; k >= 0; k --)
        //如果f[u][j]跳出了根结点，由于depth[0]=0，跳转的条件不成立
        if(depth[f[x][k]] >= depth[y])
            x = f[x][k];
    //如果y恰好是公共祖先
    if(x == y) return x;
    //将x和y同时向上跳，直到跳到最近公共祖先的下一层
    for(int k = 15; k >= 0; k --)
    {
        //如果x和y都跳出了根结点，由于depth[0]=0，值同时为0，相等则不会跳转
        if(f[x][k] != f[y][k])
        {
            x = f[x][k], y = f[y][k];
        }
    }
    //注意：最后返回的是父结点
    return f[x][0];
}
int main()
{
    int n, m, root;
    cin >> n;
    for(int i = 0; i < n; i ++)
    {
        int a, b;
        cin >> a >> b;
        //邻接表保存树
        if(b != -1) g[a].push_back(b), g[b].push_back(a);
        else root = a;
    }
    //预处理每个结点的深度和f[i][j]
    dfs(root, 0);
    //处理询问
    cin >> m;
    while (m -- )
    {
        int x, y;
        cin >> x >> y;
        int lca = LCA(x, y);
        if(x == lca) puts("1");
        else if(y == lca) puts("2");
        else puts("0");
    }
}