DS|二叉树

news2024/11/20 20:25:04

题目一：DS二叉树 -- 二叉树构建与遍历

题目描述：

给定一颗二叉树的逻辑结构如下图，（先序遍历的结果，空树用字符‘#’表示，例如AB#C##D##），建立该二叉树的二叉链式存储结构，并输出该二叉树的先序遍历、中序遍历和后序遍历结果。

输入要求：

第一行输入一个整数t，表示有t个二叉树

第二行起输入每个二叉树的先序遍历结果，空树用字符‘#’表示，连续输入t行。

输出要求：

输出每个二叉树的先序遍历、中序遍历和后序遍历结果。

输入样例：

2
AB#C##D##
AB##C##

输出样例：

ABCD
BCAD
CBDA
ABC
BAC
BCA

代码示例：

#include <iostream>
#include <string>
#include <cstring>
#include <iomanip>
#include <algorithm>
#include <cmath>
using namespace std;

struct BNode {
	char data;
	BNode* lChild;
	BNode* rChild;
};

class BTree {
public:
	BNode* root;
	BTree() :root(NULL) {}
	BNode* creatBTree() {
		BNode* tmp;
		char ch;
		cin >> ch;
		if (ch == '#') tmp = NULL;
		else {
			tmp = new BNode;
			tmp->data = ch;
			tmp->lChild = creatBTree();
			tmp->rChild = creatBTree();
		}
		return tmp;
	}

	void Preorder(BNode* cur) {
		if (cur != NULL) {
			cout << cur->data;
			Preorder(cur->lChild), Preorder(cur->rChild);
		}
	}

	void Inorder(BNode* cur) {
		if (cur != NULL) {
			Inorder(cur->lChild);
			cout << cur->data;
			Inorder(cur->rChild);
		}
	}

	void Postorder(BNode* cur) {
		if (cur != NULL) {
			Postorder(cur->lChild), Postorder(cur->rChild);
			cout << cur->data;
		}
	}
};

int main() {
	int t;
	cin >> t;
	while (t--) {
		BTree tree;
		tree.root = tree.creatBTree();
		tree.Preorder(tree.root);
		cout << endl;
		tree.Inorder(tree.root);
		cout << endl;
		tree.Postorder(tree.root);
		cout << endl;
	}

}

题目二：DS二叉树 -- 叶子数量

题目描述：

计算一颗二叉树包含的叶子结点数量。

提示：叶子是指它的左右孩子为空。

建树方法采用“先序遍历+空树用0表示”的方法，即给定一颗二叉树的先序遍历的结果为AB0C00D00，其中空节点用字符‘0’表示。则该树的逻辑结构如下图。

输入要求：

第一行输入一个整数t，表示有t个测试数据

第二行起输入二叉树先序遍历的结果，空树用字符‘0’表示，输入t行

输出要求：

逐行输出每个二叉树的包含的叶子数量

输入样例：

3
AB0C00D00
AB00C00
ABC00D00E00

输出样例：

2
2
3

代码示例：

#include <iostream>
#include <string>
#include <cstring>
#include <iomanip>
#include <algorithm>
#include <cmath>
using namespace std;

struct BNode {
	char data;
	BNode* lChild;
	BNode* rChild;
};

class BTree {
public:
	BNode* root;
	BTree() :root(NULL) {}
	BNode* creatBTree() {
		BNode* tmp;
		char ch;
		cin >> ch;
		if (ch == '0') tmp = NULL;
		else {
			tmp = new BNode;
			tmp->data = ch;
			tmp->lChild = creatBTree();
			tmp->rChild = creatBTree();
		}
		return tmp;
	}

	void Preorder(BNode* cur) {
		if (cur != NULL) {
			cout << cur->data;
			Preorder(cur->lChild), Preorder(cur->rChild);
		}
	}

	void Inorder(BNode* cur) {
		if (cur != NULL) {
			Inorder(cur->lChild);
			cout << cur->data;
			Inorder(cur->rChild);
		}
	}

	void Postorder(BNode* cur) {
		if (cur != NULL) {
			Postorder(cur->lChild), Postorder(cur->rChild);
			cout << cur->data;
		}
	}

	void countLeaves(BNode* cur, int& count) {
		if (cur != NULL) {
			if (cur->lChild == NULL && cur->rChild == NULL) count++;
			countLeaves(cur->lChild, count), countLeaves(cur->rChild, count);
		}
	}
};

int main() {
	int t;
	cin >> t;
	while (t--) {
		int count = 0;
		BTree tree;
		tree.root = tree.creatBTree();
		tree.countLeaves(tree.root, count);
		cout << count << endl;
	}
	return 0;
}

题目三：DS二叉树 -- 父子结点

题目描述：

给定一颗二叉树的逻辑结构如下图，（先序遍历的结果，空树用字符‘0’表示，例如AB0C00D00），建立该二叉树的二叉链式存储结构。

编写程序输出该树的所有叶子结点和它们的父亲结点

输入要求：

第一行输入一个整数t，表示有t个二叉树

第二行起，按照题目表示的输入方法，输入每个二叉树的先序遍历，连续输入t行

输出要求：

第一行按先序遍历，输出第1个示例的叶子节点

第二行输出第1个示例中与叶子相对应的父亲节点

以此类推输出其它示例的结果

输入样例：

3
AB0C00D00
AB00C00
ABCD0000EF000

输出样例：

C D 
B A 
B C 
A A 
D F 
C E

代码示例：

#include <iostream>
#include <string>
#include <cstring>
#include <iomanip>
#include <algorithm>
#include <cmath>
using namespace std;

struct BNode {
	char data;
	BNode* lChild;
	BNode* rChild;
};

class BTree {
public:
	BNode* root;
	BTree() :root(NULL) {}
	BNode* creatBTree() {
		BNode* tmp;
		char ch;
		cin >> ch;
		if (ch == '0') tmp = NULL;
		else {
			tmp = new BNode;
			tmp->data = ch;
			tmp->lChild = creatBTree();
			tmp->rChild = creatBTree();
		}
		return tmp;
	}

	void Preorder(BNode* cur) {
		if (cur != NULL) {
			cout << cur->data;
			Preorder(cur->lChild), Preorder(cur->rChild);
		}
	}

	void Inorder(BNode* cur) {
		if (cur != NULL) {
			Inorder(cur->lChild);
			cout << cur->data;
			Inorder(cur->rChild);
		}
	}

	void Postorder(BNode* cur) {
		if (cur != NULL) {
			Postorder(cur->lChild), Postorder(cur->rChild);
			cout << cur->data;
		}
	}

	void countLeaves(BNode* cur, int& count) {
		if (cur != NULL) {
			if (cur->lChild == NULL && cur->rChild == NULL) count++;
			countLeaves(cur->lChild, count), countLeaves(cur->rChild, count);
		}
	}

	void printLeaves(BNode* cur) {
		if (cur != NULL) {
			if (cur->lChild == NULL && cur->rChild == NULL) cout << cur->data << " ";
			printLeaves(cur->lChild), printLeaves(cur->rChild);
		}
	}

	void printLeavesFather(BNode* cur) {
		if (cur != NULL) {
			if (cur->lChild != NULL && cur->lChild->lChild == NULL && cur->lChild->rChild == NULL) cout << cur->data << " ";
			printLeavesFather(cur->lChild);
			if (cur->rChild != NULL && cur->rChild->lChild == NULL && cur->rChild->rChild == NULL) cout << cur->data << " ";
			printLeavesFather(cur->rChild);
		}
	}
};

int main() {
	int t;
	cin >> t;
	while (t--) {
		BTree tree;
		tree.root = tree.creatBTree();
		tree.printLeaves(tree.root);
		cout << endl;
		tree.printLeavesFather(tree.root);
		cout << endl;
	}
	return 0;
}

题目四：DS二叉树 -- 层次遍历

题目描述：

层次遍历二叉树，是从根结点开始遍历，按层次次序“自上而下，从左至右”访问树中的各结点。

建树方法采用“先序遍历+空树用0表示”的方法

建议使用队列结构实现，算法框架如下：

定义一个空白队列和一个树结点指针p

设T是指向根结点的指针变量，若二叉树为空，则返回；否则，令p=T，p入队，执行以下循环：

(1)队首元素出队到p；

(2)访问p所指向的结点； 

(3)p所指向的结点的左、右子结点依次入队。

(4)跳转步骤1循环，直到队列空为止

例如把上述算法中的访问操作定义为输出，算法结果就是把二叉树按层次遍历输出

输入要求：

第一行输入一个整数t，表示有t个测试数据

第二行起输入二叉树先序遍历的结果，空树用字符‘0’表示，输入t行

输出要求：

逐行输出每个二叉树的层次遍历结果

输入样例：

2
AB0C00D00
ABCD00E000FG00H0I00

输出样例：

ABDC
ABFCGHDEI

代码示例：

#include <iostream>
#include <string>
#include <cstring>
#include <iomanip>
#include <algorithm>
#include <cmath>
#include <queue>
using namespace std;

struct BNode {
	char data;
	BNode* lChild;
	BNode* rChild;
};

class BTree {
public:
	BNode* root;
	BTree() :root(NULL) {}
	BNode* creatBTree() {
		BNode* tmp;
		char ch;
		cin >> ch;
		if (ch == '0') tmp = NULL;
		else {
			tmp = new BNode;
			tmp->data = ch;
			tmp->lChild = creatBTree();
			tmp->rChild = creatBTree();
		}
		return tmp;
	}

	void Preorder(BNode* cur) {
		if (cur != NULL) {
			cout << cur->data;
			Preorder(cur->lChild), Preorder(cur->rChild);
		}
	}

	void Inorder(BNode* cur) {
		if (cur != NULL) {
			Inorder(cur->lChild);
			cout << cur->data;
			Inorder(cur->rChild);
		}
	}

	void Postorder(BNode* cur) {
		if (cur != NULL) {
			Postorder(cur->lChild), Postorder(cur->rChild);
			cout << cur->data;
		}
	}

	void countLeaves(BNode* cur, int& count) {
		if (cur != NULL) {
			if (cur->lChild == NULL && cur->rChild == NULL) count++;
			countLeaves(cur->lChild, count), countLeaves(cur->rChild, count);
		}
	}

	void printLeaves(BNode* cur) {
		if (cur != NULL) {
			if (cur->lChild == NULL && cur->rChild == NULL) cout << cur->data << " ";
			printLeaves(cur->lChild), printLeaves(cur->rChild);
		}
	}

	void printLeavesFather(BNode* cur) {
		if (cur != NULL) {
			if (cur->lChild != NULL && cur->lChild->lChild == NULL && cur->lChild->rChild == NULL) cout << cur->data << " ";
			printLeavesFather(cur->lChild);
			if (cur->rChild != NULL && cur->rChild->lChild == NULL && cur->rChild->rChild == NULL) cout << cur->data << " ";
			printLeavesFather(cur->rChild);
		}
	}

	void levelDFSTree(BNode* cur) {
		queue<BNode*> Q;
		BNode* p = cur;
		if (p) Q.push(p);
		while (!Q.empty()) {
			p = Q.front();
			Q.pop();
			if (p) {
				cout << p->data;
				Q.push(p->lChild), Q.push(p->rChild);
			}
		}
		cout << endl;
	}
};

int main() {
	int t;
	cin >> t;
	while (t--) {
		BTree tree;
		tree.root = tree.creatBTree();
		tree.levelDFSTree(tree.root);
	}
	return 0;
}

题目五：DS二叉树 -- 二叉树高度

题目描述：

给出一棵二叉树，求它的高度。

注意，二叉树的层数是从1开始

输出要求：

第一行输入一个整数t，表示有t个二叉树

第二行起输入每个二叉树的先序遍历结果，空树用字符‘0’表示，连续输入t行

输出要求：

每行输出一个二叉树的高度

输入样例：

1
AB0C00D00

输出样例：

3

代码示例：

#include <iostream>
#include <string>
#include <cstring>
#include <iomanip>
#include <algorithm>
#include <cmath>
#include <queue>
using namespace std;

struct BNode {
	char data;
	BNode* lChild;
	BNode* rChild;
};

class BTree {
public:
	BNode* root;
	BTree() :root(NULL) {}
	BNode* creatBTree() {
		BNode* tmp;
		char ch;
		cin >> ch;
		if (ch == '0') tmp = NULL;
		else {
			tmp = new BNode;
			tmp->data = ch;
			tmp->lChild = creatBTree();
			tmp->rChild = creatBTree();
		}
		return tmp;
	}

	void Preorder(BNode* cur) {
		if (cur != NULL) {
			cout << cur->data;
			Preorder(cur->lChild), Preorder(cur->rChild);
		}
	}

	void Inorder(BNode* cur) {
		if (cur != NULL) {
			Inorder(cur->lChild);
			cout << cur->data;
			Inorder(cur->rChild);
		}
	}

	void Postorder(BNode* cur) {
		if (cur != NULL) {
			Postorder(cur->lChild), Postorder(cur->rChild);
			cout << cur->data;
		}
	}

	void countLeaves(BNode* cur, int& count) {
		if (cur != NULL) {
			if (cur->lChild == NULL && cur->rChild == NULL) count++;
			countLeaves(cur->lChild, count), countLeaves(cur->rChild, count);
		}
	}

	void printLeaves(BNode* cur) {
		if (cur != NULL) {
			if (cur->lChild == NULL && cur->rChild == NULL) cout << cur->data << " ";
			printLeaves(cur->lChild), printLeaves(cur->rChild);
		}
	}

	void printLeavesFather(BNode* cur) {
		if (cur != NULL) {
			if (cur->lChild != NULL && cur->lChild->lChild == NULL && cur->lChild->rChild == NULL) cout << cur->data << " ";
			printLeavesFather(cur->lChild);
			if (cur->rChild != NULL && cur->rChild->lChild == NULL && cur->rChild->rChild == NULL) cout << cur->data << " ";
			printLeavesFather(cur->rChild);
		}
	}

	void levelDFSTree(BNode* cur) {
		queue<BNode*> Q;
		BNode* p = cur;
		if (p) Q.push(p);
		while (!Q.empty()) {
			p = Q.front();
			Q.pop();
			if (p) {
				cout << p->data;
				Q.push(p->lChild), Q.push(p->rChild);
			}
		}
		cout << endl;
	}

	int TreeHeight(BNode* cur) {
		if (cur == NULL) return 0;
		else return max(TreeHeight(cur->lChild), TreeHeight(cur->rChild)) + 1;
	}
};

int main() {
	int t;
	cin >> t;
	while (t--) {
		BTree tree;
		tree.root = tree.creatBTree();
		cout << tree.TreeHeight(tree.root) << endl;
	}
	return 0;
}

题目六：DS二叉树 -- 二叉树之数组存储

题目描述：

二叉树可以采用数组的方法进行存储，把数组中的数据依次自上而下,自左至右存储到二叉树结点中，一般二叉树与完全二叉树对比，比完全二叉树缺少的结点就在数组中用0来表示。如下图所示

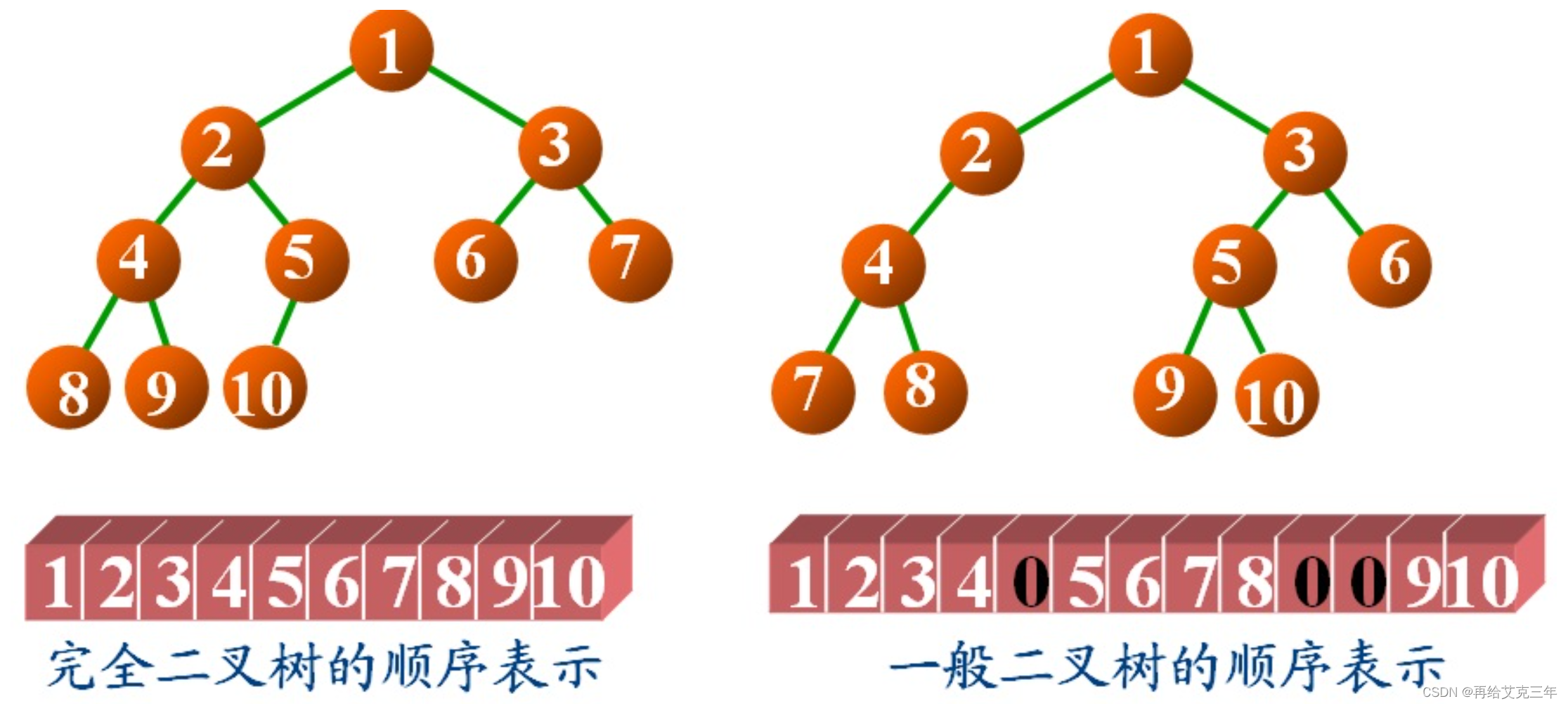
从上图可以看出，右边的是一颗普通的二叉树，当它与左边的完全二叉树对比，发现它比完全二叉树少了第5号结点，所以在数组中用0表示，同样它还少了完全二叉树中的第10、11号结点，所以在数组中也用0表示。

结点存储的数据均为非负整数

输入要求：

第一行输入一个整数t，表示有t个二叉树

第二行起，每行输入一个数组，先输入数组长度，再输入数组内数据，每个数据之间用空格隔开，输入的数据都是非负整数

连续输入t行

输出要求：

每行输出一个示例的先序遍历结果，每个结点之间用空格隔开

输入样例：

3
3 1 2 3
5 1 2 3 0 4
13 1 2 3 4 0 5 6 7 8 0 0 9 10

输出样例：

1 2 3 
1 2 4 3 
1 2 4 7 8 3 5 9 10 6

代码示例：

#include <iostream>
#include <string>
#include <cstring>
#include <iomanip>
#include <algorithm>
#include <cmath>
#include <queue>
using namespace std;

class BTNode {
public:
	int data;
	BTNode* lChild;
	BTNode* rChild;
	BTNode() :lChild(NULL), rChild(NULL) {}
};

class BTree {
public:
	BTNode* root;
	BTree() :root(NULL) {}
	~BTree() { DeleteTree(); }
	BTNode* creatBTree() {
		BTNode* tmp;
		int ch;
		cin >> ch;
		if (ch == 0) tmp = NULL;
		else {
			tmp = new BTNode;
			tmp->data = ch;
			tmp->lChild = creatBTree();
			tmp->rChild = creatBTree();
		}
		return tmp;
	}
	BTNode* creatBTree(queue<int> qint) {
		BTNode* tmp = new BTNode;
		BTNode* empty = new BTNode;
		BTNode bridge;
		queue<BTNode*> qnode;
		if (!qint.front()) return NULL;
		tmp->data = qint.front();
		qint.pop();
		qnode.push(tmp);
		while (!qint.empty()) {
			if (qint.front() == 0) {
				qnode.front()->lChild = NULL;
				qnode.push(empty);
			}
			else {
				qnode.front()->lChild = new BTNode;
				qnode.front()->lChild->data = qint.front();
				qnode.push(qnode.front()->lChild);
			}
			qint.pop();

			if (qint.front() == 0) {
				qnode.front()->rChild = NULL;
				qnode.push(empty);
			}
			else {
				qnode.front()->rChild = new BTNode;
				qnode.front()->rChild->data = qint.front();
				qnode.push(qnode.front()->rChild);
			}
			qint.pop();

			qnode.pop();
		}

		return tmp;
	}
	void Destory(BTNode* cur) {
		if (cur != NULL) {
			Destory(cur->lChild), Destory(cur->rChild);
			delete cur;
		}
	}
	void DeleteTree() { Destory(root); root = NULL; }

	void Preorder(BTNode* cur) {
		if (cur != NULL) {
			cout << cur->data << " ";
			Preorder(cur->lChild), Preorder(cur->rChild);
		}
	}

	void Inorder(BTNode* cur) {
		if (cur != NULL) {
			Inorder(cur->lChild);
			cout << cur->data;
			Inorder(cur->rChild);
		}
	}

	void Postorder(BTNode* cur) {
		if (cur != NULL) {
			Postorder(cur->lChild), Postorder(cur->rChild);
			cout << cur->data;
		}
	}

	void Countleaves(BTNode* cur, int& count) {
		if (cur != NULL) {
			if (cur->lChild == NULL && cur->rChild == NULL) count++;
			Countleaves(cur->lChild, count), Countleaves(cur->rChild, count);
		}
	}

	void Printleaves(BTNode* cur) {
		if (cur != NULL) {
			if (cur->lChild == NULL && cur->rChild == NULL) cout << cur->data << " ";
			Printleaves(cur->lChild), Printleaves(cur->rChild);
		}
	}

	void PrintleavesFather(BTNode* cur) {
		if (cur != NULL) {
			if (cur->lChild != NULL && cur->lChild->lChild == NULL && cur->lChild->rChild == NULL) cout << cur->data << " ";
			PrintleavesFather(cur->lChild), PrintleavesFather(cur->rChild);
			if (cur->rChild != NULL && cur->rChild->lChild == NULL && cur->rChild->rChild == NULL) cout << cur->data << " ";
		}
	}

	void levelDFSTree(BTNode* cur) {
		queue<BTNode*> Q;
		BTNode* p = cur;
		if (p) Q.push(p);
		while (!Q.empty()) {
			p = Q.front();
			Q.pop();
			if (p) {
				cout << p->data;
				Q.push(p->lChild), Q.push(p->rChild);
			}
		}
		cout << endl;
	}

	int TreeHeight(BTNode* cur) {
		if (cur == NULL) return 0;
		else return max(TreeHeight(cur->lChild), TreeHeight(cur->rChild)) + 1;
	}
};


int main() {
	int t;
	cin >> t;
	while (t--) {
		queue<int> que;
		int n;
		cin >> n;
		while (n--) {
			int number;
			cin >> number;
			que.push(number);
		}
		BTree tree;
		tree.root = tree.creatBTree(que);
		tree.Preorder(tree.root);
		cout << endl;
	}
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1358275.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【React系列】JSX核心语法和原理

【React系列】JSX核心语法和原理

本文来自#React系列教程&#xff1a;https://mp.weixin.qq.com/mp/appmsgalbum?__bizMzg5MDAzNzkwNA&actiongetalbum&album_id1566025152667107329) 一. ES6 的 class 虽然目前React开发模式中更加流行hooks&#xff0c;但是依然有很多的项目依然是使用类组件&#x…
阅读更多...
李沐机器学习系列5---循环神经网络

李沐机器学习系列5---循环神经网络

1 Introduction 对于样本的分析&#xff0c;通过全连接层处理表格数据&#xff0c;通过卷积神经网络处理图像数据&#xff1b;第一种假设&#xff0c;所有数据都是独立同分布的RNN 处理序列信号 序列数据的更多场景 1&#xff09;用户使用习惯具有时间的先后性 2&#xff09;外…
阅读更多...
【Vm】兆懿，安卓虚拟机

【Vm】兆懿，安卓虚拟机

以前用了Win11安卓子系统&#xff0c;体验不好 这次试试兆懿。弄了几个小时&#xff0c;终于安装成功 实际体验极差&#xff1a;虚拟机占用内存多机箱一直呜呜叫个不停&#xff1b;打开软件发现卡到爆炸还时不时闪退 为了不让他占空间&#xff0c;第二天卸载。 虚拟机就是折腾着…
阅读更多...
java实现list去重（四种方法）

java实现list去重（四种方法）

&#x1f4d1;前言 本文主要是【Java】——java实现list去重&#xff08;四种方法&#xff09;的文章&#xff0c;如果有什么需要改进的地方还请大佬指出⛺️ &#x1f3ac;作者简介&#xff1a;大家好&#xff0c;我是听风与他&#x1f947; ☁️博客首页&#xff1a;CSDN主页…
阅读更多...
工厂如何确定设备故障的原因？

工厂如何确定设备故障的原因？

设备故障是制造业中常见的问题&#xff0c;对生产效率和运营成本产生重大影响。为了解决设备故障并提高生产效率&#xff0c;确定设备故障的准确原因至关重要。本文将介绍一些关键步骤和方法&#xff0c;帮助工厂确定设备故障的原因。 1. 收集和分析数据 要确定设备故障的原因…
阅读更多...
互联网加竞赛 基于CNN实现谣言检测 - python 深度学习 机器学习

互联网加竞赛 基于CNN实现谣言检测 - python 深度学习 机器学习

文章目录 1 前言1.1 背景 2 数据集3 实现过程4 CNN网络实现5 模型训练部分6 模型评估7 预测结果8 最后 1 前言 &#x1f525; 优质竞赛项目系列&#xff0c;今天要分享的是 基于CNN实现谣言检测 该项目较为新颖&#xff0c;适合作为竞赛课题方向&#xff0c;学长非常推荐&am…
阅读更多...
局域网共享打印机设置

局域网共享打印机设置

一 配置共享打印机环境 方法1&#xff08;打印机连接的电有设置密码的设置&#xff09;&#xff1a; 1 需要在非直接连接打印机的pc上设置&#xff0c;登录账号&#xff0c;在控制面板中进入凭证管理&#xff0c;添加连接打印机主机的登录凭证 方法2&#xff08;免账号密码…
阅读更多...
【InnoDB数据存储结构】第3章节：区、段、碎片区和表空间

【InnoDB数据存储结构】第3章节：区、段、碎片区和表空间

文章目录结构 区、段、碎片区和表空间 什么是区&#xff1f;什么是段&#xff1f;什么是碎片区&#xff1f;什么是表空间&#xff1f; 在上文 InooDB 存储行格式一文中已经大致讲述过&#xff0c;再来回顾一下&#xff0c;直接上图&#xff1a; 名词解释如下&#xff1a; 行…
阅读更多...
使用 Parallels Desktop 彻底改变您的开发和测试工作流程

使用 Parallels Desktop 彻底改变您的开发和测试工作流程

Parallels Desktop 等虚拟机平台已经改变了应用程序开发和测试。 在当今快节奏的技术环境中&#xff0c;开发人员和测试人员现在能够在虚拟沙箱中进行操作&#xff0c;能够使用容器、虚拟机或 Kubernetes 集群快速创建和拆除类似虚拟生产的环境。 无论您是为 Windows 或 Mac …
阅读更多...
（03）光刻——半导体电路的绘制

（03）光刻——半导体电路的绘制

01、绘制精细电路的第一步 金属-氧化物半导体场效应晶体管（MOSFET）的革命，让我们可以在相同面积的晶圆上同时制造出更多晶体管。MOSFET体积越小，单个 MOSFET的耗电量就越少，还可以制造出更多的晶体管，让其发挥作用，可谓是一举多得。可见，制造更小的MOSFET成了关键因素…
阅读更多...
第五周：深度学习知识点回顾

第五周：深度学习知识点回顾

前言&#xff1a; 讲真&#xff0c;复习这块我是比较头大的&#xff0c;之前的线代、高数、概率论、西瓜书、樱花书、NG的系列课程、李宏毅李沐等等等等…那可是花了三年学习佳实践下来的&#xff0c;现在一想脑子里就剩下几个名词就觉得废柴一个了&#xff0c;朋友们有没有同感…
阅读更多...
SDRAM小项目——SDRAM初始化配置

SDRAM小项目——SDRAM初始化配置

主要写了SDRAM的初始化模块&#xff0c;注重文档信息的查找&#xff0c;时序图的设计&#xff0c;SDRAM仿真插件的使用。 文档信息&#xff1a; 根据文档说明&#xff0c;SDRAM在使用之前必须先进行初始化 初始化之前要进行100us的延迟&#xff0c;在100us内除了INHIBIT和NOP命…
阅读更多...
【数据分析实战】冰雪大世界携程景区评价信息情感分析采集词云

【数据分析实战】冰雪大世界携程景区评价信息情感分析采集词云

文章目录 引言数据采集数据集展示数据预处理 数据分析评价总体情况分析本人浅薄分析 各游客人群占比分析本人浅薄分析 各评分雷达图本人浅薄分析 差评词云-可视化本人浅薄分析 好评词云-可视化本人浅薄分析 综合分析写在最后 今年冬天&#xff0c;哈尔滨冰雪旅游"杀疯了&q…
阅读更多...
炫酷的倒计时引导页

炫酷的倒计时引导页

文章目录 文件分布介绍效果预览代码css样式Locationplayer.css js样式player.js 文件分布介绍 效果预览 代码 css样式 Location html {height: 100%;}body {font-family: "Helvetica Neue", "Luxi Sans", "DejaVu Sans", Tahoma, "Hirag…
阅读更多...
SwiftUI 打造一款收缩自如的 HStack（三）：“魔镜魔镜，我爱你”

SwiftUI 打造一款收缩自如的 HStack（三）：“魔镜魔镜，我爱你”

概览 在前两篇博文中，我们分别讨论了用 HStack 和 对齐+ZStack 来实现收缩自如“HStack”的方法。 虽然看起来“各有千秋”，但实际上它们都拖着一坨厚重的 datas，这不禁为其“减分不少”。 而从上图演示中可以看到：我们完全摆脱了 datas 数据的桎梏，现在我们可以按照轻松…
阅读更多...
【Java EE初阶九】多线程案例（线程池）

【Java EE初阶九】多线程案例（线程池）

一、线程池的引入 引入池---->主要是为了提高效率&#xff1b; 最开始&#xff0c;进程可以解决并发编程的问题&#xff0c;但是代价有点大了&#xff0c;于是引入了 “轻量级进程” ---->线程 线程也能解决并发编程的问题&#xff0c;而且线程的开销比进程要小的多&…
阅读更多...
JS新手入门笔记整理：条件判断

JS新手入门笔记整理：条件判断

判断语句&#xff1a;IF 单向判断&#xff1a;if... 语法 if&#xff08;条件&#xff09; {…… } 如果“条件”返回结果为true&#xff0c;则会执行大括号{}内部的程序&#xff1b;如果“条件”返回结果为false&#xff0c;则会直接跳过大括号{}内部的程序&#xff0c;然后…
阅读更多...
Python中User-Agent的重要作用及实际应用

Python中User-Agent的重要作用及实际应用

摘要&#xff1a; User-Agent是HTTP协议中的一个重要字段&#xff0c;用于标识发送请求的客户端信息。在Python中&#xff0c;User-Agent的作用至关重要&#xff0c;它可以影响网络请求的结果和服务器端的响应。将介绍User-Agent在Python中的重要作用&#xff0c;并结合实际案…
阅读更多...
编码器原理详解

编码器原理详解

编码器 什么是编码器 编码器可以用来将信息编码成为二进制代码&#xff0c;有点类似于取代号&#xff0c;人为的将二进制代码与对应的信息联系起来。 如下图所示&#xff1a; 假设有这三种情况会发生&#xff0c;且每次只发生一种情况 为了给这三种情况做一个区分&#xff…
阅读更多...
FPGA - 240102 - FPGA期末速成

FPGA - 240102 - FPGA期末速成

TAG - F P G A 、期末、速成 FPGA、期末、速成 FPGA、期末、速成 // – 习题1 – //CPLD&#xff08;Complex Programmable Logic Device&#xff09;是 Complex PLD 的简称&#xff0c;一种较 PLD 为复杂的逻辑元件。CPLD 逻辑资源多寄存器少&#xff0c;FPGA 逻辑弱而寄存器…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023