目录
题目
思路
解题方法
题目
https://leetcode.cn/problems/maximum-rows-covered-by-columns/description/
给你一个下标从 0 开始、大小为 m x n 的二进制矩阵 matrix ;另给你一个整数 numSelect,表示你必须从 matrix 中选择的 不同 列的数量。
如果一行中所有的 1 都被你选中的列所覆盖,则认为这一行被 覆盖 了。
形式上,假设 s = {c1, c2, ...., cnumSelect} 是你选择的列的集合。对于矩阵中的某一行 row ,如果满足下述条件,则认为这一行被集合 s 覆盖:
- 对于满足
matrix[row][col] == 1的每个单元格matrix[row][col](0 <= col <= n - 1),col均存在于s中,或者 row中 不存在 值为1的单元格。
你需要从矩阵中选出 numSelect 个列,使集合覆盖的行数最大化。
返回一个整数,表示可以由 numSelect 列构成的集合 覆盖 的 最大行数 。
示例 1:
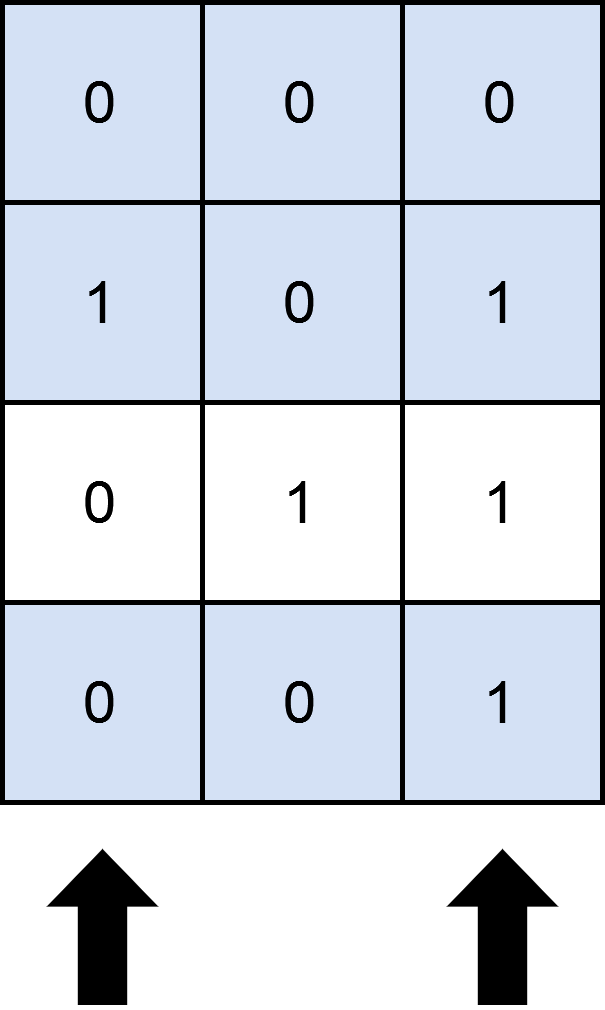
输入:matrix = [[0,0,0],[1,0,1],[0,1,1],[0,0,1]], numSelect = 2
输出:3
解释:
图示中显示了一种覆盖 3 行的可行办法。
选择 s = {0, 2} 。
- 第 0 行被覆盖,因为其中没有出现 1 。
- 第 1 行被覆盖,因为值为 1 的两列(即 0 和 2)均存在于 s 中。
- 第 2 行未被覆盖,因为 matrix[2][1] == 1 但是 1 未存在于 s 中。
- 第 3 行被覆盖,因为 matrix[2][2] == 1 且 2 存在于 s 中。
因此,可以覆盖 3 行。
另外 s = {1, 2} 也可以覆盖 3 行,但可以证明无法覆盖更多行。
示例 2:

输入:matrix = [[1],[0]], numSelect = 1 输出:2 解释: 选择唯一的一列,两行都被覆盖了,因为整个矩阵都被覆盖了。 所以我们返回 2 。
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 12matrix[i][j]要么是0要么是11 <= numSelect <= n
思路
我们观察一下数据,n<=12,所以我们可以遍历所有的列的组合,再判断此时有多少行被覆盖,保留被覆盖的最多的那一组数
解题方法
我们在编写代码过程中,使用了二进制保存状态,row数组记录每一行的二进制,但需要注意的是,我们记录的是这一行对应的二进制数的对称的那个数,比如,011,我们记录为110,即6,因为我们最终只要统计出现的最大次数,所以记录形式并不影响最终结果
class Solution {
public int maximumRows(int[][] matrix, int numSelect) {
int m = matrix.length,n=matrix[0].length;
int[] row = new int[m];
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
row[i] |= matrix[i][j]<<j;
}
}
int cnt = 0;
for(int i=0;i<(1<<n);i++){
if(Integer.bitCount(i) == numSelect){
int currentRows = 0;
for(int j=0;j<m;j++){
if((row[j] & i) == row[j]) {
currentRows+=1;
}
cnt = Math.max(currentRows,cnt);
}
}
}
return cnt;
}
}