正定矩阵在格密码中的应用（知识铺垫）

news2024/11/29 5:51:25

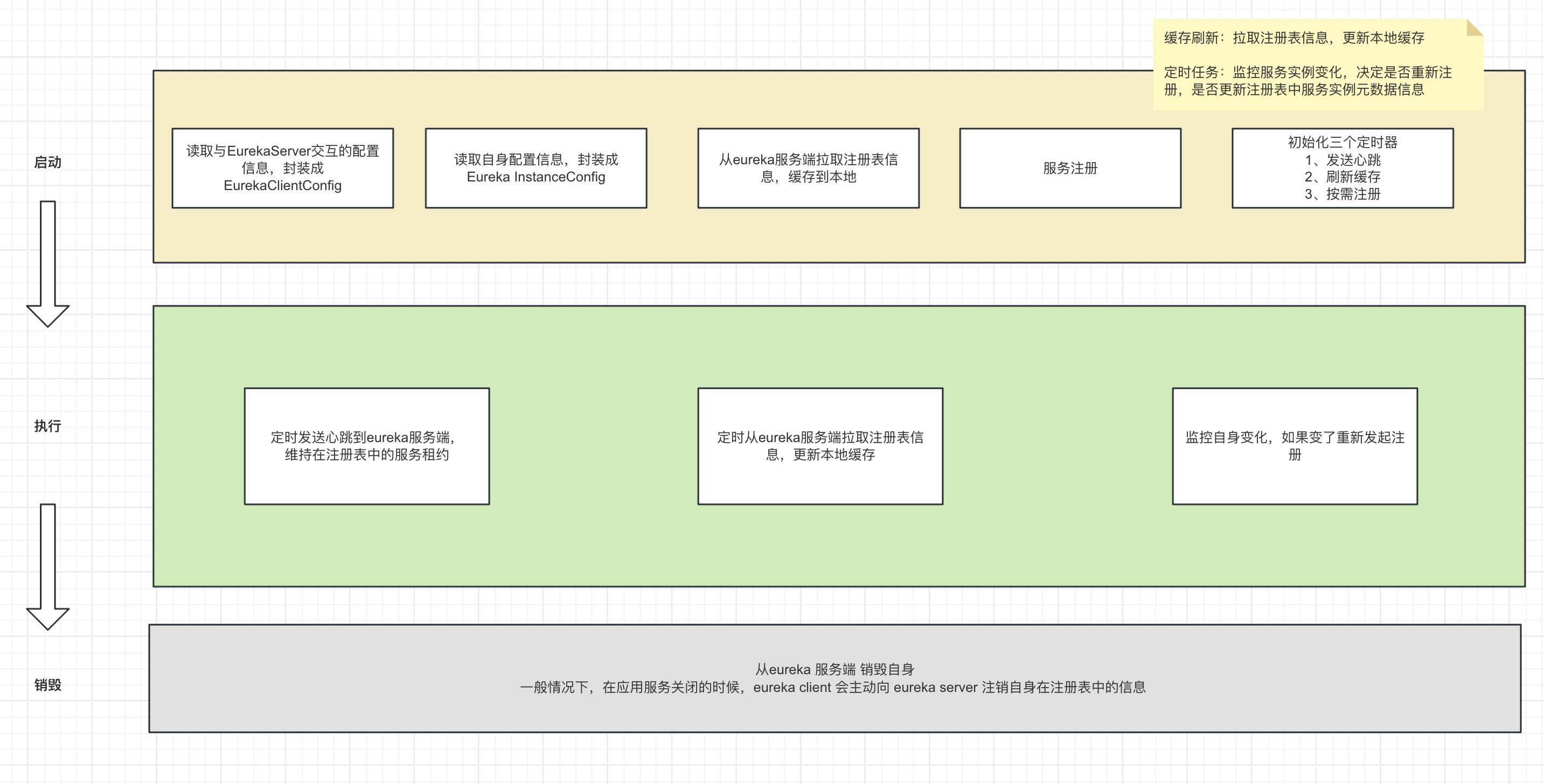
一. 写在前面

二. 最小值点

三. 二次型结构

四. 正定与非正定讨论

4.1 对参数a的要求

4.2 对参数c的要求

4.3 对参数b的要求

五. 最小值，最大值与奇异值

5.1 正定型（positive definite）

5.2 负定型（negative definite）

5.3 奇异型

六. 鞍点（saddle point）

七. 矩阵二次型

7.1 介绍

7.2 举例

例题1

例题2

例题3

八. 正定矩阵与格密码

一. 写在前面

格密码中有时要求格基矩阵是正定的，本文章将从方程和矩阵角度来解释正定性，辅助格密码的理解。

推荐可以先看下这篇文章：

格密码与线性代数-CSDN博客

对称矩阵一定有实数特征值（real eigenvalue）,本文章尝试在不计算矩阵特征值的情况下，快速判断矩阵特征值是否全为正数，其中涉及三个矩阵的基本概念：矩阵的主元（pivot），行列式，特征值。

二. 最小值点

在微分方程中，如果特征值为负数，那么以下函数单调递减：

$e^{\lambda t}$

在密码学或计算机领域的优化问题（optimization）经常需要判断N维情况下的最小值，数学知识告诉我们这与二阶导（second derivative test）相关，举两个例子：

尝试求这两个二维函数 $F(x,y),f(x,y)$ 的最小值。

首先可计算：

$F(0,0)=7,\quad f(0,0)=0$

很明显，最小值肯定要求一阶导数为0，也就是所谓的关注linear term，发现（0,0）该点符合要求，如下：

也就是（0,0）为这两个函数的极值点（stationary point）。

第一个平面z=F(x,y)与水平面z=7相切；

第二个平面z=f(x,y)与水平面z=0相切；

一阶导分析完毕来看下在（0,0）位置的二阶导，如下：

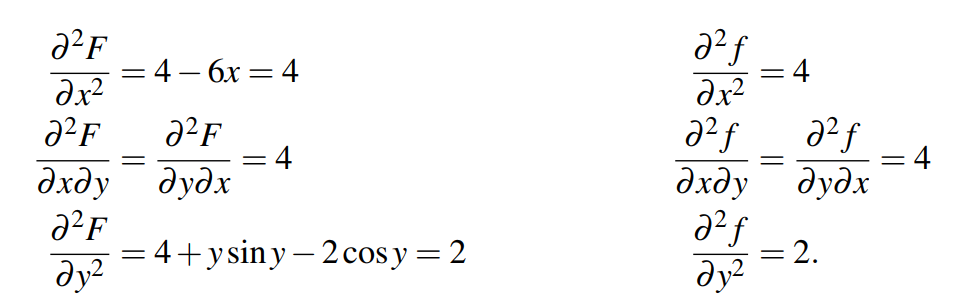
这两个二维函数的二阶导值一样，说明两个函数的性质相同。实际上F(x,y)的最高次幂为 $-x^3$ ，所以其最小值为 $-\infty$ ，接下来我们把重心放在f(x,y)。

三. 二次型结构

以上讨论中f(x,y）的形式为二次型：

$f=ax^2+2bxy+cy^2$

易得在（0,0）处，该类函数的一阶微分：

$\frac{\partial f}{\partial x}=\frac{\partial f}{\partial y}=0$

也就是该类二次型，原点一定是其极值点。

如果极小值点（local minimum）也是最小值点（global minimum），那么可得此类平面的图形像一个碗，碗的底部就是原点，如下图：

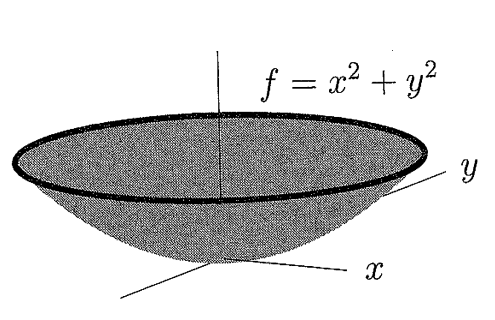
如果极值点不在原点处，而在其他任意点处，比如在 $x=\alpha,y=\beta$ ，其二阶导如下：

除了原点外，如果函数严格为正数，那么称之为正定（positive definite）。

四. 正定与非正定讨论

对于单变量的函数来讲，二阶大于0，函数拥有最小值，如下：

$\frac{\partial^2 F}{\partial x^2}>0$

反之，则函数有最大值。

对于二维函数来讲，函数拥有三个二阶导函数：

$F_{xx}\quad F_{xy}=F_{yx}\quad F_{yy}$

期待利用这三个数来判断函数拥有最小值还是最大值。

目标：什么情况下，二次型 $f(x,y)=ax^2+2bxy+cy^2$ 为正定的？

4.1 对参数a的要求

当x=1,y=0时，可得：

$ax^2+2bxy+cy^2=a$

正定性要求a为正数，利用导数的观点解释则是：

$\frac{\partial^2 F}{\partial x^2}>0$

也就是该曲面沿着x轴向上弯曲。

4.2 对参数c的要求

当x=0时，沿着y轴方向可得：

$f(0,y)=cy^2$

很明显正定性要求c>0

举两个简单例子，大家可以快速判断下：

例1

$f(x,y)=x^2-10xy+y^2$

例2

$f(x,y)=2x^2+4xy+y^2$

解：

例1非正定，因为 $f(1,1)=-8$

例2非正定，因为 $f(1,-1)=-1$

4.3 对参数b的要求

将二次型结构转变为如下完全平方差形式：

观察右边第二项，要想函数正定，则必须：

$c-\frac{b^2}{a}>0$

也就是：

$ac>b^2$

五. 最小值，最大值与奇异值

5.1 正定型（positive definite）

根据以上讨论，要想二次型 $ax^2+2bxy+cy^2$ 为正定，需要满足：

$a>0,ac>b^2$

如果要求某点处的最小值，那么：

$\frac{\partial f}{\partial x}=\frac{\partial f}{\partial y}=0$

并且要求：

$\frac{\partial^2 F}{\partial x^2}>0\quad [\frac{\partial^2 F}{\partial x^2}][\frac{\partial^2 F}{\partial y^2}]>[\frac{\partial^2 F}{\partial x\partial y}]$

5.2 负定型（negative definite）

负定型的要求与正定型刚好相反，如下：

$a<0,ac>b^2$

由此可求该函数的最大值

5.3 奇异型

当a,b,c满足：

$ac=b^2$

易得当a>0时，该函数为半正定（positive semi-definite）

当a<0时，该函数为半负定（negative semi-definite）

也就是当x=b,y=-a时，该函数可以取0。原始的平面z=f(x,y)像一个碗，奇异情况下像一个山谷，举例：

$f=(x+y)^2$

六. 鞍点（saddle point）

鞍点要求：

$ac<b^2$

举例两个函数：

来看一个图像：

这种二次型既可以取正数，也可以取负数，所以为非定型（indifinite）。从图形上看，此时的极值点既不是最小值，也不是最大值，该点则被称之为鞍点（saddle point）。

七. 矩阵二次型

7.1 介绍

总结以上我们发现，二阶导数其实可以形成一个对称矩阵。将 $ax^2$ 和 $cy^2$ 放在对角线，将2bxy分成一半，放在剩下的两个位置上，由此二次型函数f(x,y)即可以表示成一个2行2列的矩阵，如下：

将此处的2维扩展到n维，便可以从矩阵的角度来理解函数的最大值与最小值。假定有n个变量 $x_1,\cdots,x_n$ ，将其写成列向量x的形式，那么对任意对称矩阵A，矩阵向量相乘与二次型之间是互相等效的，如下：

$x^TAx\quad f(x_1,\cdots,x_n)$

更具体来讲，如下：

对角线的元素 $a_{11}\sim a_{nn}$ 与 $x_1^2\sim x_n^2$ 相乘。对称形式 $a_{ij}=a_{ji}$ 合并后再相乘可得 $2a_{ij}x_ix_j$ ，即可以还原函数为：

$f=a_{11}x_1^2+2a_{12}x_1x_2+\cdots+a_{nn}x_n^2$

注意每一项都是二次型，当 $x=(0,0,\cdots,0)$ 时，函数的一阶导函数一定为0.该函数的切面是水平的，也就是其极值点。、

借助此理论即可判断当向量x为0时，函数 $f=x^TAx$ 存在最大值，最小值，还是鞍点。

7.2 举例

例题1

函数 $f=2x^2+4xy+y^2$ ，其对应矩阵如下：

$A=\begin{bmatrix} 2 &2 \\ 2& 1 \end{bmatrix}$

很明显为鞍点

例题2

函数f=2xy，其对应矩阵：

$A=\begin{bmatrix} 0 &1 \\1& 0 \end{bmatrix}$

很明显鞍点

例题3

给定函数如下：

$f=2x_1^2-2x_1x_2+2x_2^2-2x_2x_3+2x_3^2$

该函数拥有最小值，写成矩阵格式如下：

其实矩阵A可以看成二阶导的矩阵，也就是满足：

$a_{ij}=\frac{\partial^2 F}{\partial x_i\partial x_j}$

同理可得：

$a_{ji}=\frac{\partial^2 F}{\partial x_j\partial x_i}$

从这个角度也可以理解矩阵A为对称矩阵，很明显当原函数存在最小值时，矩阵A则为正定的。

八. 正定矩阵与格密码

正定矩阵与特征值有关，格基特征值的大小会影响格密码中光滑参数的大小，从而影响安全性。具体这方面的知识会陆续更新。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1356559.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！