参考链接：OpenVINS https://docs.openvins.com/index.html

---

1. Getting Started

  欢迎来到OpenVIINS项目！以下指南将帮助新用户下载软件并在我们支持的数据集上运行。此外，我们还提供有关如何在我们的系统上运行您自己的传感器的信息，并提供有关我们如何标定的指南。如果您发现任何缺失或需要澄清的地方，请随时提出问题。

High-level overview
  从高层次来看，该系统建立在几个关键算法之上我们以 ov_core 为核心，其中包含许多任何人都可以使用的标准计算机视觉算法和实用程序。具体来说，它存储以下大型组件：

• 稀疏特征视觉跟踪（基于 KLT 和描述符）
• 用于表示状态的基本数学类型
• 初始化过程
• 生成合成测量值的多传感器模拟器

  这个 ov_core 库由包含我们基于过滤器的估计器的 ov_msckf 系统使用。其中我们有状态、管理器、类型系统、预测和更新算法。我们鼓励用户查看特定文档，详细了解我们提供的内容。ov_eval 库有一堆评估方法和脚本，可以用来生成研究成果以供发表。

1.5 传感器标定 — 如何标定您自己的视觉惯性传感器

视觉惯性传感器
  有人可能会问为什么要使用视觉惯性传感器？主要原因是因为两种不同传感方式的互补性。摄像头提供高密度的环境外部测量，而IMU测量传感器平台的内部自我运动。IMU对于为估算器提供鲁棒性至关重要，同时在单眼摄像头的情况下还提供系统尺度。
  但是，在估计中利用IMU时存在一些挑战。IMU 需要估计其他偏置项，并且需要在相机和 IMU 之间进行高精度标定。此外，传感器之间相对时间戳中的小误差也会在动态轨迹中非常迅速地降低性能。在这个 OpenVINS 项目中，我们通过倡导在线估计相机和IMU之间的这些外参和时间偏移参数来解决这些问题。

相机内参标定（离线）
  第一个任务是校准相机内参，例如焦距、相机中心和畸变参数。我们的团队经常使用 Kalibr 校准工具箱进行内参和外参离线标定，方法是执行以下步骤：

1. 下载并构建 Kalibr 工具箱。
2. 打印出要使用的标定板（我们通常使用 Aprilgrid 6x6 0.8x0.8米）。
3. 确保传感器驱动程序使用正确的时间戳发布到 ROS 上。
4. 传感器准备。
   ● 通过减少曝光时间来限制运动模糊;
   ● 以低帧率发布，以允许数据集中较大的差异 （2-5hz）;
   ● 确保可以在图像中看到标定板;
   ● 确保您的传感器对焦（可以使用其 kalibr_camera_focus 或手动）
5. 录制 ROS 数据包，并确保可以从图像平面的不同方向，距离和每个部分看到标定板。您可以移动标定板并保持相机静止，也可以移动相机并保持标定板静止。
6. 最后运行校准。
   ● 将 kalibr_calibrate_cameras 与指定的话题一起使用
   ● 根据畸变程度，对鱼眼使用 pinhole-equi，或者如果畸变较低，则使用 pinhole-radtan
7. 检查最终结果，密切关注最终重投影误差图，良好的标定小于<0.2-0.5像素重投影误差。

IMU Intrinsic Calibration (Offline)
  另一个内参标定是计算惯性传感器固有噪声特性，这是批量优化所必需的，以将相机校准为IMU变换和任何VINS估计器，以便我们可以正确地概率融合图像和惯性读数。不幸的是，没有成熟的开源工具箱来查找这些值，而可以尝试我们的kalibr_allan项目，尽管该项目没有优化。具体来说，我们估计了以下噪声参数：

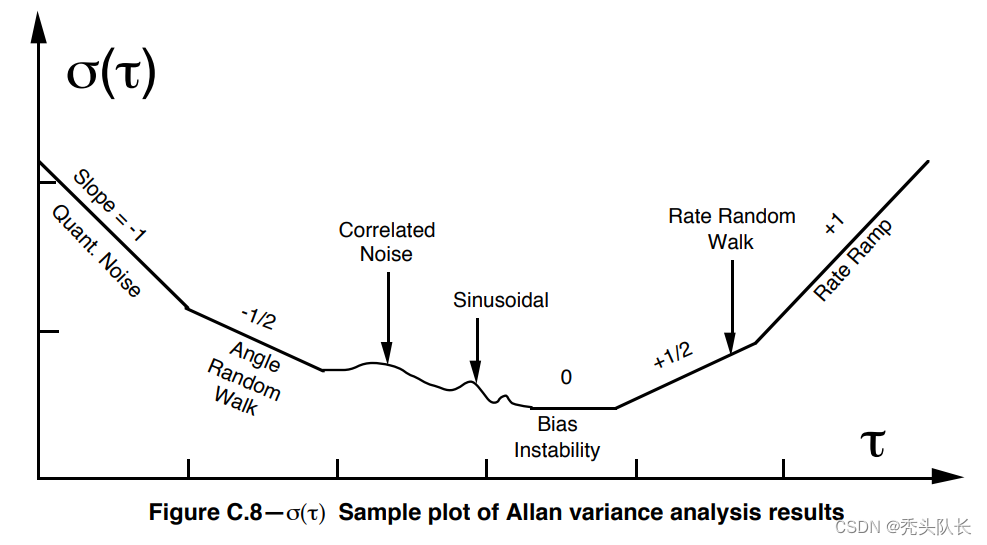
  如上图所示，如果我们计算艾伦方差，我们可以看在在图的左侧$\tau =1$以及拟合-1/2斜率这条线，以获得传感器的白噪声。类似地，可以评估右侧$\tau =3$ 以及1/2 斜率的这条线以获得随机游走噪声。我们有一个可以在 matlab 中做到这一点的包，但实际的验证和转换为C++代码库尚未完成。请参阅我们的 kalibr_allan github 项目，详细了解如何为传感器生成此图并计算值。请注意，可能需要将计算值膨胀 10-20 倍才能获得可用的传感器值。

动态 IMU 摄像头标定（离线）
  在获得相机和IMU的内参后，我们现在可以对两个传感器之间的变换进行动态校准。为此，我们再次利用 Kalibr 标定工具箱。对于这些收集的数据集，重要的是尽量减少相机中的运动模糊，同时确保激励IMU的所有轴。需要至少有一个平移运动以及两个方向变化才能观察到这些标定参数（请参阅我们最近的论文：使用在线空间和时间传感器标定的辅助INS的简并运动分析）。我们建议尽可能多地改变方向，以确保收敛。

1. 下载并构建 Kalibr 工具箱。
2. 打印出要使用的标定板（我们通常使用 Aprilgrid 6x6 0.8x0.8米）。
3. 确保传感器驱动程序使用正确的时间戳发布到 ROS 上。
4. 传感器准备。
   ● 通过减少曝光时间来限制运动模糊;
   ● 以高帧率 （20-30hz） 发布;
   ● 以合理的速率（200-500hz）发布惯性读数;
5. 录制 ROS 数据包，并确保可以从不同的方向，距离看到标定板，并且大部分在图像的中心。您应该以平滑的非生涩运动移动，其轨迹可以同时激发尽可能多的方向和平移方向。30-60秒的数据集通常足以进行标定。
6. 最后运行校准。
   ● 使用kalibr_calibrate_imu_camera
   ● 输入您的静态标定文件，其中将包含相机话题
   ● 您需要使用噪声参数创建一个 imu.yaml 文件。
   ● 根据数据集中的帧数，这可能需要半天以上的时间。
7. 检查最终结果。您需要确保拟合到惯性读数的样条已正确拟合。确保您的估计偏差不会超出您的 3-sigma 界限。否则说明你的轨迹太动态了，或者你的噪声值不好。使用手动测量值检查您的最终旋转和平移。

---

2. IMU Propagation Derivations

2.1 IMU Measurements
  我们使用 6 轴惯性测量单元 （IMU） 来传播惯性导航系统 （INS），该系统提供局部旋转速度(角速率) ${\omega }_m$和局部平移加速度${\alpha }_m$的测量：
$${\omega }_m(t)=\omega (t)+b_g(t)+n_g(t)$$$${\alpha }_m(t)=\alpha (t)+{}_G^{I}R(t{)}_g^G+b_a(t)+n_a(t)$$
其中 $\omega$ 和 $\alpha$ 是 IMU 本地坐标系 { I } \{I\} {I}中的真实旋转速度和平移加速度，$b_g$ 和 $b_a$ 是陀螺仪和加速度计偏差，$n_g$ 和 $n_a$ 是白高斯噪声，${}^{G}g={\left[\begin{array}{ccc}0& 0& 9.81\end{array}\right]}^{\top }$ 是全局坐标系 { G } \{G\} {G}中表示的重力（注意重力在地球的不同位置略有不同），${}_G^{I}R$是从全局坐标系到 IMU 本地坐标系的旋转矩阵。

2.2 State Vector
  我们将 INS 在时间 $t$ 的状态向量 $X_I$ 定义为：
$$X_I(t)=\left[\begin{array}{c}{}_G^I\bar{q}(t)\\ {}^G{p}_I(t)\\ {}^G{v}_I(t)\\ b_g(t)\\ b_a(t)\end{array}\right]$$

其中，单位四元数 ${}_G^I\bar{q}$ 表示 IMU 帧的旋转全局，${}^G{p}_I$ 是 IMU 在全局帧中的位置，${}^G{v}_I$ 是 IMU 在全局帧中的速度。为了表示清晰起见，我们通常会将时间写成描述当时 IMU 状态的下标（例如 ${}_G^{I_t}\bar{q}={}_G^I\bar{q}(t)$）。为了定义 IMU 误差状态，对位置、速度和偏差采用标准的加性误差定义，而我们使用具有左四元数乘法误差 $\otimes$ 的四元数误差状态 $\delta \bar{q}$:
$${}_G^I\bar{q}=\delta \bar{q}\otimes {}_G^I\hat{\bar{q}}$$$$\delta \bar{q}=\left[\begin{array}{c}\hat{k}sin(\frac{1}{2}\tilde{\theta })\\ cos(\frac{1}{2}\tilde{\theta })\end{array}\right]\approx \left[\begin{array}{c}\widehat{\frac{1}{2}}\tilde{\theta }\\ 1\end{array}\right]$$
其中 $\hat{k}$ 是旋转轴，$\tilde{\theta }$ 是旋转角度，对于小旋转，误差角度矢量近似为 $\tilde{\theta }=\tilde{\theta }\hat{k}$，作为关于三个方向轴的误差向量。因此，全部 IMU 误差状态定义为以下 15x1（非 16x1）矢量：
$${\tilde{X}}_I(t)=\left[\begin{array}{c}{}_G^I\tilde{\theta }(t)\\ {}^G{\tilde{p}}_I(t)\\ {}^G{\tilde{v}}_I(t)\\ {\tilde{b}}_g(t)\\ {\tilde{b}}_a(t)\end{array}\right]$$

2.3 IMU Kinematics
IMU 状态随时间演变如下（参见用于 3D 姿态估计的间接卡尔曼滤波）。
$${}_G^I\dot{\bar{q}}(t)=\frac{1}{2}\left[\begin{array}{cc}-\omega (t)\times & \omega (t)\\ -{\omega }^{\top }(t)& 0\end{array}\right]{}_G^{I_t}\bar{q}$$$$=:\frac{1}{2}\Omega (\omega (t)){}_G^{I_t}\bar{q}$$$${}^G{\dot{p}}_I(t)={}^G{v}_I(t)$$$${}^G{\dot{v}}_I(t)={}_G^{I_t}{R}^{\top }a(t)$$$${\dot{b}}_g(t)=n_{\omega g}$$$${\dot{b}}_a(t)=n_{\omega a}$$

  我们将陀螺仪和加速度计偏差建模为随机游走，因此它们的时间导数是高斯白噪声（高斯白噪声中的高斯是指概率分布是正态函数，而白噪声是指它的二阶矩不相关，一阶矩为常数，是指先后信号在时间上的相关性。）。请注意，上述运动学是根据真实加速度和角速度定义的。

---

3. First-Estimate Jacobian Estimators

3.1 EKF 线性化误差状态系统
  在开发扩展卡尔曼滤波器（EKF）时，需要围绕某个线性化点对非线性运动和测量模型进行线性化。这种线性化是导致估计误差不准确的误差来源之一（除了模型误差和测量噪声之外）。让我们考虑以下线性化误差状态视觉惯性系统：
$${\tilde{X}}_{k|k-1}={\Phi }_{(k.k-1)}{\tilde{X}}_{k-1|k-1}+G_k{w}_k$$$${\tilde{Z}}_k=H_k{\tilde{X}}_{k|k-1}+n_k$$
其中状态包含惯性导航状态和单个环境特征（请注意，我们不包括偏差以简化推导）：
$$X_k={\left[\begin{array}{cccc}{}_G^{I_k}{\bar{q}}^{\top }& {}^G{p}_{I_k}^{\top }& {}^G{v}_{I_k}^{\top }& {}^G{p}_f^{\top }\end{array}\right]}^{\top }$$
  请注意，我们使用左四元数误差状态（有关详细信息，请参见用于3D姿态估计的间接卡尔曼滤波器）。为简单起见，我们假设相机和 IMU 帧相同的转换。我们可以根据第 $k$ 个时间步长的透视投影相机模型计算给定特征的雅可比测量值，如下所示：
$$H_k=H_{proj,k}{H}_{state,k}$$$$=\left[\begin{array}{ccc}\frac{1}{I_Z}& 0& \frac{{}^{\_I}x}{({}^{I}z{)}^2}\\ 0& \frac{1}{{}^{I}z}& \frac{{}^{\_I}y}{({}^{I}z{)}^2}\end{array}\right]\left[\begin{array}{cccc}\lfloor {}_G^{I_k}R({}^G{p}_f-{}^G{p}_{I_k})\times \rfloor & -{}_G^{I_k}R& 0_{3\times 3}& {}_G^{I_K}R\end{array}\right]$$$$=H_{proj,k}{}_G^{I_k}R\left[\begin{array}{cccc}\lfloor ({}^G{p}_f-{}^G{p}_{I_k})\times \rfloor {}_G^{I_k}{R}^{\top }& -I_{3\times 3}& 0_{3\times 3}& I_{3\times 3}\end{array}\right]$$
  从时间步长 $k-1$ 到 $k$ 的状态转换（或系统雅可比矩阵）作为（有关更多详细信息，请参阅 IMU 传播推导）：
$${\Phi }_{(k,k-1)}=\left[\begin{array}{cccc}{}_{I_{k-1}}^{I_k}R& 0_{3\times 3}& 0_{3\times 3}& 0_{3\times 3}\\ -{}_G^{I_{k-1}}{R}^{\top }\lfloor \alpha (k,k-1)\times \rfloor & I_{3\times 3}& (t_k-t_{k-1}{I}_{3\times 3}& 0_{3\times 3})\\ -{}_G^{I_{k-1}}{R}^{\top }\lfloor \beta (k,k-1)\times \rfloor & 0_{3\times 3}& I_{3\times 3}& 0_{3\times 3}\\ 0_{3\times 3}& 0_{3\times 3}& 0_{3\times 3}& I_{3\times 3}\end{array}\right]$$$$\alpha (k,k-1)={\int }_{t_{k-1}}^k{\int }_{t_{k-1}}^s{}_{\tau }^{I_{k-1}}R(\alpha (\tau )-b_a-w_a)d\tau ds$$$$\beta (k,k-1)={\int }_{t_{k-1}}^{t_k}{}_{\tau }^{I_{k-1}}R(\alpha (\tau )-b_a-w_a)d\tau$$

  其中，$\alpha (\tau )$是时间 $\tau$ 的真实加速度，${}_{I_{k-1}}^{I_k}R$使用陀螺仪角速度测量计算，并且 ${}^{G}g$ 是全局参考系中的重力。在传播过程中，需要使用解析积分或数值积分来解决这些积分，而我们在这里对状态如何演变感兴趣，以便检查其可观测性。

3.2 线性化系统可观测性
  该线性化系统的可观测性矩阵由下式定义：
$$\mathcal{O}=\left[\begin{array}{c}{H}_0{\Phi }_{(0,0)}\\ H_1{\Phi }_{(1,0)}\\ H_2{\Phi }_{(2,0)}\\ ⋮\\ H_k{\Phi }_{(k,0)}\end{array}\right]$$

  其中，$H_k$是时间步长 $k$ 处的雅可比测量值，${\Phi }_{(k,0)}$是从时间步长 $0$ 到 $k$ 的复合状态转换（系统雅可比矩阵）。对于此矩阵的给定块行，我们有：
$$H_k{\Phi }_{(k,0)}=H_{proj,k}{}_G^{I_k}R\left[\begin{array}{cccc}{\Gamma }_1& {\Gamma }_2& {\Gamma }_3& {\Gamma }_4\end{array}\right]$$
$${\Gamma }_1=\lfloor {(}^G{p}_f{-}^G{p}_{I_k}{+}_G^{I_0}{R}^{\top }\alpha (k,0))\times {\rfloor }_G^{I_0}{R}^{\top }$$$${\Gamma }_2=-I_{3\times 3}$$$${\Gamma }_3=-(t_k-t_0)I_{3\times 3}$$$${\Gamma }_4=I_{3\times 3}$$

  我们现在验证以下零空间，它对应于关于重力和全局 IMU 和特征位置的全局偏航：
$$\mathcal{N}=\left[\begin{array}{cc}{}_G^{I_0}R{}^{G}g& 0_{3\times 3}\\ -{\lfloor }^G{p}_{I_0}{\rfloor }^{G}g& I_{3\times 3}\\ -{\lfloor }^G{v}_{I_0}{\rfloor }^{G}g& 0_{3\times 3}\\ -{\lfloor }^G{p}_f{\rfloor }^{G}g& I_{3\times 3}\end{array}\right]$$

  验证 $H_k{\Phi }_{(k,0)}{\mathcal{N}}_{vio}=0$ 这一点并不困难。因此，这是系统的零空间，这清楚地表明视觉惯性系统有四个不可观测的方向（全局偏航和位置）。

3.3 First Estimate Jacobians
  First-Estimate Jacobains（FEJ）方法的主要思想是确保在正确的线性化点评估状态转移和雅可比矩阵，以便上述可观测性分析成立。对于那些对技术细节感兴趣的人，请查看：8 和 13。让我们首先考虑一个关于标准卡尔曼滤波器如何计算其状态转移矩阵的小思想实验。从时间步长 $0$ 到 $1$，它将使用从状态零向前移动的当前估计值。在它使用来自其他传感器的测量值更新状态后的下一个时间步长，它将使用更新的值计算状态转换，以将状态演变为时间步长 2。这会导致状态转移矩阵的“连续性”不匹配，当按顺序乘法时，应表示从时间 $0$ 到时间 $2$ 的演变。
$${\Phi }_{(k+1,k-1)}(x_{k+1|k},x_{k-1|k-1})\ne {\Phi }_{(k+1,k)}(x_{k+1|k},x_{k|k}){\Phi }_{(k,k-1)}(x_{k|k-1},x_{k-1|k-1})$$
  如上所示，我们希望计算从所有 $k-1$ 时间处的$k-1$的测量值 ，到当前传播时间$k+1$处的所有 $k$ 的测量值的的状态转换矩阵。上述等式的右侧是人们通常在卡尔曼滤波器框架中执行此操作的方式。 ${\Phi }_{(k,k-1)}(x_{k|k-1},x_{k-1|k-1})$对应于从 $k-1$ 更新时间传播到 $k$ 时间。然后，通常会对状态执行第 $k$ 次更新，然后从此更新状态传播到最新的时间（即状态转换矩阵）。这显然与计算从时间 $k-1$ 到 $k+1$ 时间的状态转换不同，因为第二个状态转换在不同的线性化点进行评估！为了解决这个问题，我们可以更改我们评估这些的线性化点：
$${\Phi }_{(k+1,k-1)}(x_{k+1|k},x_{k-1|k-1})={\Phi }_{(k+1,k)}(x_{k+1|k},x_{k|k-1}){\Phi }_{(k,k-1)}(x_{k|k-1},x_{k-1|k-1})$$
  我们还需要确保我们的测量雅可比量与状态转移矩阵的线性化点相匹配。因此，它们也需要在$x_{k|k-1}$线性化点进行评估，而不是通常使用的$x_{k|k}$线性化点。这种方式名为FEJ，因为我们将在同一线性化点评估雅可比矩阵，以确保零空间保持有效。

---