一、层次分析法的基本原理与步骤
人们在进行社会的、经济的以及科学管理领域问题的系统分析中，面临的常常是
一个由相互关联、相互制约的众多因素构成的复杂而往往缺少定量数据的系统。层次
分析法为这类问题的决策和排序提供了一种新的、简洁而实用的建模方法。
运用层次分析法建模，大体上可按下面四个步骤进行：
（
i
）建立递阶层次结构模型；
（
ii
）构造出各层次中的所有判断矩阵；
（
iii
）层次单排序及一致性检验；
（
iv
）层次总排序及一致性检验。
下面分别说明这四个步骤的实现过程。
1.1
递阶层次结构的建立与特点
应用
AHP
分析决策问题时，首先要把问题条理化、层次化，构造出一个有层次
的结构模型。在这个模型下，复杂问题被分解为元素的组成部分。这些元素又按其属
性及关系形成若干层次。上一层次的元素作为准则对下一层次有关元素起支配作用。
这些层次可以分为三类：
（
i
）最高层：这一层次中只有一个元素，一般它是分析问题的预定目标或理想结
果，因此也称为目标层。
（
ii
）中间层：这一层次中包含了为实现目标所涉及的中间环节，它可以由若干
个层次组成，包括所需考虑的准则、子准则，因此也称为准则层。
（
iii
）最底层：这一层次包括了为实现目标可供选择的各种措施、决策方案等，
因此也称为措施层或方案层。
递阶层次结构中的层次数与问题的复杂程度及需要分析的详尽程度有关，一般地
层次数不受限制。每一层次中各元素所支配的元素一般不要超过
9
个。这是因为支配
的元素过多会给两两比较判断带来困难。
下面结合一个实例来说明递阶层次结构的建立
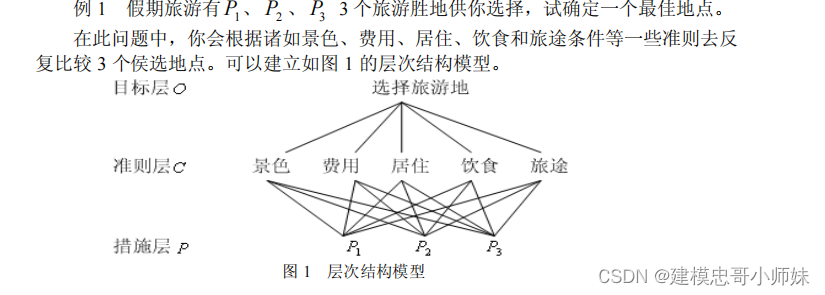
二、构造判断矩阵
层次结构反映了因素之间的关系， 但准则层中的各准则在目标衡量中所占的比重 并不一定相同，在决策者的心目中，它们各占有一定的比例。
在确定影响某因素的诸因子在该因素中所占的比重时， 遇到的主要困难是这些比 重常常不易定量化。此外， 当影响某因素的因子较多时， 直接考虑各因子对该因素有 多大程度的影响时， 常常会因考虑不周全、顾此失彼而使决策者提出与他实际认为的 重要性程度不相一致的数据，甚至有可能提出一组隐含矛盾的数据。为看清这一点， 可作如下假设：将一块重为 1 千克的石块砸成n 小块，你可以精确称出它们的重量， 设为 w1 , … , wn ，现在，请人估计这 n 小块的重量占总重量的比例（不能让他知道各 小石块的重量），此人不仅很难给出精确的比值，而且完全可能因顾此失彼而提供彼 此矛盾的数据。
设现在要比较n 个因子X = {x1 , … , xn } 对某因素Z 的影响大小， 怎样比较才能提 供可信的数据呢？ Saaty 等人建议可以采取对因子进行两两比较建立成对比较矩阵的 办法。即每次取两个因子xi 和xj ，以 aij 表示xi 和xj 对Z 的影响大小之比， 全部比较 结果用矩阵 A = (aij )n ×n 表示，称 A 为Z − X 之间的成对比较判断矩阵（简称判断矩 阵）。容易看出，若xi 与xj 对Z 的影响之比为aij ，则 xj 与xi 对Z 的影响之比应为
从心理学观点来看，分级太多会超越人们的判断能力，既增加了作判断的难度，
又容易因此而提供虚假数据。
Saaty
等人还用实验方法比较了在各种不同标度下人们判
断结果的正确性，实验结果也表明，采用
1~9
标度最为合适。最后，应该指出，一般地作
n(
n −1)/2
次两两判断是必要的。有人认为把所有元素 都和某个元素比较，即只作n
−
1
次比较就可以了。这种作法的弊病在于，任何一个判 断的失误均可导致不合理的排序，而个别判断的失误对于难以定量的系统往往是难以 避免的。进行
n
(
n
−
1)/2次比较可以提供更多的信息，通过各种不同角度的反复比较， 从而导出一个合理的排序.
三、层次单排序及一致性检验
四、层次总排序及一致性检验
五、层次分析法的应用
在应用层次分析法研究问题时，遇到的主要困难有两个：（
i
）如何根据实际情况
抽象出较为贴切的层次结构；（
ii
）如何将某些定性的量作比较接近实际定量化处理。
层次分析法对人们的思维过程进行了加工整理，提出了一套系统分析问题的方法，为
科学管理和决策提供了较有说服力的依据。但层次分析法也有其局限性，主要表现在：
（
i
）它在很大程度上依赖于人们的经验，主观因素的影响很大，它至多只能排除思维
过程中的严重非一致性，却无法排除决策者个人可能存在的严重片面性。（
ii
）比较、
判断过程较为粗糙，不能用于精度要求较高的决策问题。
AHP
至多只能算是一种半定
量（或定性与定量结合）的方法。
在应用层次分析法时，建立层次结构模型是十分关键的一步。现再分析一个实例， 以便说明如何从实际问题中抽象出相应的层次结构。
例
2
挑选合适的工作。经双方恳谈，已有三个单位表示愿意录用某毕业生。该生根据已有信息建立了一个层次结构模型，如图 2
所示。
根据层次总排序权值，该生最满意的工作为工作
1
。
计算的
Matlab
程序如下：
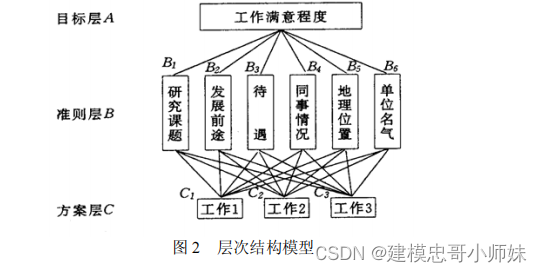
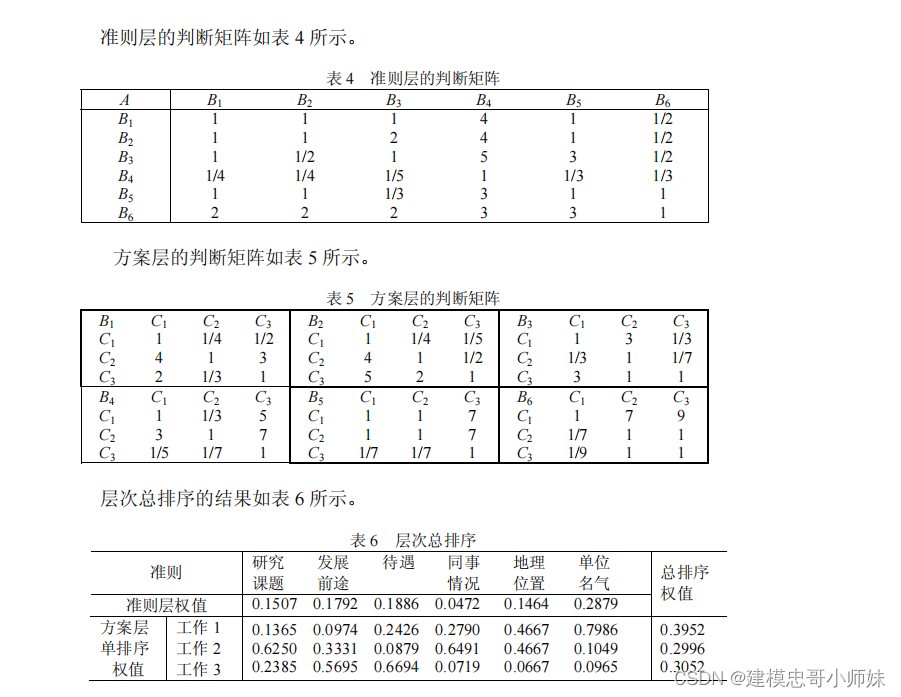
clc,clear
fid=fopen('txt3.txt','r');
n1=6;n2=3;
a=[];
for i=1:n1
tmp=str2num(fgetl(fid));
a=[a;tmp]; %读准则层判断矩阵
end
for i=1:n1
str1=char(['b',int2str(i),'=[];']);
str2=char(['b',int2str(i),'=[b',int2str(i),';tmp];']);
eval(str1);
for j=1:n2
tmp=str2num(fgetl(fid));
eval(str2); %读方案层的判断矩阵
end
end
ri=[0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45]; %一致性指标
[x,y]=eig(a);
lamda=max(diag(y));
num=find(diag(y)==lamda);
w0=x(:,num)/sum(x(:,num));
cr0=(lamda-n1)/(n1-1)/ri(n1)
for i=1:n1
[x,y]=eig(eval(char(['b',int2str(i)])));
lamda=max(diag(y));
num=find(diag(y)==lamda);
w1(:,i)=x(:,num)/sum(x(:,num));
cr1(i)=(lamda-n2)/(n2-1)/ri(n2);
end
cr1, ts=w1*w0, cr=cr1*w0
